物理 基础数据结构之图
图
〇、返回
一、图的基本概念
警察捉小偷大家都玩过吧,其实画的地图就是这里提到的“图”
1. 顶点(Vertex)
定义:图中的每个节点称为顶点。
表示:通常用字母、数字或其他符号来标识。
2. 边(Edge)
定义:连接两个顶点的路径称为边。
类型:
无向边:没有方向的边,表示两个顶点之间的关系是对称的。
有向边:具有方向的边,表示从一个顶点指向另一个顶点的关系是非对称的。
3. 图的分类
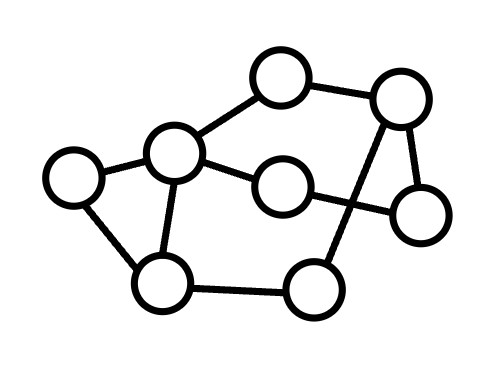
无向图:所有边都是无向边的图。
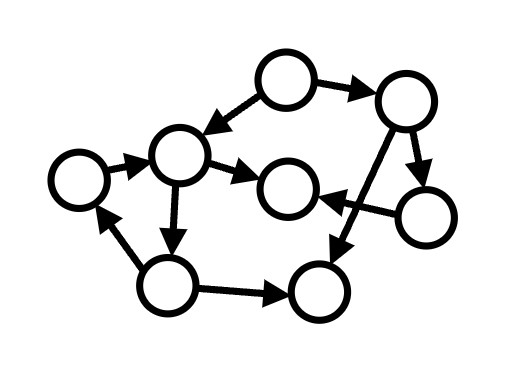
有向图:所有边都是有向边的图。
混合图:包含无向边和有向边的图。
二、图的相关术语
1. 度(Degree)
定义:一个顶点的度是指与该顶点相关联的边的数量。
无向图:顶点的度是与该顶点相连的边的数量。
有向图:
入度:指向该顶点的边的数量。
出度:从该顶点指出的边的数量。
2. 路径(Path)
定义:图中从一个顶点到另一个顶点的顶点序列。
简单路径:路径中不包含重复的顶点。
3. 连通性(Connectivity)
无向图:
连通图:任意两个顶点之间都存在路径。
连通分量:无向图中的极大连通子图。
有向图:
强连通图:任意两个顶点之间都存在双向路径。
弱连通图:将有向边视为无向边后形成的无向图是连通的。
4. 环(Cycle)
定义:起点和终点相同的路径。
简单环:除起点和终点外,不包含重复顶点的环。
自环:一条边的两边都指向同一个节点
三、图的存储结构
1. 邻接矩阵(Adjacency Matrix)
定义:使用一个二维数组来表示图中顶点之间的连接关系。
特点:
空间复杂度为O($V^2$),其中V是顶点的数量。
适用于稠密图(边的数量接近$V^2$)。
2. 邻接表(Adjacency List)
定义:使用链表来存储每个顶点的邻接顶点。
特点:
空间复杂度为O(V+E),其中E是边的数量。
适用于稀疏图(边的数量远小于$V^2$)。
四、图的常见操作
1. 图的遍历
深度优先搜索(DFS):从某个顶点出发,尽可能深入地访问相邻顶点。
广度优先搜索(BFS):从某个顶点出发,逐层访问相邻顶点。
2. 最短路径
Dijkstra算法:用于找到单源最短路径(适用于非负权图)。
Floyd算法:用于找到所有顶点对之间的最短路径。
3. 最小生成树
Prim算法和Kruskal算法:用于找到无向连通图的最小生成树。
注:上述算法在后面都会讲到
五、图的应用
网络路由:互联网中的路由选择。
社交网络分析:分析用户之间的关系。
任务调度:项目管理中的任务依赖关系。
地图导航:寻找最短路径。
