哈夫曼树

〇、返回

返回传送门

一、基本概念

哈夫曼树（Huffman Tree），又称最优二叉树，是一种带权路径长度最短的二叉树。也就是说，对于给定的一组权值，可以构造出若干棵二叉树，其中带权路径长度（WPL）最小的二叉树即为哈夫曼树。

路径

从树中一个节点到另一个节点之间的分支构成这两个节点之间的路径。

路径长度

路径上的分支数目。

节点的权

将树中节点赋予一个表示某种意义的数值，则这个数值称为该节点的权。

节点的带权路径长度

从根节点到该节点之间的路径长度与该节点的权的乘积。

树的带权路径长度（WPL）

树中所有叶子节点的带权路径长度之和。

二、哈夫曼树的定义

给定n个权值作为n个叶子节点，构造一棵二叉树，若该树的带权路径长度（WPL）达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树。

三、哈夫曼树的构造

哈夫曼提出了一个构造最优二叉树的算法，其基本思想如下：

初始化：根据给定的n个权值{w1, w2, ..., wn}构造n棵二叉树的集合F={T1, T2, ..., Tn}，其中每棵二叉树Ti中只有一个权值为wi的根节点，左右子树均为空。

构造过程：

    在F中选取两棵根节点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根节点的权值为其左右子树上根节点的权值之和；

    在F中删除这两棵树，同时将新得到的二叉树加入F中；

    重复以上两步，直到F只含一棵树为止，这棵树便是哈夫曼树。

四、哈夫曼树的性质

1. 哈夫曼树中没有度为1的节点。

2. 对于具有n个叶子节点的哈夫曼树共有2n-1个节点。

3. 若初始森林中有n棵树（即n个叶子节点），则要经过n-1次合并，最后才得到一棵哈夫曼树。

五、哈夫曼编码

哈夫曼树的一个重要应用是用于信息的编码。在数据通信中常采用二进制编码来表示字符。如果对每个字符都用相同长度的二进制位来编码，则称为等长编码；如果允许对不同字符用不等长的二进制位来编码，则称为变长编码。

利用哈夫曼树可以设计出变长编码，这种编码称为哈夫曼编码。具体方法如下：

    将n个字符作为n个叶子节点，其权值为各字符在电文中出现的频率或次数。

    构造一棵哈夫曼树。

    规定哈夫曼树中的左分支代表0，右分支代表1，则从根节点到每个叶子节点所经过的路径分支组成的0和1的序列便为该节点对应字符的编码。

六、示例

假设需要对四个字符A、B、C、D进行编码，它们的权值分别为7、5、2、4。

1. 初始化

    创建四个节点，权值分别为7、5、2、4。

2. 第一次合并

    选择权值为2和4的两个节点合并，形成一个新的节点，权值为6。

3. 第二次合并

    选择权值为5和6的两个节点合并，形成一个新的节点，权值为11。

4. 第三次合并

    选择权值为7和11的两个节点合并，形成最终的哈夫曼树，根节点权值为18。

最终得到的哈夫曼树如下（假设左子树为0，右子树为1）：

        18

        /  \

       7  11

           /  \

          5   6

              /  \

             2   4

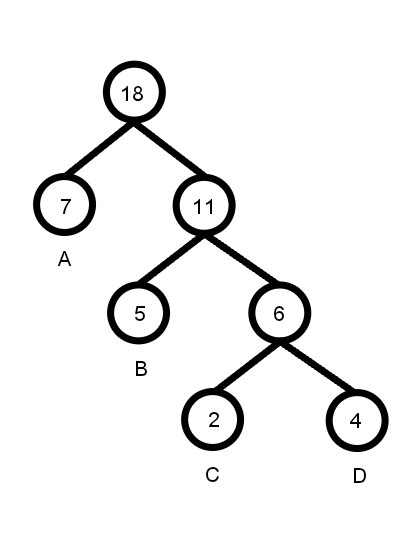
根据这棵树，可以得到每个字符的哈夫曼编码：

A: 0

B: 10

C: 110

D: 111

七、总结

哈夫曼树在数据压缩、编码等领域有广泛的应用，其核心思想是通过构造最优二叉树来实现最短的加权路径长度，从而达到最优的编码效果。