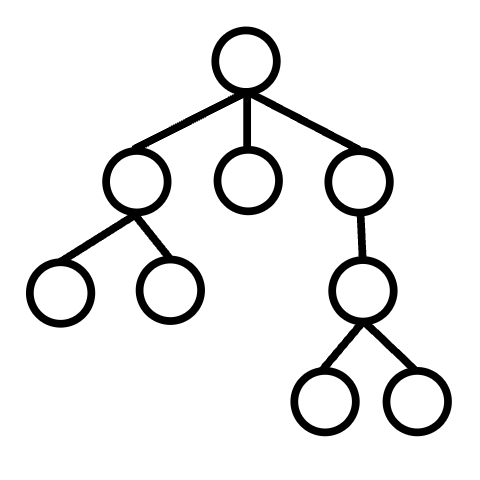
二、树的基本术语

节点

树中的一个独立单元，包含一个数据元素及若干指向其子树的分支。

根节点

一棵树中唯一一个没有父节点的节点

叶子节点

没有子节点的节点。

父节点

如果有向边A->B，则称A为B的父节点。

子节点

如果有向边A->B，则称B为A的子节点。

兄弟节点

具有同一父节点的各节点彼此是兄弟节点。

路径和路径长度

从节点n1到nk的路径为一个节点序列n1, n2, ..., nk，ni是ni+1的父节点。路径所包含边的个数为路径的长度。

节点的度

节点拥有的子树个数称为节点的度。

树的度

树内各节点的度的最大值。

深度（或高度）

节点的深度是从根节点到该节点的唯一路径上的边的数量；树的高度是指树中节点的最大深度。

森林

多棵互不相交的树的集合。

三、树的存储结构

树的存储结构主要有两种：双亲表示法、孩子表示法和孩子兄弟表示法。

双亲表示法

用一组连续的存储单元来存储树的节点，并在每个节点中附设一个指示器指示其父节点的位置。

孩子表示法

将每个节点的孩子节点用单链表存储，然后将这些单链表的头指针存放在一个数组中。

孩子兄弟表示法

每个节点包括三个域：数据域、第一个孩子域和右兄弟域。这种表示法可以将任意树转换为二叉树。

四、树的遍历

树的遍历是指从根节点出发，按照某种次序访问树中的所有节点，使得每个节点被访问一次且仅被访问一次。

常见的遍历方法有：

先序遍历

先访问根节点，然后依次先根遍历每个子树。

后序遍历

先依次遍历每个子树，然后访问根节点。

层序遍历

从树的根节点开始，从上到下逐层遍历，在同一层中，按从左到右的顺序进行。

五、树的应用

树在计算机科学中有广泛的应用，例如：

文件系统

操作系统中的文件目录结构可以看作是一棵树。

表达式树

用于表示算术表达式或逻辑表达式。

决策树

用于机器学习中的分类和回归问题。

组织结构图

公司或机构的组织结构可以用树来表示。

六、总结

树作为一种非线性数据结构，能够有效地表示具有层次关系的数据。理解树的基本概念、性质、存储结构和常见操作，对于解决实际问题具有重要意义。