物理 基础数据结构之栈
栈
〇、返回
一、栈的基本概念
定义
栈是一种特殊的线性数据结构,它遵循“后进先出”(LIFO, Last In First Out)的原则。这意味着最后被添加到栈中的元素将是第一个被移除的元素。
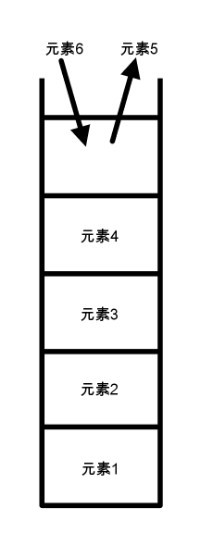
特性
单一入口
所有插入和删除操作都在栈顶进行。
顺序存储
元素按照一定的顺序存储,通常是按照它们被添加的顺序。
动态变化
栈的大小会随着元素的添加和移除而动态变化。
二、栈的操作
初始化
创建一个空栈,通常在开始使用栈之前进行。
入栈(Push)
将一个新元素添加到栈顶。这是增加栈中元素数量的操作。
出栈(Pop)
移除栈顶元素,并返回该元素的值。这是减少栈中元素数量的操作。如果栈为空,则无法进行出栈操作。
获取栈顶元素(Top)
返回栈顶元素的值,但不移除该元素。这允许你在不改变栈状态的情况下查看栈顶元素。
判断栈是否为空(Empty)
检查栈中是否没有任何元素。这是一个布尔操作,返回True如果栈为空,否则返回False。
获取栈的大小(Size)
返回栈中元素的数量。这有助于了解当前栈的状态。
三、栈的实现方式
数组实现
优点
访问速度快:由于数组支持随机访问,因此可以快速访问栈中的任意元素。
空间效率高:预先分配的空间可以有效利用。
缺点
固定大小:需要在创建时指定栈的最大容量,如果超过这个容量则会发生溢出。
空间浪费:如果实际使用的元素数量远小于预分配的空间,会造成空间浪费。
链表实现
比较复杂,这里不过多展开,了解即可
四、栈的应用场景
表达式求值和括号匹配
表达式求值
例如,计算逆波兰表达式(后缀表达式)的值。通过栈可以方便地处理运算符的优先级和操作数的顺序。
括号匹配
检查代码中的括号(如()、[]、{})是否正确配对。每遇到一个左括号就将其入栈,每遇到一个右括号就检查它是否与栈顶的左括号匹配。
函数调用和递归
函数调用
在函数调用过程中,系统使用栈来保存每一层函数调用的状态,包括局部变量、参数和返回地址等。
递归
递归算法本质上是通过栈来实现的。每次递归调用都会在栈中创建一个新的帧,保存当前状态。
回溯算法
如八皇后问题
浏览器的前进和后退功能
前进和后退用户浏览网页时,当前页面可以视为栈顶元素,后退操作相当于出栈,前进操作相当于入栈。这样可以方便地在浏览历史中来回切换。
五、栈的变种
有限栈
限定栈的最大容量,当栈满时无法再进行入栈操作。
多栈
在一个数据结构中实现多个栈,每个栈独立管理自己的元素。
栈队列
使用两个栈来模拟队列的行为,实现先进先出(FIFO)的操作。
六、总结
栈是一种非常基础且重要的数据结构,广泛应用于各种算法和实际问题中。理解栈的工作原理和应用场景,可以帮助你更好地设计和优化程序。栈的简单性和高效性使其成为解决许多问题的理想选择。
