物理 Look!是一筐半湿不干的干货(#数学篇)
本帖适用人群:小学~初中生(预备轮及以下)实则就是主播肝完预备轮之后的总结,当然也有一些中考压轴题
由于本帖的学术指标不够格,所以只是普通的学术帖,并不在obox专区,但也希望大家不要水评论,保持本帖良好的环境,同时主播也会继续学习新知识,争取有朝一日发上真正的竞赛学术帖
目前进度:未完结
——————
Part 1 代数合集
常见因式分解:一提,二代,三分组;十字相乘;拆添项;双十字相乘等(一提,指提取公因式;二代,指代入公式)
常用公式:$a^2-b^2=(a-b)(a+b)$
$(a±b)^2=a^2±2ab+b^2$
$a^3-b^3=(a-b)(a^2+ab+b^2)$
$a^3+b^3=(a+b)(a^2-ab+b^2)$
$(a+b)^3=a^3+3a^2b+3ab^2+b^3$
$(a-b)^3=a^3-3a^2b+3ab^2-b^3$
$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$
注意看,在上面的公式中,有许多类似的式子,例如:$a^2+ab+b^2$
这个式子的每一项的次数都相等,都是二次项,我们把这样每一项次数都相同的整式称作*次齐次式,就如上面这个式子我们就叫它为二次齐次式
关于二次三项式既约的判断:(在有理数/整数的范围内)
1.$x^2+bx+c=(x+k_1)(x+k_2)$
即二次多项式=(一次因式)(一次因式)
则$k_1~k_2$为$x^2+bx+c=0$的两根
∴若∆<0,$x^2+bx+c$无法因式分解
∆≥0,也不一定因式分解,因为可能为无理根(如:$x+\frac{3±\sqrt{5}}{2}$)
2.『整系数多项式若能分解为有理数系数因式的积,则定能分解为整系数因式的积』
因式定理:当$f(c)=0$时,即$f(x)$除以$(x-c)$的余数为0
即$f(x)$能被$(x-c)$整除
即$f(x)$有一因式$(x'-c)$
轮换式与对称式:
1)对称:$x+y↔y+x$
$xy↔yx$
$x+y+xy↔y+x+yx$
常见对称:$xyz$
$x^3+y^3+z^3$
$x^2y+y^2x$
2)轮换: x
↗ ↘
z ← y
①轮换式因式分解的结果一定是轮换式的积(一定也轮换)
②每个轮换式都可以被表示为基本轮换式线性之和
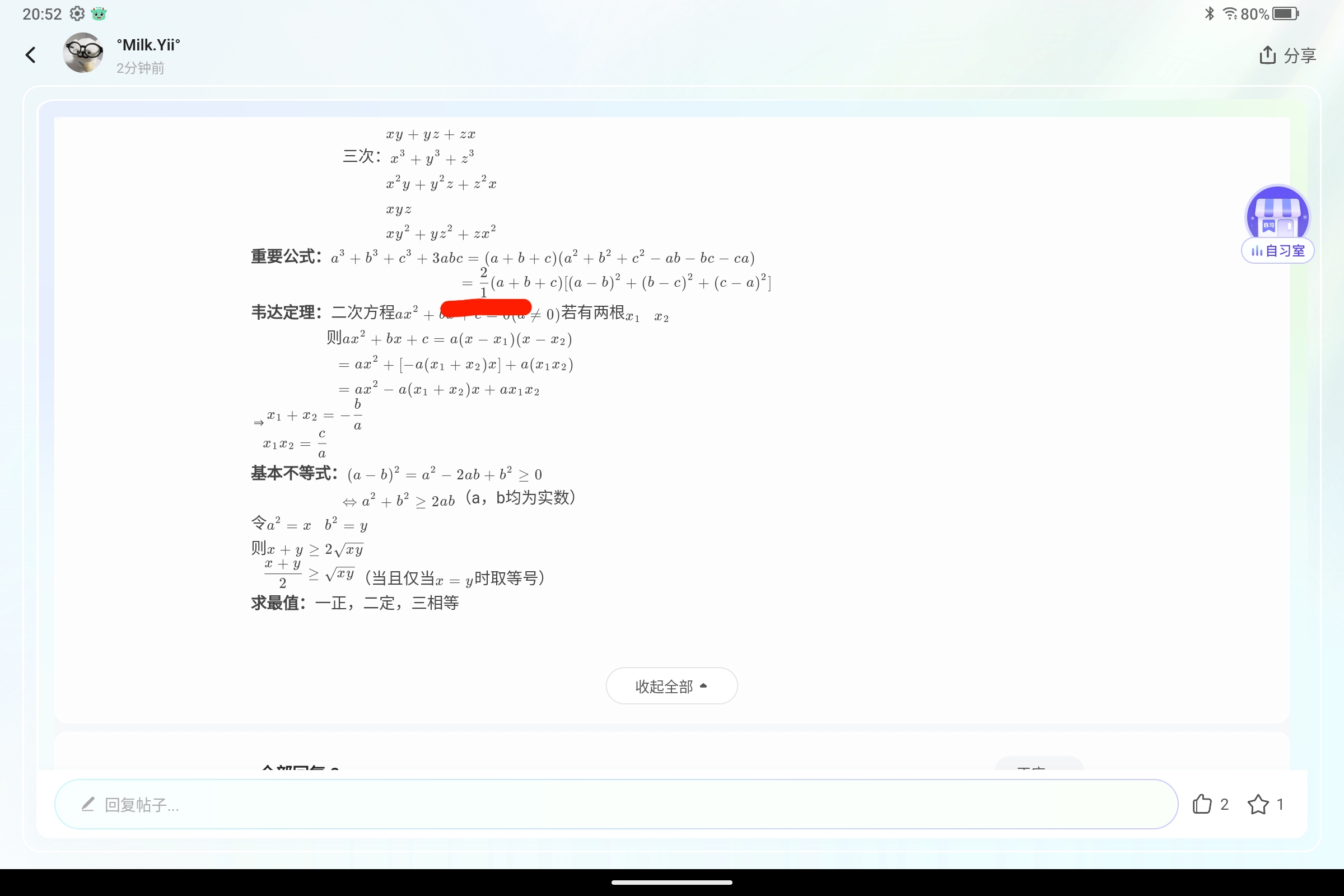
基本轮换式:一次:$x+y+z$
二次:$x^2+y^2+z^2$
$xy+yz+zx$
三次:$x^3+y^3+z^3$
$x^2y+y^2z+z^2x$
$xyz$
$xy^2+yz^2+zx^2$
重要公式:$a^3+b^3+c^3+3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$
$=\frac{1}{2}(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]$
韦达定理:二次方程$ax^2+bx+c=0(a≠0)$若有两根$x_1~~~x_2$
则$ax^2+bx+c=a(x-x_1)(x-x_2)$
$=ax^2+[-a(x_1+x_2)x]+a(x_1x_2)$
$=ax^2-a(x_1+x_2)x+ax_1x_2$
⇒$x_1+x_2=-\frac{b}{a}$
$x_1x_2=\frac{c}{a}$
基本不等式:$(a-b)^2=a^2-2ab+b^2≥0$
$⇔a^2+b^2≥2ab$(a,b均为实数)
令$a^2=x~~~b^2=y$
则$x+y≥2\sqrt{xy}$
$\frac{x+y}{2}≥\sqrt{xy}$(当且仅当$x=y$时取等号)
求最值:一正,二定,三相等
———————
Part 2 数论合集
1.整除理论:①整除式定义:对于$a,b∈z~a≠0$
⑴若存在$q∈z$,使得$b=aq~a≠0$则可称b可被a整除
记作$a|b$也称a整除b,且称b为a的倍数,a为b的因数
⑵若a不整除b,记作$a\nmid~b$
②性质:❶与正负无关:$a|b⇔a|-b$
❷传递性:$a|b~b|c⇒a|c$
❸线性组合:$a|b~a|c⇔$任意$x,y∈z$,有$a|bx+cy$
❹$m≠0,a|b⇔ma|mb$
❺$a|b,b|a⇒a=±b$
2.自然数:①最小自然数原理:有一个组成元素均为自然数的集合,则定有一个最小的自然数。
②若x为自然数,则x+1也为自然数→数学归纳法
3.质数:①定义:除0与±1之外,若p的因数只有±1和±p本身,则称该数为质数/素数(其中±1,±p被称之为“显然约数”)
②性质:⑴质数无穷
⑵只有一个偶质数2
4.合数:①定义:a为合数⇔a=de,1<d<a,1<e<a
②性质:一定拥有质数因数
5.裴蜀定理:$∃x,y∈z,ax+by=1$⇔a,b只有一个公因数为1
6.奇数偶数:①定义:$n÷2=q······r$
⑴若$r=0⇒$是偶数⇒$2|n$
⑵若$r=1⇒$是奇数⇒$2\nmid~n$
②性质:❶奇数≠偶数
❷奇数的因数均为奇数
❸奇数个奇数之和为奇数;偶数个奇数之和为偶数
❹整数+偶数奇偶性不变;整数+奇数奇偶性改变
❺整数×奇数奇偶性不变;整数×偶数则变为偶数
7.因数与倍数:①定义:$a|b$,a为b的因数,b为a的倍数
②公因数:$d|a_1,d|a_2,d|a_3······d|a_k$;d为$a_1,a_2······a_k$的公因数
③最大公因数:⑴记作$(a_1,a_2)$
⑵性质:❶$(a_1,a_2)=(a_1,-a_2)$
❷若$a_1|a_2$,则$(a_1,a_2)=|a_1|$
❸对于$∀x∈z,(a_1,a_2)=(a_1,a_2,a_1x)$
❹设$m|(a_1,a_2)$
有$m(\frac{a_1}{m},\frac{a_2}{m})=(a_1,a_2)$
共7条回复
时间正序