数学

反三角函数

反三角函数与三角方程

零、前言

我们知道道基本初等函数包括以下六种函数：

常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数。

由基本初等函数经过四则运算以及简单复合（就像平移、对称、反转等）所得的函数叫初等函数

注意：观看此帖子的朋友们至少有三角函数基础，如：诱导公式（在这个帖子会用到诱导公式）

指引：若有疑问，可以在问题楼提问，谢谢配合。

目录

第一部分 反三角函数

第二部分 三角方程

§ 第一部分 反三角函数

 一、反函数

• 设y = f(x)的定义域为D，值域为$R_f$.若对于任意$y∈R_f$都可确定唯一的$x∈D$满足$y = f(x)$，则称x为y的函数，记为$x = f^{-1}(y)$称为y=f(x)的反函数.

  $\color{red}{注：习惯上也将y = f(x)的反函数写为y = f^{-1}(x)}$

  $\color{skyblue}{并不是所有的函数都有反函数}$

  $\color{red}{函数y = f(x)与其反函数y = f^{-1}(x)的图像关于y=x对称}$

  $\color{red}{严格单调函数一定有反函数}$

  $\color{red}{反函数要求原函数是单射}$ 

  就像$y = x^3$它的反函数就是$y =\sqrt[3]{x}$

小试牛刀

[例题1] 判断下列函数是否有反函数；如果有，请求之：

本题出自《预备轮国际版AMC12综合》第一讲 第五页 例题1.4

1. $f(x) = 2x + 3$

2.$f(x) = x^2 + 1$

3.$f(x) =\sqrt{x-1}$

反函数的求法可以参考《基础轮数学A1》第141页

二、反三角函数

     1. 反三角函数存在的前提

          由于三角函数（如正弦、余弦）具有周期性和非单调性，需将其定义域限制在严格单调的区间内，在能建立一一映射关系。

      例：

• 正弦函数$y=\sin(x)$限制在$[-\frac{π}{2},\frac{π}{2}]$时单调递增，可以定义反正弦函数$\y=arcsin(x)$
• 余弦函数$y=\cos(x)$限制在$[0,π]$时单调递减，可以定义反余弦函数$y=\arccos(x)$

     2. 主值区间

         对周期性与值域受限的三角函数，将其定义域限制在严格单调且覆盖完整值域子区间，使其成为双射，该子区间称为主值区间。

     3.反三角函数本质

        反三角函数输入为三角函数值，输出为对应角度值，满足：$y=\arcsin(x)当且仅当x=\sin(y),y∈[-\frac{π}{2},\frac{π}{2}],x∈[-1,1]$其他反三角函数同理。

        [补充]:arc  /a:k/  n.弧

三、反正弦函数，$\color{red}{y=\arcsin(x)}$

      定义域：$x∈[-1,1]$

      值域：$y∈[-\frac{π}{2},\frac{π}{2}]$

      单调性：单增

      奇偶性：奇

      有界性：有界

      周期性：无

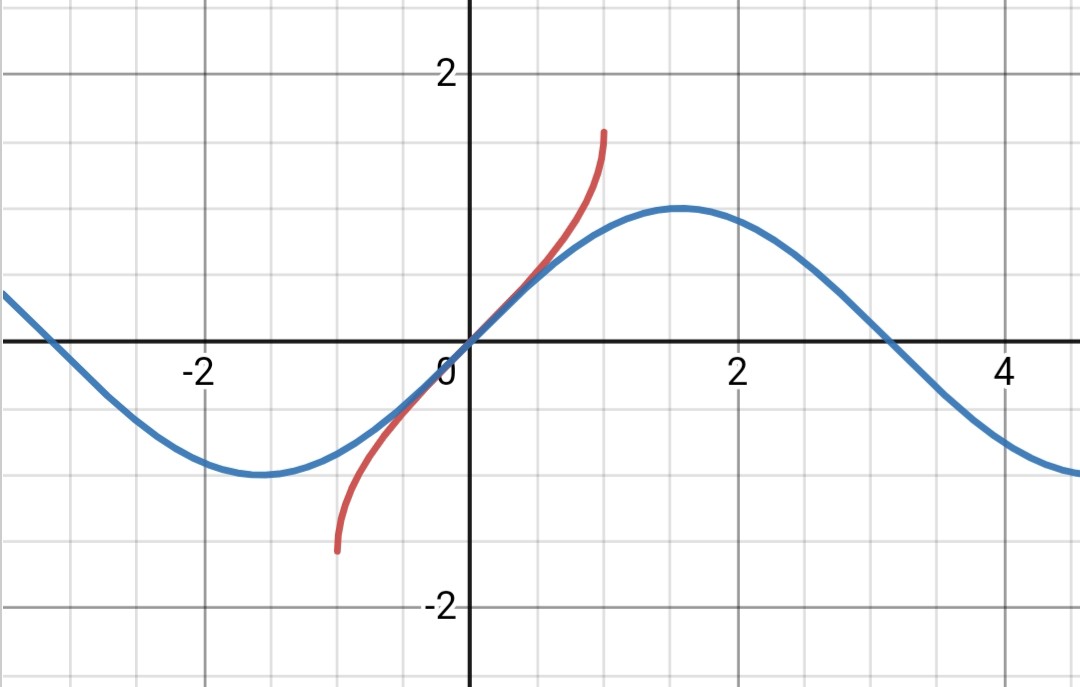
$如图为y=\sin(x)(蓝)和y=\arcsin(x)(红)的图像$

小试牛刀

[例题2]在下列式子中，有意义的为（    ）。

$[ A ].\arcsin(\sqrt{2})$.   $[ B ].\arcsin(-\frac{π}{3})$.   $[ C ].\sin(\arcsin(2))$.   $[ D ].\arcsin(\sin(2))$

②$\arcsin(\sin(a))=a,(a∈[-\frac{π}{2},\frac{π}{2}])$

[思考题]

“$y=\sin(x),x∈[\frac{π}{2},\frac{3π}{2}]的反函数是x=\arcsin(y),y∈[-1,1]$”，这个说法对吗？(本题已给出解析，见下方评论区)

四、反余弦函数，$\color{red}{y=\arccos(x)}$

      定义域：$x∈[-1,1]$

      值域：$y∈[0,π]$

      单调性：单减

      奇偶性：非奇非偶

      有界性：有界

      周期性：无

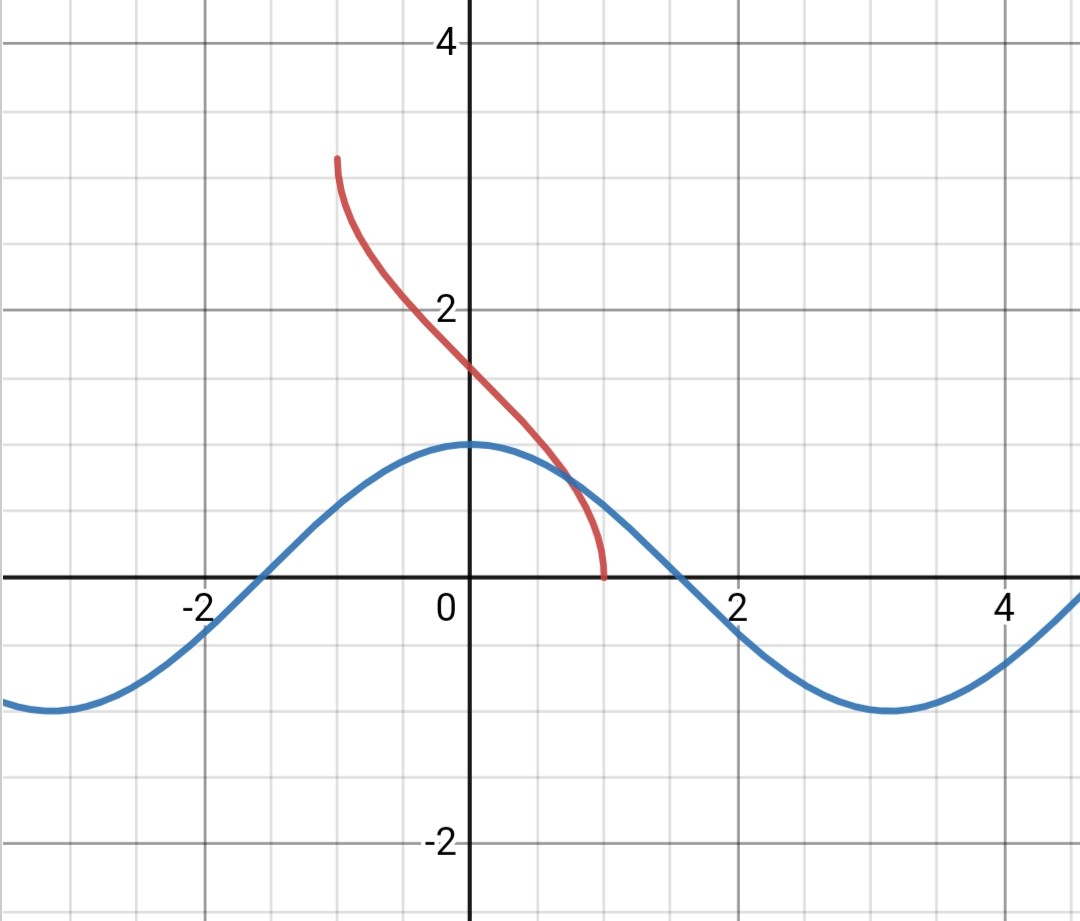
$如图为y=\cos(x)(蓝)和y=\arccos(x)(红)的图像$

小结论

①$\arccos(-x)=π-\arccos(x),x∈[-1,1].$    “互补”

②$\cos(\arccos(a))=a,a∈[-1,1];$

   $\arccos(\cos(a))=a,a∈[0,π].$

③$\arccos(x)+\arcsin(x)=\frac{π}{2},x∈[-1,1].$   “互余”

小试牛刀

[例3]计算$\arccos(\cos(\frac{11π}{6}))$=_____.

五、反正切函数，$\color{red}{y=\arctan(x)}$

      定义域：$x∈(-∞,+∞)$

      值域：$y∈(-\frac{π}{2},\frac{π}{2})$

      单调性：单增

      奇偶性：奇

      有界性：有界

      周期性：无

$如图为y=\tan(x)(蓝)和y=\arctan(x)(红)的图像$

小结论：

$\tan(\arctan{a})=a,a∈\mathbb{R}.$

$\arctan(\tan{a})=a,a∈(-\frac{π}{2},\frac{π}{2}).$

小试牛刀

[例4]$y=\arctan(\tan{x})$是否为周期函数？ (本题会给出解析)