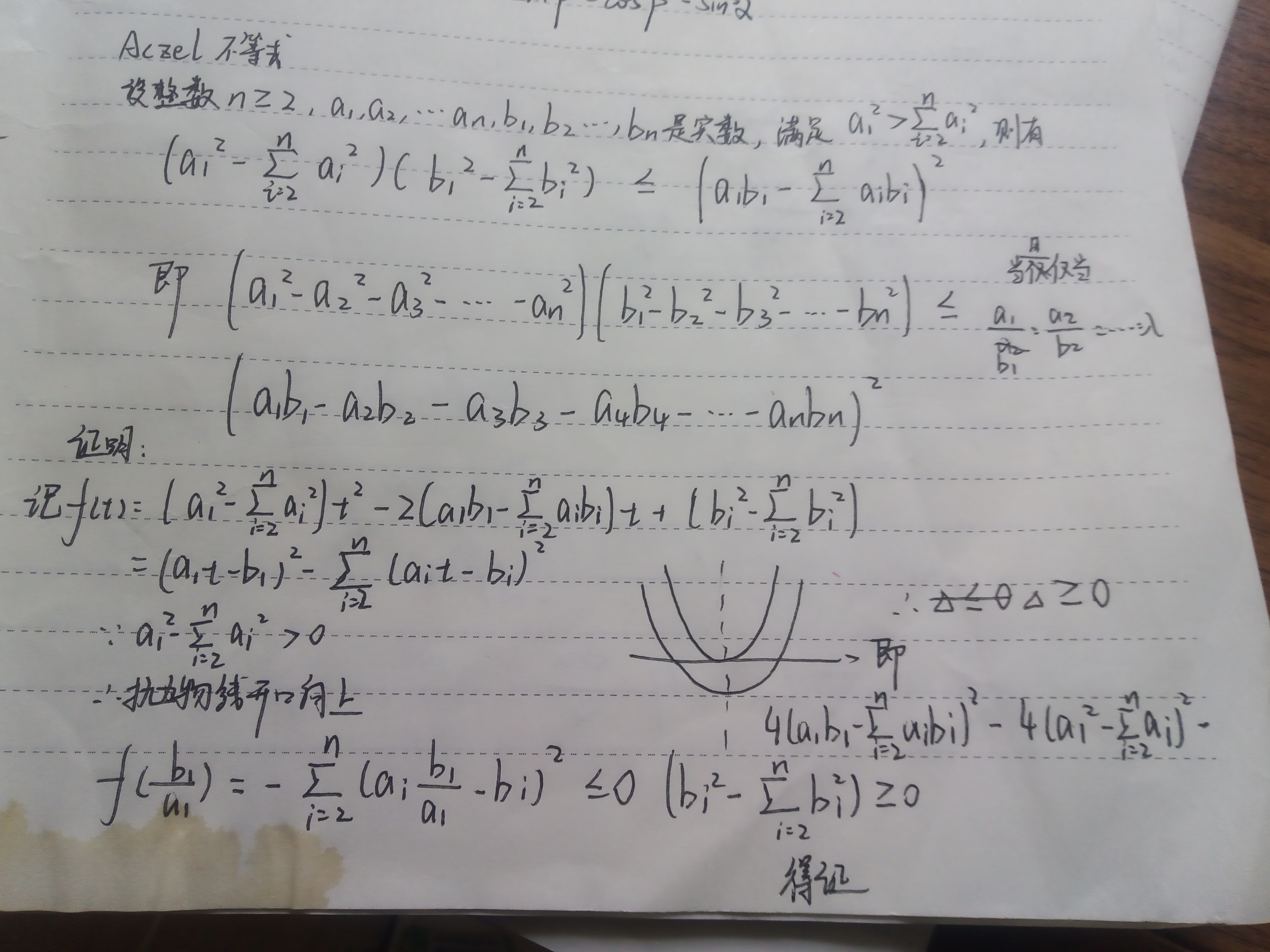数学

不等式收集

• 本帖所收录不等式可供练习，欢迎各位在评论区给出证明
• 本帖不会收录基本或常见的不等式，如Cauchy、Holder···

• 禁止无意义提问（）

1.康托洛维奇（Kantorovich）不等式

$设正实数 \lambda_1, \lambda_2, \cdots, \lambda_n $ $满足$ $\sum_{i = 1}^{n} \lambda_i = 1，$ $实数$ $0 \lt m \le a_{i} \le M$ $,$ $i = 1,2, $ $ \cdots $ $, n ．$ $则$

$\left(\sum_{i=1}^{n} \lambda_{i} a_{i}\right)\left(\sum_{i=1}^{n} \frac{\lambda_{i}}{a_{i}}\right) \le \frac{(M+m)^{2}}{4 M m} . $

2.波利亚（Polya）不等式

$ 设实数$ $0 \lt m_{1} \le a_{i} \le M_{1}$ $,$ $ 0 \lt m_{2} \le b_{i} \le M_{2}$ $,$ $ i=1，2, $ $\cdots$ $,n ,则 $

$\left(\sum_{i=1}^{n} a_{i}^{2}\right)\left(\sum_{i=1}^{n} b_{i}^{2}\right) \leq \frac{1}{4}\left(\sqrt{\frac{M_{1} M_{2}}{m_{1} m_{2}}}+\sqrt{\frac{m_{1} m_{2}}{M_{1} M_{2}}}\right)^{2}\left(\sum_{i=1}^{n} a_{i} b_{i}\right)^{2} .$

3.奥采尔（Aczel）不等式

$设整数$ $n \geq 2, a_{1}, a_{2}, $ $\cdots$ $, a_{n}, b_{1}, b_{2}, $ $\cdots$ $, b_{n}$ $是实数,满足$ $a_{1}^{2} \gt \sum_{i=2}^{n} a_{i}^{2}$ $,则$

$\left(a_{1}^{2}-\sum_{i=2}^{n} a_{i}^{2}\right)\left(b_{1}^{2}-\sum_{i=2}^{n} b_{i}^{2}\right) \leq\left(a_{1} b_{1}-\sum_{i=2}^{n} a_{i} b_{i}\right)^{2},$

$当且仅当$ $\frac{a_{1}}{b_{1}}=\frac{a_{2}}{b_{2}}=\cdots=\frac{a_{n}}{b_{n}}$ $时等号成立，规定$ $a_{i}=0$ $时$ $b_{i}=0$ $．$

${\color{Purple}注：以上三个不等式可称为反向柯西型不等式}$

4.伯努利（Bernoulli）不等式

$设$ $x \gt -1$ $且$ $x \ne 0$ $,$

$当$ $\alpha \gt 1$ $或$ $\alpha \lt 0$ $时,$ $(1+x)^{\alpha} \gt 1+\alpha x$ $;$

$当$ $0 \lt \alpha \lt 1$ $时$ $,$ $(1+x)^{\alpha} \lt 1+\alpha x$ $.$

${\color{Purple}广义伯努利不等式:}$

$设$  $x_{1}$ $,$ $x_{2}$ $,$ $\cdots$ $,$ $x_{n} \gt -1$ $且均非正或均非负,则$

$\prod_{i=1}^{n}\left(1+x_{i}\right) \ge 1+\sum_{i=1}^{n} x_{i}$

$当且仅当$ $x_{1}$ $,$ $x_{2}$ $,$ $\cdots$ $,$ $x_{n}$ $中至少有$ $n-1$ $个为$ $0$ $时等号成立.$

5.范数不等式

$设$ $a_{1}, a_{2}$ $,$ $\cdots$ $,$ $a_{n}$ $是非负实数,正实数$ $\alpha \lt \beta$ $.则$

$\left(\sum_{i=1}^{n} a_{i}^{\beta}\right)^{\frac{1}{\beta}} \le \left(\sum_{i=1}^{n} a_{i}^{\alpha}\right)^{\frac{1}{\alpha}}$

$当且仅当$ $a_{1}$ $,$ $a_{2}$ $,$ $\cdots$ $,$ $a_{n}$ $中至少有$ $n-1$ $个为$ $0$ $时等号成立.$

6.卡莱曼（Carleman）不等式

$\text { 设 } a_{1}, a_{2}, \cdots, a_{n} \text { 是正实数，则 }$

$\sum_{i=1}^{n} \sqrt[i]{a_{1} a_{2} \cdots a_{i}} \leq e \sum_{i=1}^{n} a_{i}$