物理 初中数学好题分享帖
[2025.12.4 已更新]![]()
![]()
![]()
![]()
![]()
$\huge{有初中数学的问题也可以发出来帖主看见了就}$
$\huge{会回答。基本上都是当天解答。}$
$\huge{记住!初中的!其余不保证。}$
看要求。- 必须是课外知识,在中学阶段较为小众。
- 前面有人发过就不要再发了。
- 评论不能开新楼。
本帖要求:
- 回答问题最好不要另开新楼(除非发出后楼上接着就是原题或其他同学的本题题解),只能在对应题目题解下评论里发,发题目时需附上题解(可以接着开一个楼,也可以在同一个回复里一起发)。若是有与题解不同的思路,可以接在题目题解下面具体说一下思路。
- 回复禁止水。

- 有什么建议可以跟帖主说,及时更新。

- 时间正序
- 时间倒序
- 评论最多
- 1
[较难]解方程组 $\begin{cases}\left|x-y\right|=x+y-2\\\left|x+y\right|=x+2\end{cases}$

(感谢@即未用户9223提醒原题解数抄错了![]() )
)
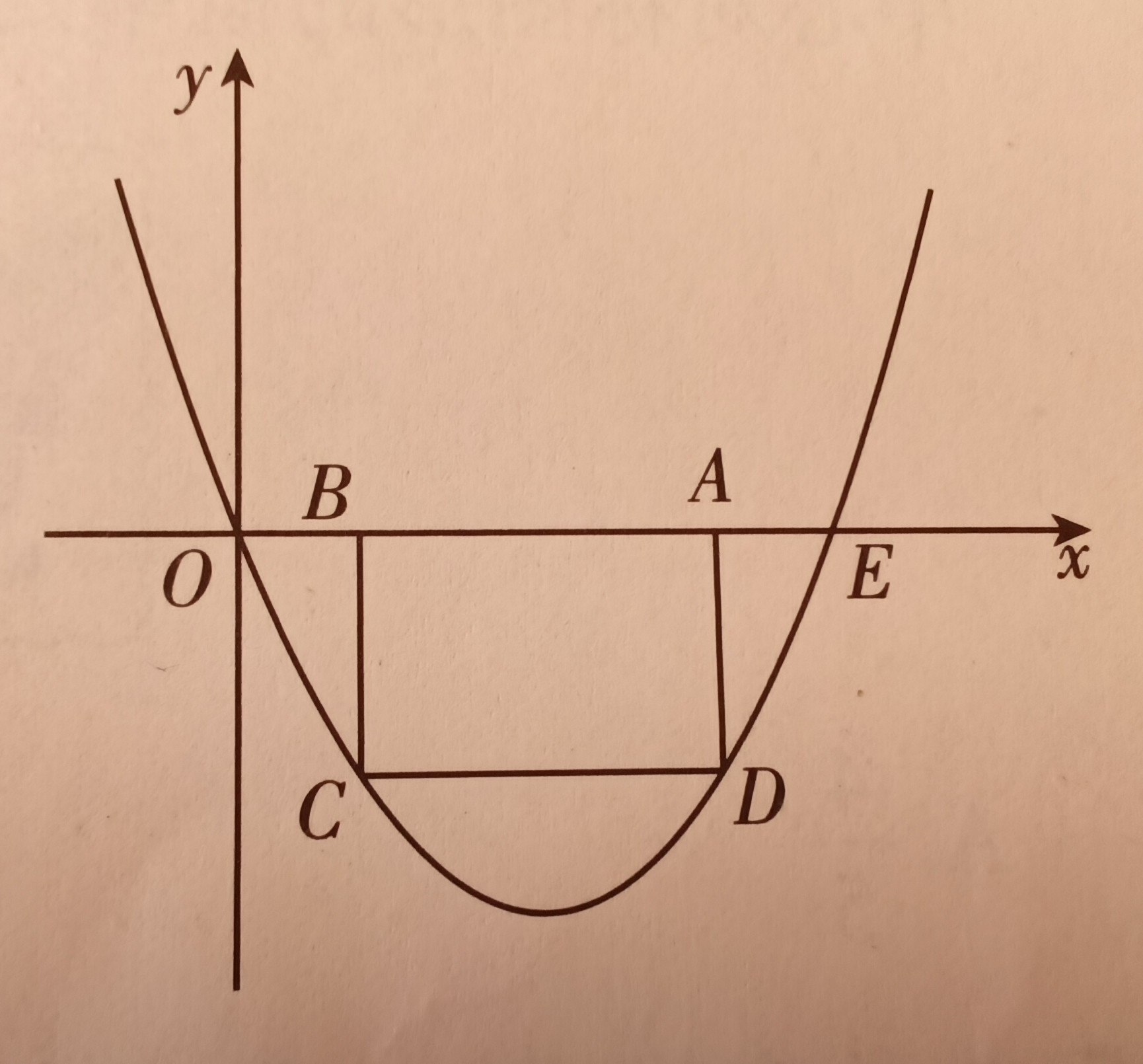
[较难]如图,抛物线过点 $O(0,0)$ , $E(10,0)$ ,矩形 $ABCD$ 的边 $AB$ 在线段 $OE$ 上(点 $B$ 在点 $A$ 的左侧),点 $C$ , $D$ 在抛物线上 . 设 $B(t,0)$ , 当 $t=2$ 时 , $BC=4$ .
(1)求抛物线的函数表达式.
(2)当 $t$ 为何值时,矩形 $ABCD$ 的周长最大?最大值是多少?
(3)保持 $t=2$ 时的矩形 $ABCD$ 不动,向右平移抛物线,当平移后的抛物线与矩形的边有两个交点 $G$ , $H$ ,且直线 $GH$ 平分矩形 $ABCD$ 的面积时,求抛物线平移的距离.
题解:

(我最后一题用的分类讨论做的,没有标答好,就不发了)
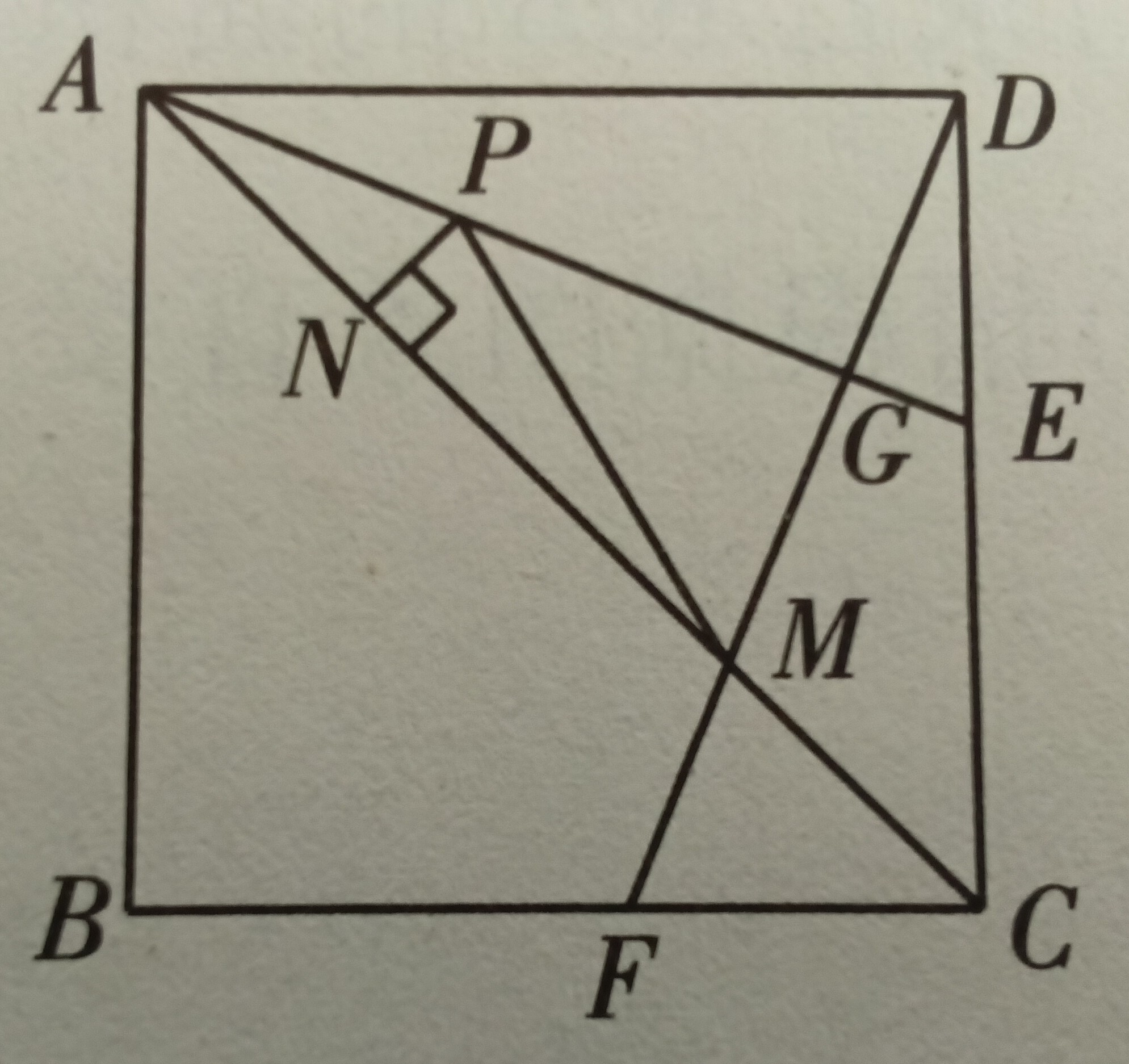
如图,正方形 $ABCD$ 的边长为 $4$ ,点 $E$ ,$F$ 分别在边 $DC$ , $BC$ 上,且 $BF=CE$ , $AE$ 平分 $\angle CAD$ ,连接 $DF$ ,分别交 $AE$ , $AC$ 于点 $G$ ,$M$ . $P$ 是线段 $AG$ 上的一个动点,过点 $P$ 做 $PN\perp AC$ ,垂足为 $N$ ,连接 $PM$ .有下列四个结论:① $AE$ 垂直平分 $DM$ ;② $PM+PN$ 的最小值为 $3\sqrt{2}$ ;③ $CF^2=GE·AE$ ;④ $S_{△ADM}=6\sqrt{2}$ .其中正确的是( )
题解:

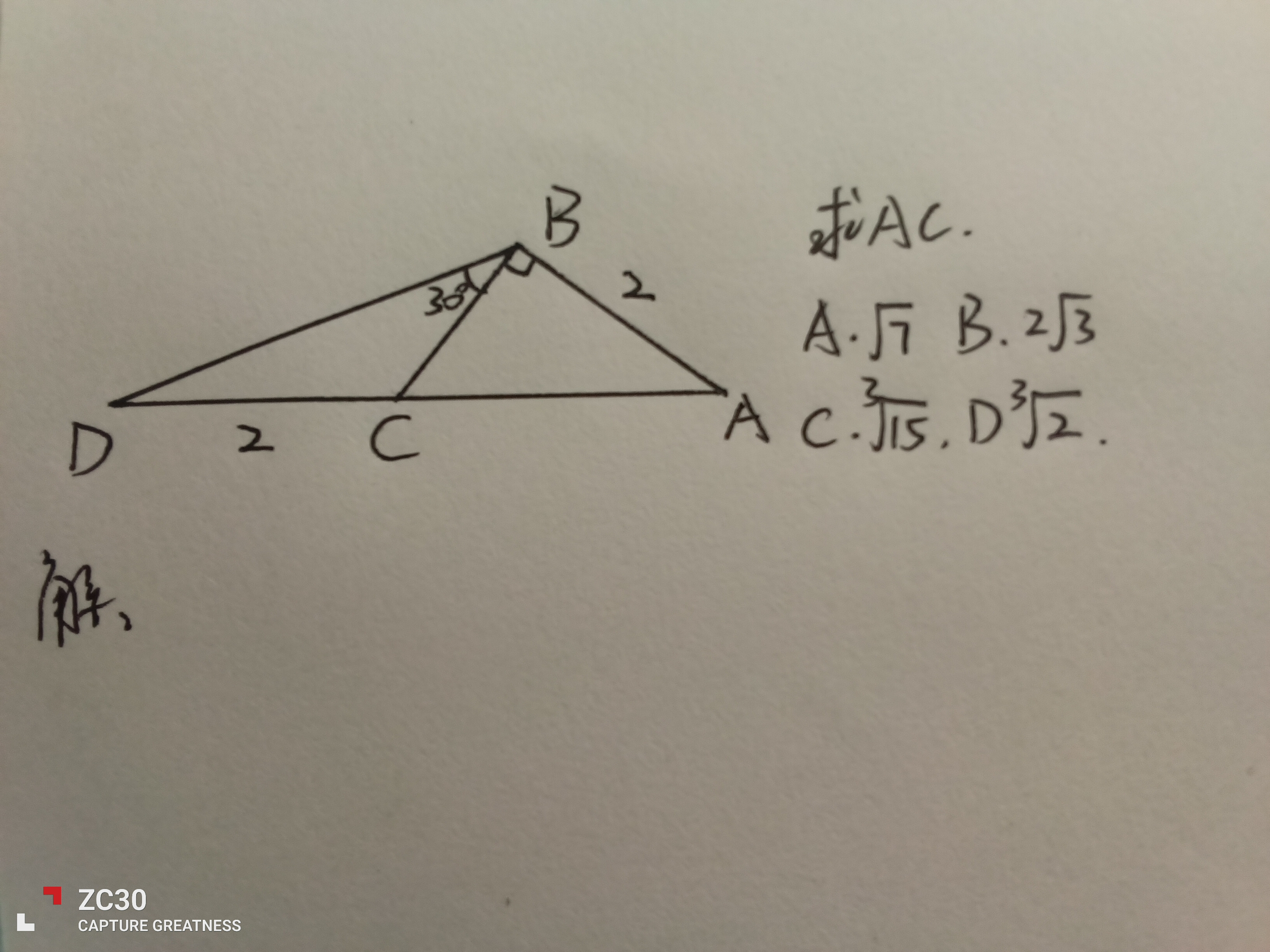
以前用一节课时间想出来用四点共圆转移30度角。 。 。
现在看余弦定理似乎也能做,但是比较难算
有没有佬能补充一下解法![]()
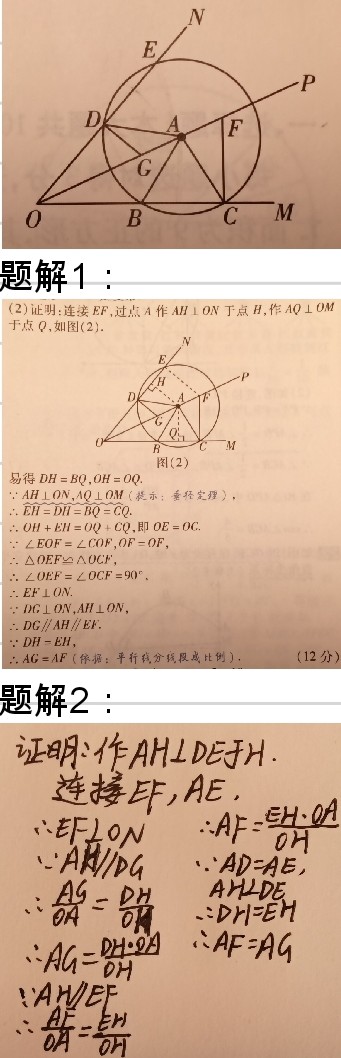
题解:

已知:射线 $OP$ 平分 $\angle MON$ ,$A$ 为 $OP$ 上一点, $\bigodot A$ 交射线 $OM$ 于点 $B$ , $C$ ,交射线 $ON$ 于点 $D$ , $E$ ,连接 $AB$ , $AC$ , $AD$ .
如图,过点 $C$ 作 $CF\perp OM$ ,交 $OP$ 点 $F$ ;过点 $D$ 作 $DG\perp ON$ ,交 $OP$ 于点 $G$ .求证: $AG=AF$ .