数学

西姆松定理及其推广？

(本人不会LaTeX，可能导致帖子可读性降低，敬请谅解♿，如有错误欢迎大家改正♿)

西姆松定理应该是二试中比较简单的定理了(有可能是因为证明过程简单)，算了还是说一下吧😅，不废话，直接开始正题♿

给定∆ABC和它的外接圆O，点P为平面内一点，过P分别作PD垂直AB，PE垂直AC，PF垂直BC，垂足分别为D，E，F

则P在圆O上的充要条件是D，E，F三点共线(这条线即为西姆松线)

它的必要性可以证明三点共线，充分性可以用来证明四点共圆

其实它的证明过程非常之简单，用三个四点共圆倒角就行♿♿(所以PD，PE，PF也不一定要垂直三边，只要满足这三个四点共圆就行了？)

而且一般情况下它的意义不是很大♿♿♿(而且证三点共线和四点共圆的方法太多了，这个应该算是比较冷门的一个了？) (可能在二试中连作为引理都不够格😅♿，这也可能是二试很少涉及它的原因之一了)

不过，今天我在做题时发现了这样一个问题：

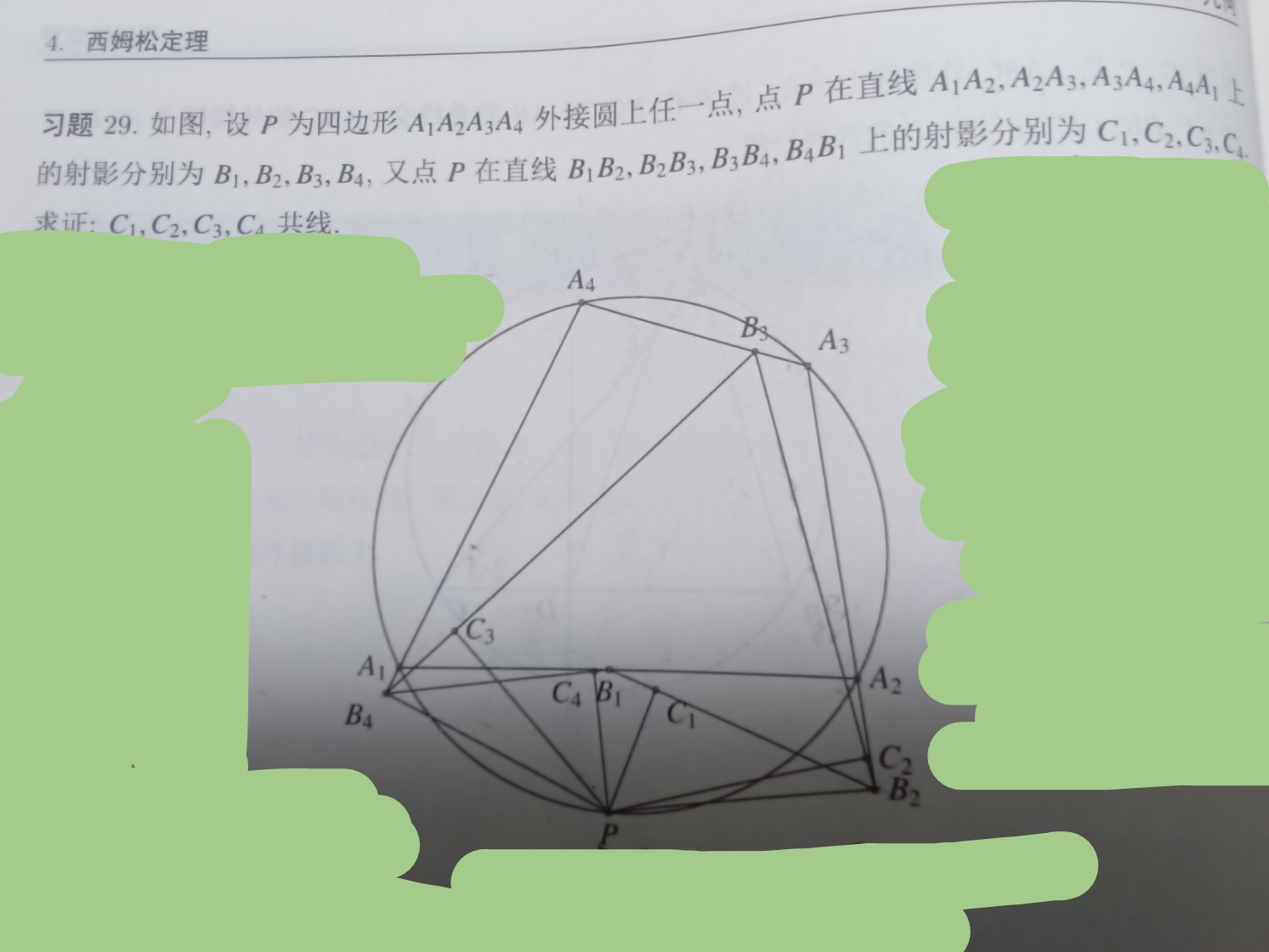
这个问题看上去和西姆松很像(四边形的西姆松，不过要有两组垂直)，但是要想证明它却要用三角形的西姆松导出一堆三点共线外加一个四点共圆♿

(可以xue微想一下这个问题？解答放在评论区♿)

这让我突然想到，(圆内接)三角形要用一组垂直得到共线，圆内接四边形要用两组垂直得到共线，那么圆内接五边形是不是要用三组垂直？

于是我突发奇想，画了圆内接五边形的图↓(由于把所有垂线都画出来的图可能很乱，所以我只画了垂足，可能一些点会看上去重合了，凑合着看吧😂)(画红色圆圈的的是第3组垂足)

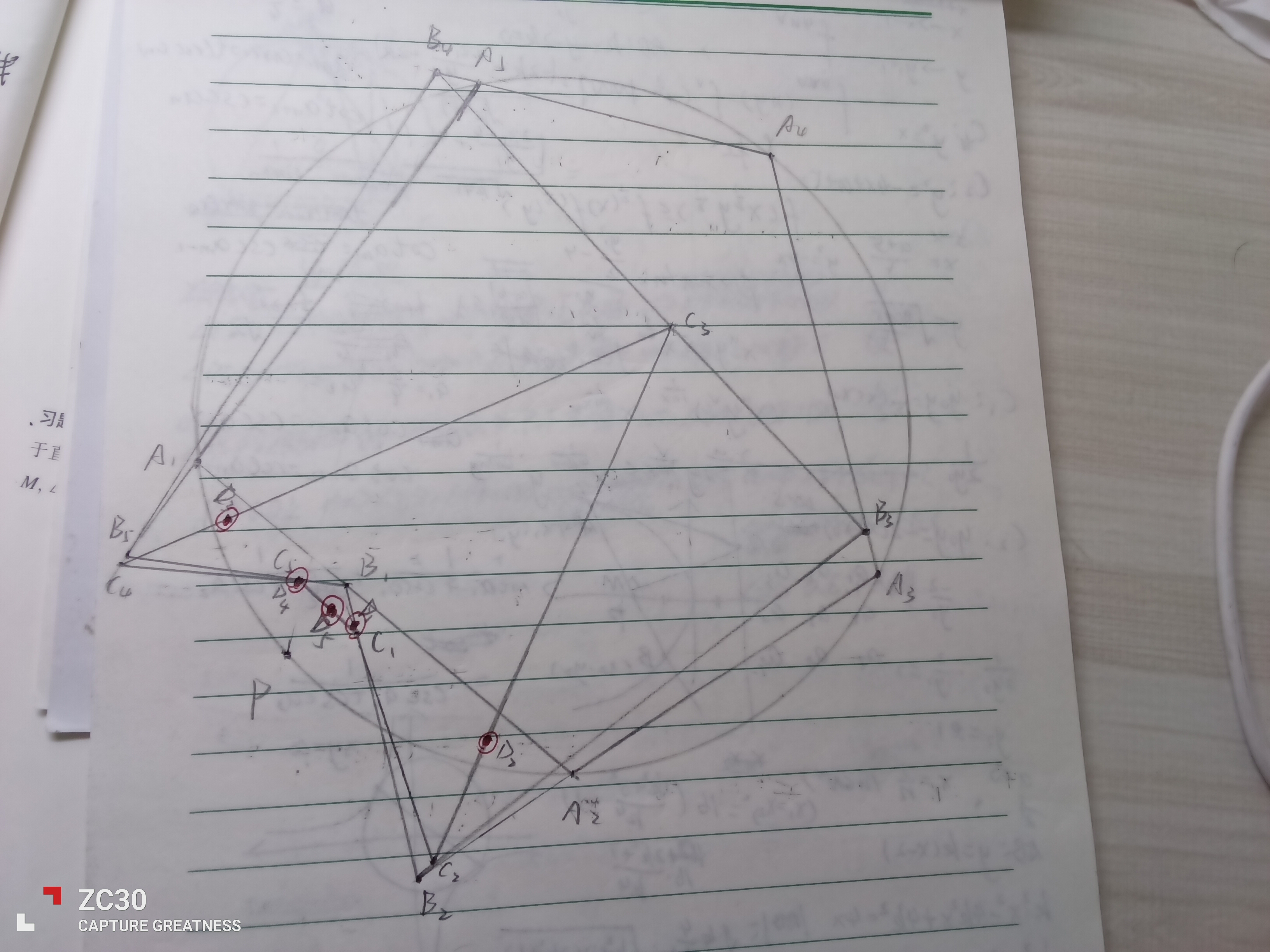
真是非常的Amazing啊(毕导音)，它们竟然也是共线的？(我暂时还没证出来😅，不过应该和圆内接四边形的情况差不多)

所以我大胆猜测，对于圆内接正n边形，也有类似的结果：

有没有哪位佬证明一下？😅

如果有人给出证明，我会考虑出下一期♿(最近有点忙，还要准备高联♿，可能不会更，敬请谅解♿♿)