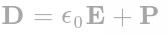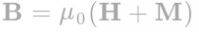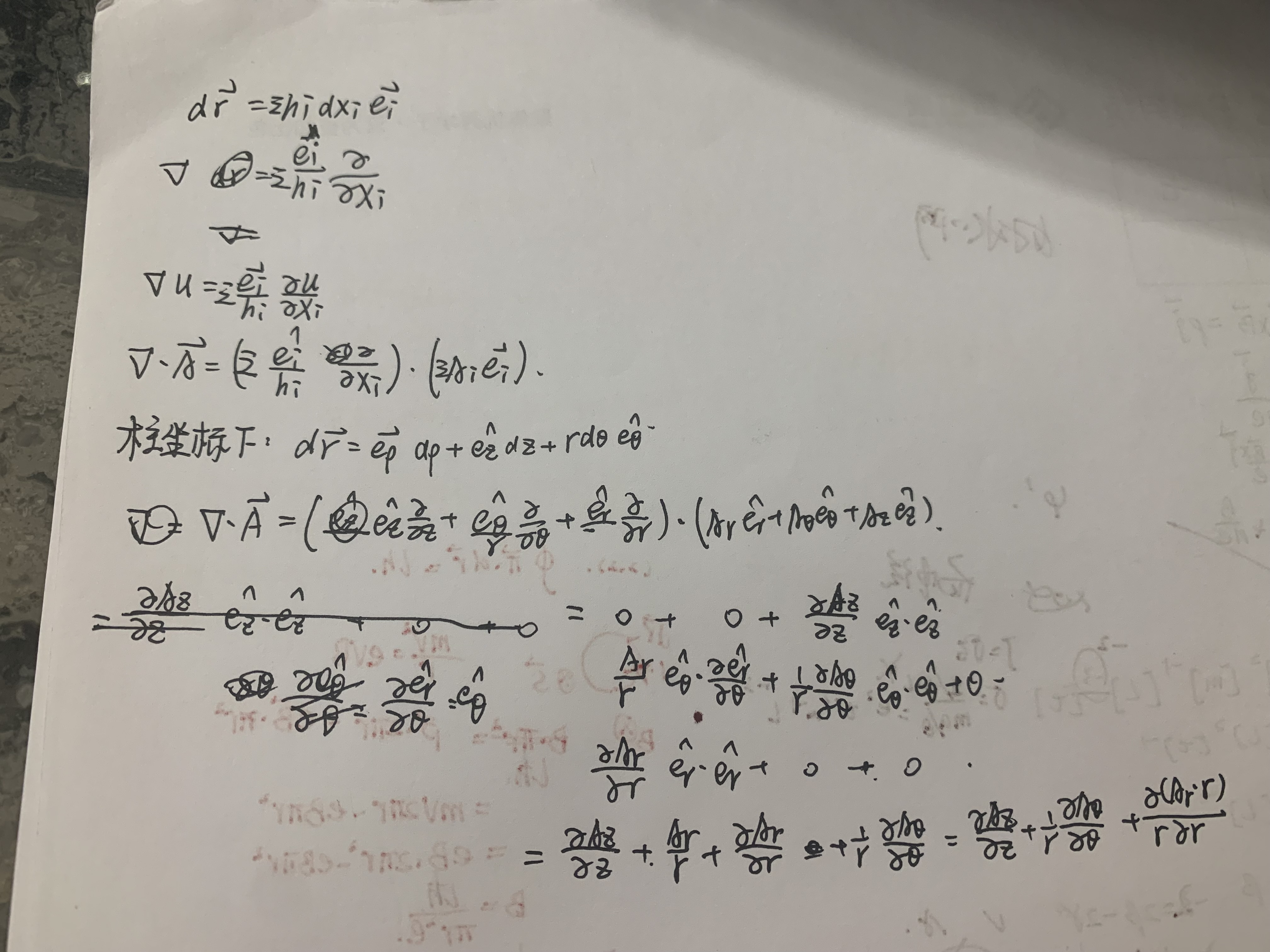物理

物理学中的数学工具

因为目前我的时间比较紧迫，来不及写过多的前言，所以我就简短的说几句，等日后有时间了再来补档这个无所谓有，又无所谓无的前言

这个帖子出现于此仅有两个原因：

1，深化我自己的理解

2，方便有需要的同学们进行查询和使用，增加o－box的学术性（就目前而言o－box里没有价值的帖子太多了）

注意，阅读本帖至少需要一定的微积分和导数基础，最好还有一定的物理基础方便理解。

由于这是我第一次尝试使用规范的书写进行编写，可能存在很多疏漏，欢迎各位来帮助我

若本帖出现学术性错误，欢迎指正

一，梯度，散度，旋度与Maxwell 方程组

（1）首先我们应该明白，nabla算符本身是一个矢量，因此当他作用在不同的量上的时候会出现不同的效果

1，梯度是nabla 算符点乘一个标量的结果，矢量点乘标量是一个矢量，因此对一个标量求梯度结果是矢量

举例：对电场是电势的负梯度

2，散度是nabla 算符点乘一个矢量的结果，对一个矢量求散度结果是一个标量

举例：对于一个有源或者有汇的电场，我们对其求散度等价于高斯定理

3，梯度是nabla 算符叉乘一个矢量的结果，对一个矢量求旋度结果是一个矢量

举例：对于一个有旋度的磁场，我们对其求旋度等价于安培环路定理

实际上，高斯定理和电场散度，以及安培环路定理与磁场旋度的区别是前者为积分形式而后者为微分形式

（2）接下来讲讲怎么求解梯度，散度和旋度

 1. 拉梅系数

为了更方便地给出梯度，散度和旋度在各个坐标系下的形式，我们引入拉梅系数

 2. 梯度

3. 散度

 4. 旋度

但是，我并不喜欢这个写法，因为旋度写成行列式的形式更加简洁好看：

下面给出最常用的坐标系（柱坐标和球坐标）下的梯度，散度和旋度公式，方便忘记了的同学们进行查阅：

1）柱坐标系（Cylindrical Coordinate System）

梯度：

散度：

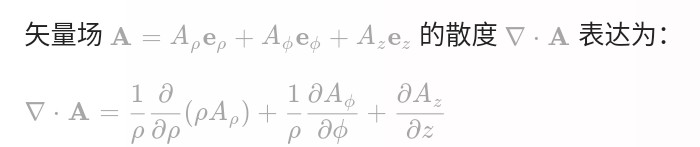
旋度：

2）球坐标系（Spherical Coordinate System）

梯度：

散度：

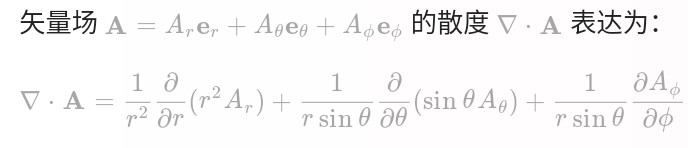
旋度：

以下有两点值得注意：

1，针对刚刚掌握求导的同学：以上式子中，偏导数后面跟着的括号内的两个相乘的量在展开时，满足乘法求导的规则，即你的导数乘我＋我的导数乘你，切忌无视规则直接打开括号；

2，对于梯度和散度，在二维，三维或是四维乃至更高维都可以有所定义，但是旋度仅在三维中有所定义，这是因为叉乘就是定义在三维里的向量乘法规则，对于更高维度需要重新定义

好了，现在大家差不多掌握了梯度，旋度和散度的性质及其运算规则，接下来可以来深入讲讲如何理解这几个运算符号了

为了深入理解，我们结合物理里面的应用，也就是大名鼎鼎的麦克斯韦（Maxwell）方程组

这几个方程涵盖了所有静电静磁学的内容，按理来说所有静电静磁学的问题只要列出了这几个方程就都可以解决（但也只是理论层面，毕竟很多情况我们都需要化简这些所谓的方程）

（2）Maxwell 方程组

其实Maxwell 方程组远没有大家想象的那么简洁，下面先给出他的完整形式供大家参考：

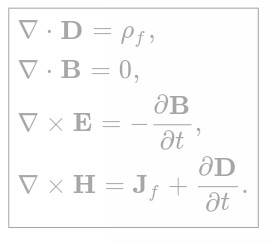
是不是和大家想象的有所差距呢？

在上述方程中，电位移矢量D和磁场强度H相对应，电场强度E和磁感应强度B相对应，至于这些量之间的详细推导我们这里不做过多的讲解，只是给出他们之间的转化关系：