物理

《物理竞赛专题精编》 江四喜编著（注：此帖仅为搬运贴）

$\huge{最近刚开一轮带着啃，有些题目对新手还算友}$

$\huge{好，同时书本身比较贵，所以免费帮大家搬运！}$

但是坚果猫才疏学浅啊，不知道能不能担的上这本书的重量，所以先更着看吧，大家有什么建议或者错误的指正都可以在下面评论或者回复，实在卡CD也可以＠我哟@一水合坚果猫（一轮焕新版）

先放全部区吧，更的多了再改O-box～

$\huge{1. 相对运动}$

        相对运动不仅是研究运动学乃至整个物理学的基础，也是研究矢量问题的出发点.通过对不同的位移、速度、加速度之间的转换与运算，我们可以对矢量的运算及复杂的运动有一个基本的认识.

        在竞赛中，求解相对运动的问题单独成题的可能性并不太大，但能否较好地处理相对运动的问题，又往往是能否正确解答相关问题的关键所在.同时，在很多情况下，运用好相对运动间的关系，能很大程度上减少运算量，简化解题步骤，提高解题速度.能否熟练地处理这类问题也在一定程度上反映了答题者思维的敏捷程度.

1. 两辆汽车的挡风玻璃与水平方向的夹角分别为 $\beta_1 = 30^\circ$,$ \beta_2 = 15^\circ$.冰雹竖直下落，打到玻璃上，两司机都看到冰雹从玻璃上反弹后竖直向上运动，求两车速率之比.

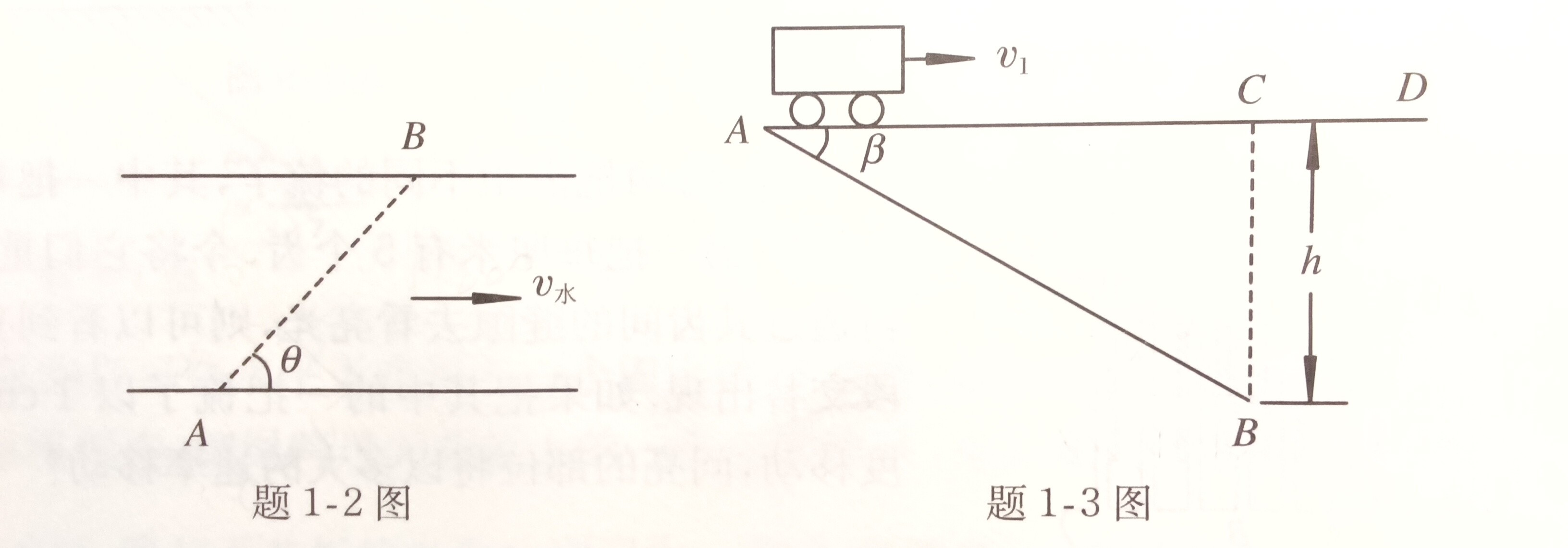
2. 在河流两岸相距$s =1200m$ 处有 A、B 两码头，A、B 两码头和河岸成 $\theta = 60^\circ$ 角，且 B 在 A 的下游，如图所示。水流速度 $v_{水}=1.9m/s$.一艘渡船想在最短时间 $t = 5min$ 内沿直线 AB 往返于两码头间，问船应取怎样的方向航行？船速多大？

3. 一人站在距平直公路 $h = 500m$的 B 处，公路上有一汽车以$v_1=10m/s$的速度行驶，如图所示.当汽车在与人相距 $l = 200m$的 A 处时，人以速度 $v_2=3m/s$奔跑（可以认为人开始就是这个速度）.为了使人跑到公路上时能与车相遇，问：

   (1) 人奔跑应取什么方向？

   (2) 人需要多长时间才能赶上汽车？

   (3) 若其他条件不变，人在原处开始匀速奔跑时，该人可以与汽车相遇的最小奔跑速率是多少？

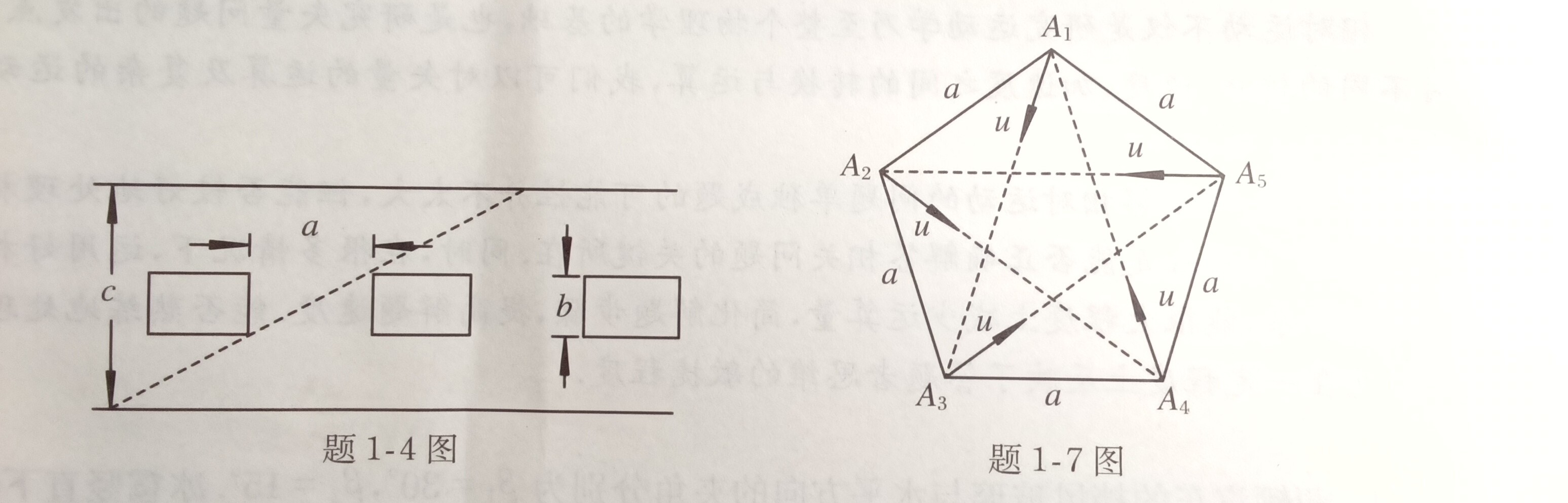
4. 如图所示，一相同的汽车以等速$v$沿宽度为$c$的直公路行驶，每车宽为$b$，头尾间距为$a$，则人能以最小速率沿一直线穿过马路所用时间为多少？

5. 模型飞机以相对于空气 $v=39km/h$的速度绕一个边长为$2km$的等边三角形飞行，设风速$u=21km/h$，方向与三角形的一边平行并和飞机起飞方向相同，问飞机绕三角形一周需要多少时间？（忽略飞机转弯与起飞所需的时间.）

6. 一木板从空中下落，发现在某时刻板上 $a$ 点速度和$b$点速度相同，$v_a=v_b=v$，且均位于板面上；同时还板上$c$距离等于$a$、$b$两点之间距离，则板上哪些点的速度等于$3v$？

7. 各边长为$a$ 的正五边形的五个顶点上各有一个质点，分别为$A_1$、$A_2$、$A_3$、$A_4$和$A_5$，如图所示.今使质点$A_1$始终对准质点$A_3$运动，$A_3$始终对准$A_5$运动，$A_5$始终对准$A_2$运动，$A_2$始终对准$A_4$运动，$A_4$始终对准$A_1$运动，运动速率均为$u$.试问经多长时间五个质点相聚？

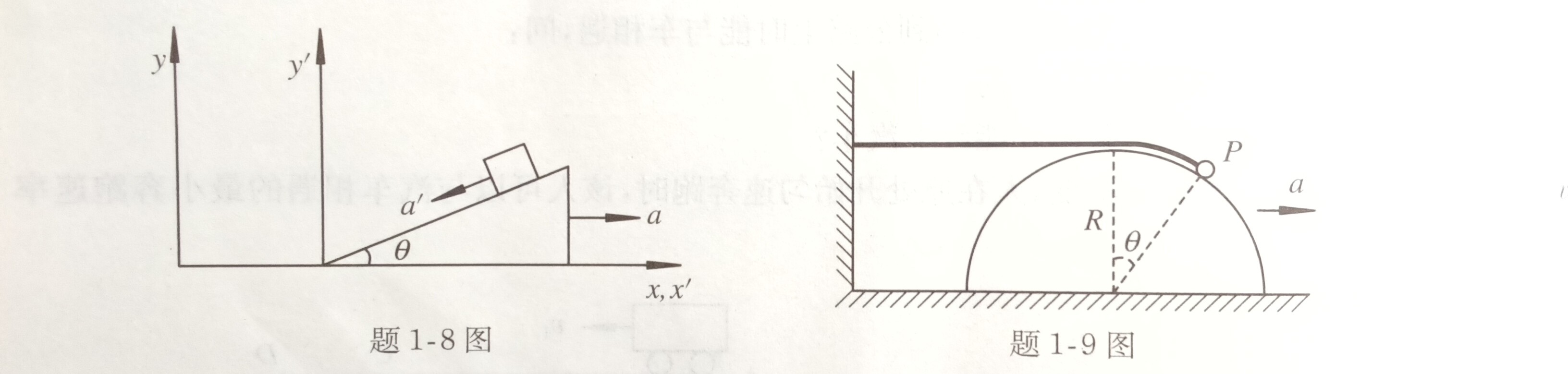
8. 如图所示，一斜面体放置在光滑的水平面上，一木块沿斜面以相对加速度（相对斜面体）a'下滑，斜面体获得向右的加速度$a$.试求木块相对地面的加速度$a_0$.（已知斜面倾角为$\theta$.）

9. 一半径为$R$的半圆柱面在水平面上向右做加速度为$a$的匀加速运动，在柱面上有一系在水平绳子自由端的小球$P$，绳子的另一端固定在墙面上.如图所示，当小球相对于半圆柱面的角位置为$\theta$时，半圆柱面的速度为$v$，求此时小球的速率和加速度的大小.

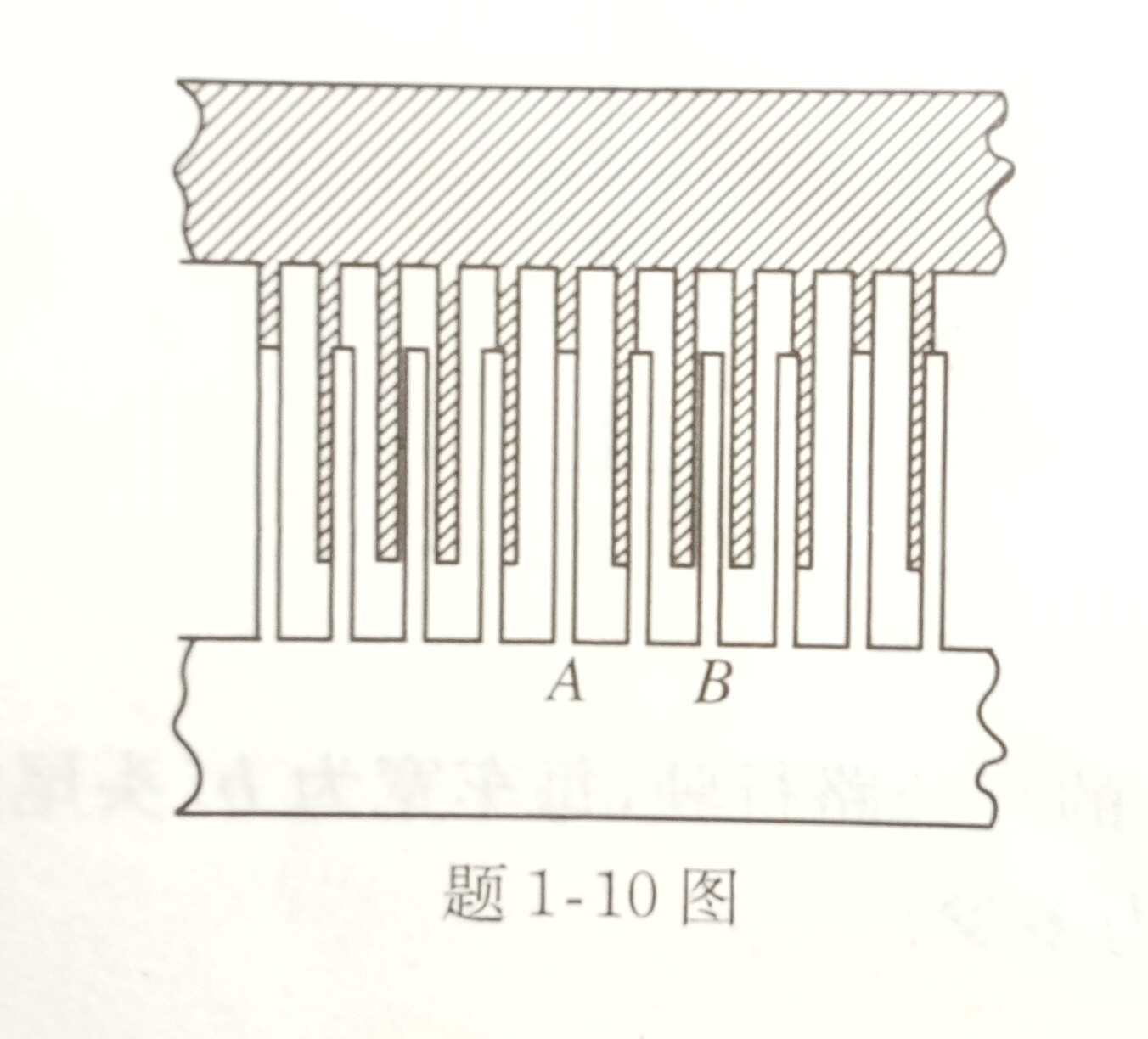
10. 有两把齿距不同的梳子，其中一把每厘米有 4 个齿，另一把每厘米有 5 个齿.今将它们重叠起来，再透过其齿间的缝隙去看亮光，则可以看到亮段和暗段交替出现.如果把其中的一把梳子以$1cm/s$的速度移动，问亮的部位将以多大的速率移动？

$\huge{ 2.速度与加速度关联}$

       通过绳或杆连接起来的物体的速度、加速度之间的关系既是运动的合成与分解的运用能力的体现，也是小量运算的基础。

       对物体间的速度与加速度的关联，应注意以下几方面：一是通过绳连接起来的物体，在绳没有跨过动滑轮的前提下，绳上各点沿绳的方向上的速度大小相等，但加速度未必相等；二是相互接触的坚硬物体，在垂直于接触面的方向上各物体的速度相等；三是在没有转动和动滑轮的前提下，在沿绳的方向上，各点的加速度相等（杆亦有类似的性质）。

       一般情况下，速度与加速度的关联并不单独成为赛题，而是渗透在其他问题之中，但能否迅速而准确地找到物体间的这种关联，往往是能否正确解题的前提与基础。

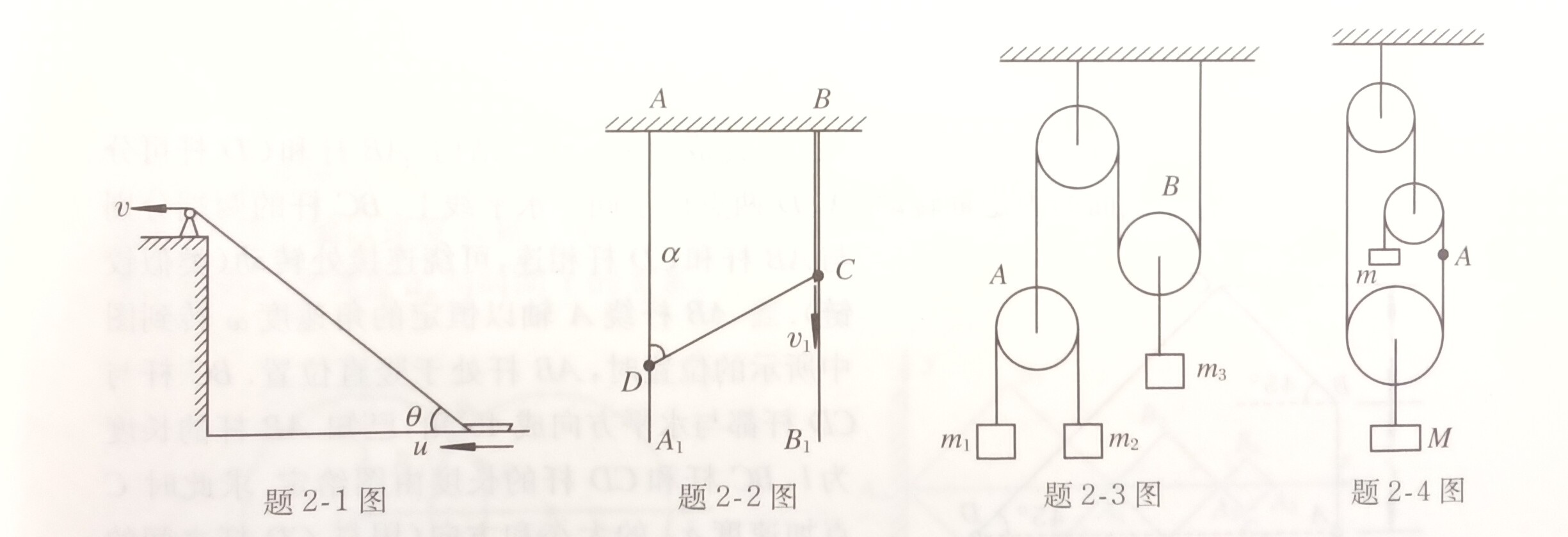
1. 如图所示，人在河岸上用绳经滑轮拉船靠岸。若当绳与河面夹角为 $\theta$  时，绳的速率为 $v$ ，试求此时船靠岸的速率$u$及加速度$a$。 

2. 如图所示，$AA_1$和$BB_1$是两根光滑的细直杆，并固定在天花板上，将绳的一端拴在$B$点，另一端拴在套于$AA_1$杆上的珠子$D$上，另有一珠子$C$穿过绳及杆$BB_1$以速率$v_1$匀速下落，而珠子$D$以一定速度沿杆上升。当图中角度为$\alpha$ 时，珠子$D$上升的速率$v_2$多大？

3. 在如图所示的装置中，已知三物体的质量分别为$m_1$、$m_2$和$m_3$，其中质量为$m_3$的物体向上做加速运动。若忽略滑轮和绳的质量及一切摩擦，求质量为$m_3$物体的加速度。

4. 在如图所示的系统中，滑轮与线的质量轻，可忽略不计，线不可伸长，滑轮的大小正好使图中的线是竖直的。问图中两物块$M$和$m$的加速度分别为多少？线上有一点$A$，如图所示，该点的加速度为多少？

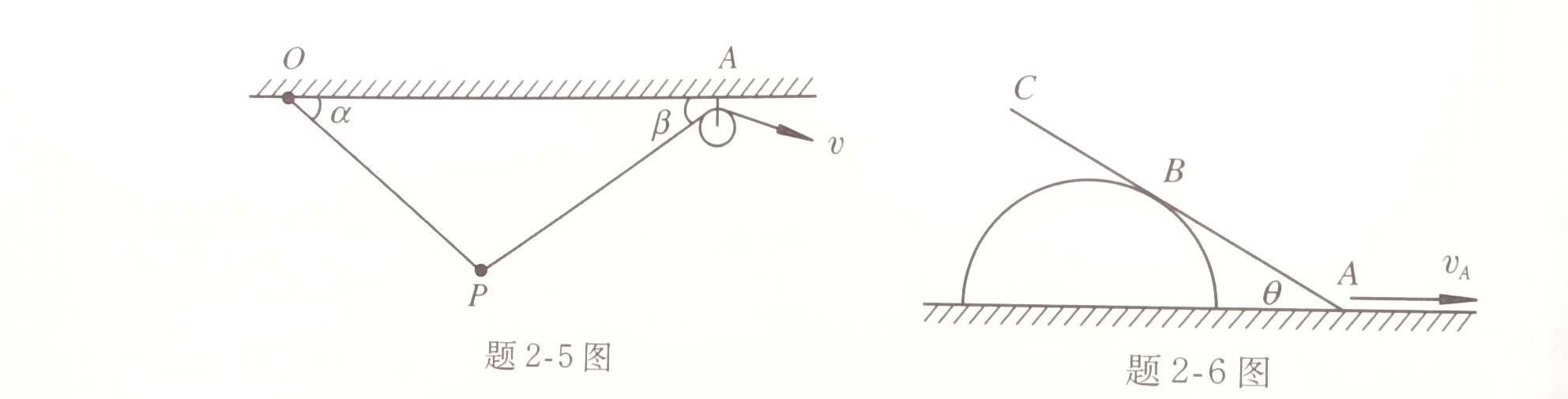
5. 某细杆可绕水平天花板上一个固定轴$O$旋转，细杆的另一端连接小球$P$，小球$P$ 又与一根细绳相连，细绳跨过天花板上的一个小滑轮$A$，可以被人用手拉动。已知$OA$间的距离为$L$，细杆、绳与天花板的夹角分别记为$\alpha$和$\beta$，如图所示。设某时刻$\alpha+\beta\le\frac{\pi}{2}$，绳被拉动的速率为$v$，试求此时小球$P$的运动速率$u$及加速度$a$。

6. 如图所示，细杆$ABC$靠在固定的半圆环上，两者处于同一竖直平面内，杆上$B$恰好落在圆环上，圆环的半径为$R$。已知$A$端沿半圆直径方向移动的速率大小为$v_A$，求当杆与水平线的交角为$\theta$时：

   (1) 杆的角速度$\omega$;

   (2) 杆上与半圆相切点$B$的速率和杆与圆环接触点$B'$的速率大小。

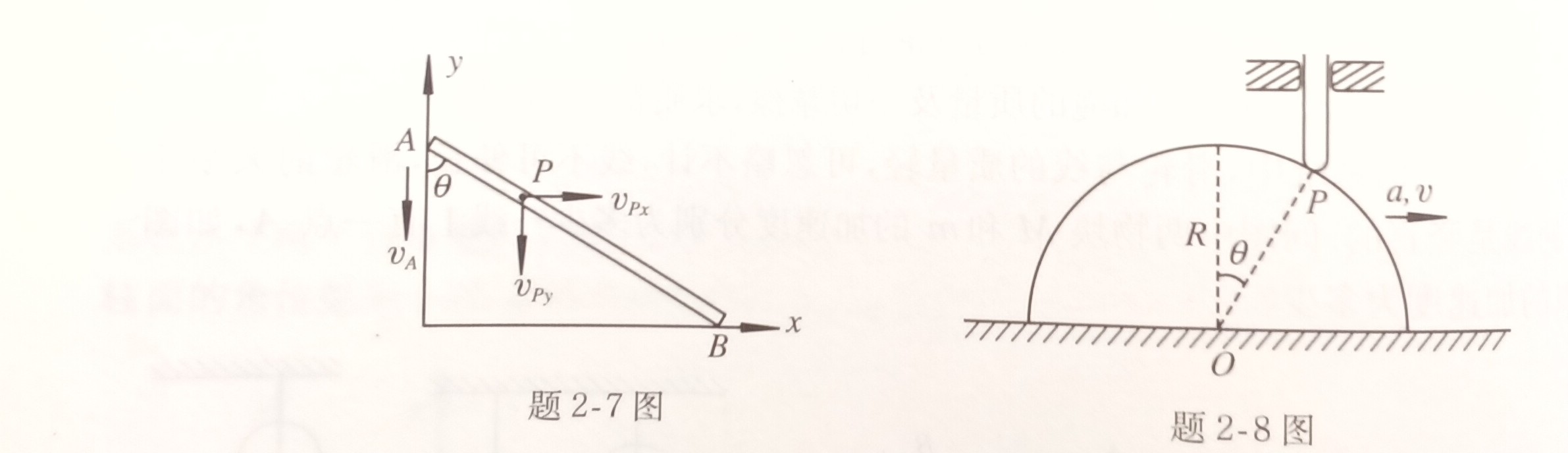
7. 如图所示，细杆$AB$长$L$，端点$A$、$B$分别被约束在$x$和$y$轴上运动，试求：

   (1) 杆上与$A$相距$\alpha L$ ($0 < \alpha < 1$）的$P$点的运动轨迹；

   (2) 如果已知图中$\theta$角和$v_A$，那么$P$点在$x$、$y$方向上的分运动速率$v_{Px}$、$v_{Py}$是多少？

8. 一个半径为$R$的半圆柱体沿水平方向向右做加速度为$a$的在半圆柱体上放置一根竖直杆，此杆只能沿竖直方向运动，如图所示。当半圆柱体的速度为$v$时，杆与半圆柱体的接触点$P$和柱心的连线与竖直方向的夹角为$\theta$，求此时竖直杆运动的速率和加速度。

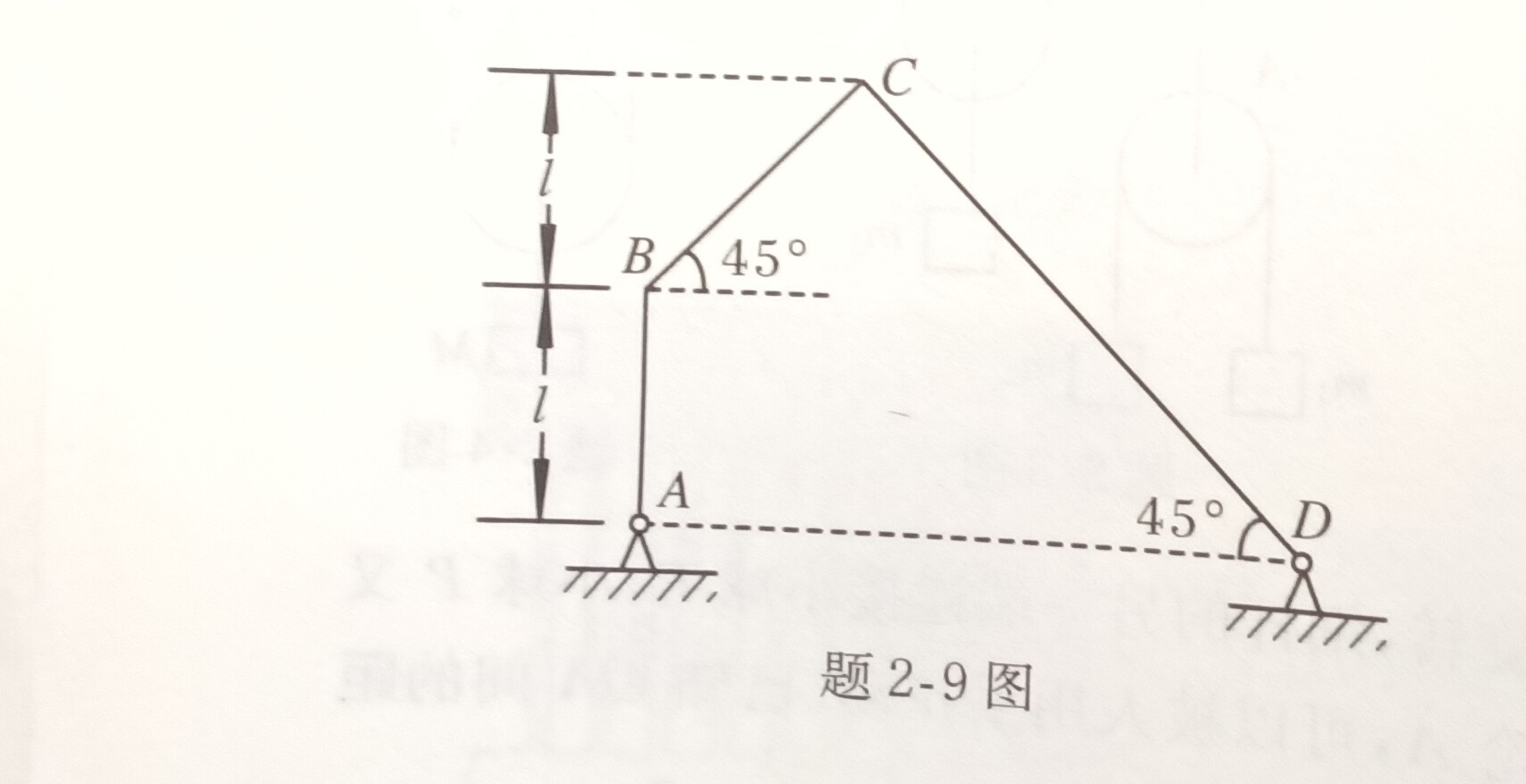
9. 图示的为用三角形刚性细杆$AB$、$BC$、$CD$连成的平面连杆结构。$AB$杆和$CD$杆可分别绕过$A$、$D$的垂直于纸面的固定轴转动，$A$、$D$两点位于同一水平线上。$BC$杆的两端分别与$AB$杆和$CD$杆相连，可绕连接处转动（类似铰链）。当$AB$杆绕$A$轴以恒定的角速度$\omega$转到图中所示的位置时，$AB$杆处于竖直位置。$BC$杆与$CD$杆都与水平方向成 $45^\circ$角，已知$AB$杆的长度为$l$，$BC$杆和$CD$杆的长度由图给定。求此时$C$点加速度$a_C$的大小和方向（用与$CD$杆之间的夹角表示）。