物理 2025东南赛试题(本人回忆版)
由于比赛结束，各大公众号已经发布试题，我今天就不打第二天的题了
此帖就作问题讨论贴吧(拒水)
呜呜呜，贴主考了33分但是贴主没有完整的做出一道题🤣
$\huge{高一}$
$\large{第一天}$
$一、正整数数列\{a_m\}，m≥6为偶数，a_1=1，满足：$
$1，a_{i+1}-a_i∈\{a_k|1≤k≤i\}$
$2，a_2,a_4,…,a_m为等差数列$
$(1)若有一项为2025，求最小的m$
$(2)若数列有22项，满足条件的数列有多少种$
$二、求所有的素数p，满足：$
$∃互不相同的a,b,c∈\{0,1,2,…,p-1\}，s.t.a^b \equiv b^c \equiv c^a \pmod{p}$
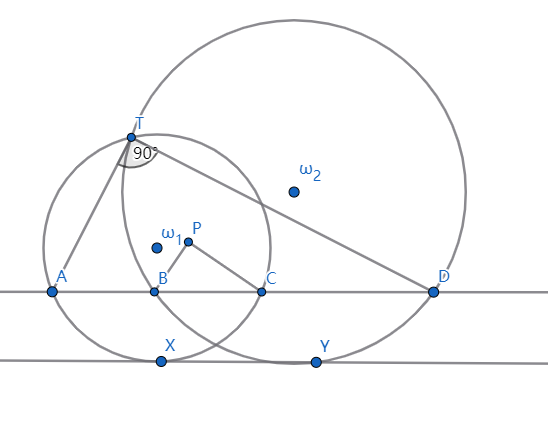
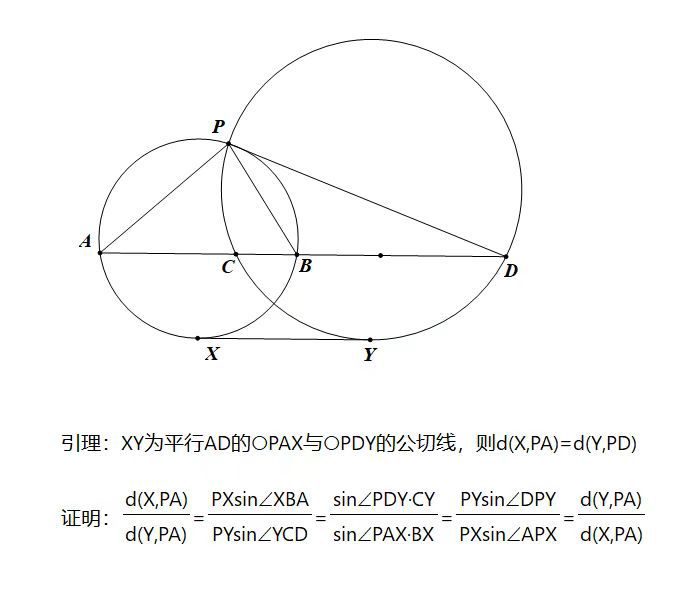
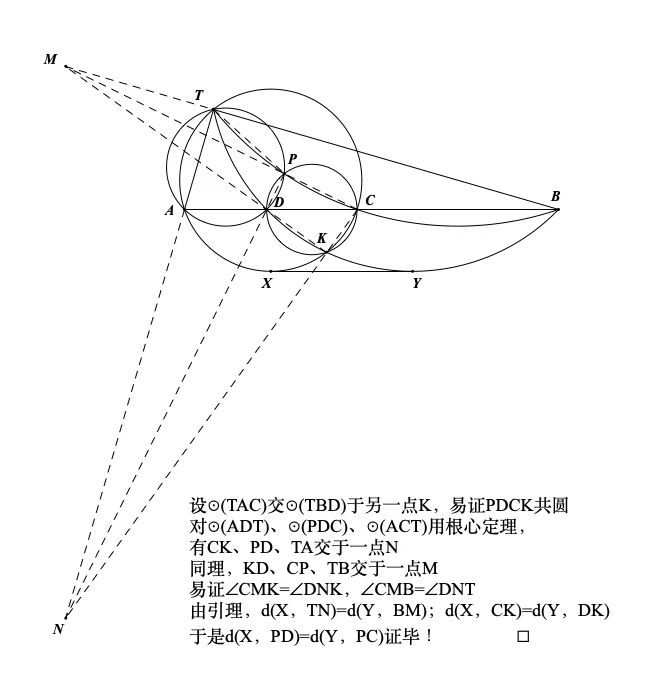
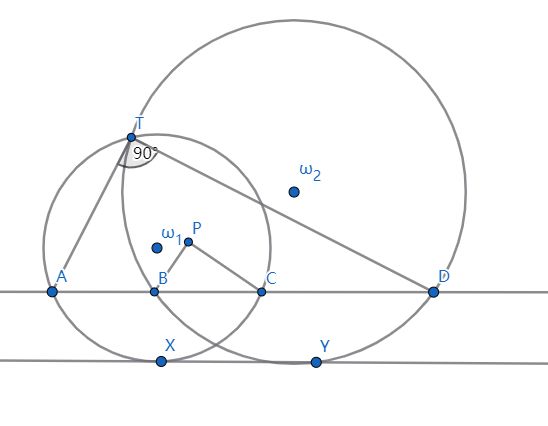
$三、如图：$
两圆ω_1,ω_2相交，记为T，两圆的公切线切与X,Y$
$做XY的平行线个两圆顺次记为A,B,C,D$
$过A,T,B和C,D,T的两圆交于异于T的P$
$设∠ATD=90°,求证：X到PB的距离等于Y到PC的距离$
$四、定义“整点”为空间直角坐标系内三个分向量都为整数的点$
$求证：∃常数c，对∀n∈N_+和任意凸多面体$
$满足：若该多面体内的的“整点”不能被n个平面完全覆盖，则也不能被cn^2条直线覆盖$
$四、定义“整点”为空间直角坐标系内三个分向量都为整数的点$
$求证：∃常数c，对∀n∈N_+和任意凸多面体$
$满足：若该多面体内的的“整点”不能被n个平面完全覆盖，则也不能被cn^2条直线覆盖$
- 1
@Fertilization
@爱数物的5汉再看一下，我刚刚少打了个90度的条件
okok
我用des帮你画画
抱歉，今天刚看到。
昨天在迷上看到两个方法，你可以去看看，都不用繁严，都很优雅。
不一样
你们下午听的什么讲座
我不带去听了，都是一些大学招生讲座，没什么干货
(今天下午讲题我去听了听，太粗略了，那么多难题一笔都没话，听的我云里雾里)
除了48每道做了半道😭
第一题我tm没睡醒少讨论个条件
第二题abc排了0和1之后排了p=3,5之后一直在想升幂定理，没往构造上想，坚定自己觉得无解
痛失两水题
三题没那么简单，我们今天下午讲的一种几何一种三角没用圆幂
第二天的A5我用因式分解大概放了下求导做的，但今天下午讲的直接注意到一个非常抽象的恒等式，然后简单放缩就证明了
G6要证共圆和找圆心共圆1分钟拿下但是圆心证了我1个小时，最后小伪了一下，听人家讲的时候才发现不简单，需要布洛卡定理，只能拿下9分低保
C7构造正确，但是我计算奇数情况的时候等差数列求和算错了😭😭😭，我甚至没觉得奇数和偶数差别那么大会有问题，哭晕了
C4需要一些高等的东西，初等方法非常复杂就没讲，这道题就没听懂
N8是一道多项式的数论整除问题，要证可以因式分解，第一步要求出多项式的根，至少我想到要求根，但就是没求出来😂
总体看不是很难，但就算没完整做出来，都是差一点(哈哈，差一点切5道，想都不敢想)
东南赛有铜牌保底吗
怎么可能，如果不是0有优胜奖
我勒个G4G8写不出，其他全浪掉哇，这是真的有点可惜了
前两题人机，但第一题刚烈了，只拿了3分，第三题考场硬模3个小时，狂砍0分，第二天前三题也是人机，但第二题证完共圆，和两个比较复杂的半径后，直接忘证两条人机半径了(我以为已经证了
)，痛失六分
