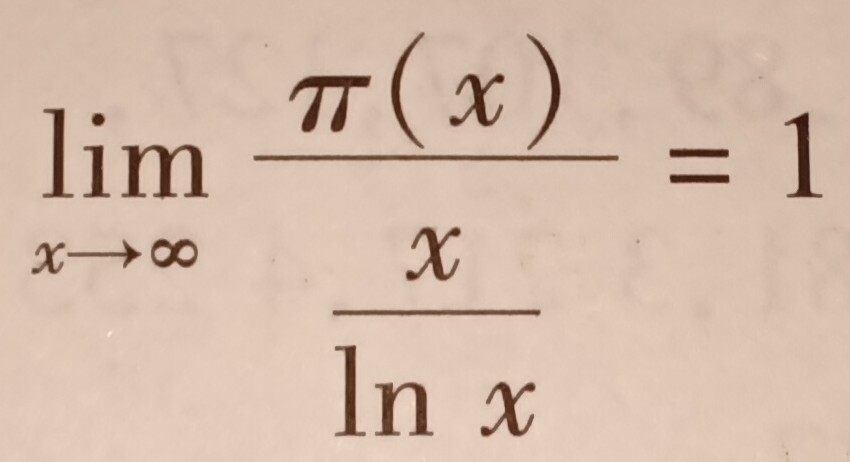初等数论～ - 质心论坛

所有/|均代表不整除 , 所有°均代表循环节 , 知道后会改的 , 见谅🙏。

有空更，可能删帖

$\color{cyan}{素数和复合数}$

定义2 一个大于1的正整数 , 只能被1和它本身整除 , 不能被其他正整数整除 , 这样的正整数叫作素数（也叫质数) , 常用p表示.

定义3 一个正整数除了能被1和本身整除以外 , 还能被另外的正整数整除 , 这样的正整数叫做（复）合数.

定义4 若a为正整数且b | a , 而b为素数 , 则b为a的素（或质）因数.

引理5 若a为整数且a>1 , 则a的大于1的最小因数一定是素数.

引理6 若a为整数且a>1 , 而所有≤√a的素数都除不尽a , 则a是素数.

引理7 素数无穷.

$\color{cyan}{素数分布的简单概况}$

我们常用π(x)表示不大于x的素数个数 , π(3)=2 , π(100)=25 , π(1000)=168.

当x越大 , π(x)与$\frac{x}{ln~x}$比值近似1.

当x越大 , π(x)与x比值近似0.

歌德巴赫猜想：凡大于4的偶数都是两个奇素数之和.

梅森数：$\Huge{M_p~=~2^p-1}$ 其中p为素数.

费马数：$\Huge{F_n~=~2^{2^n}+1}$ 其中n≥0.

$\color{cyan}{最大公因数和最小公倍数}$

定义5 若$a_1$ , $a_2$ , $a_3$ ,..., $a_n$为正整数(n≥2)且存在一正整数d , 使得d|$a_1$ , d|$a_2$ ... d|$a_n$ , 则d为$a_1$ , $a_2$ , $a_3$ ,..., $a_n$的公因数.公因数中最大的那个数为最大公因数 , 最大公因数为其他所有公因数的倍数.若d为最大公因数 , 则($a_1$ , $a_2$ , $a_3$ ,..., $a_n$)=d.

引理8 若a , b都是正整数 , 且a>b , 满足a=bq+r , 0<r<b , 其中q和r都是正整数 , 则(a,b)=(b,r).

定义6 若整数n≥2 , 而$a_1$ , $a_2$ , $a_3$ ,..., $a_n$为正整数 , 当($a_1$ , $a_2$ , $a_3$ ,..., $a_n$为正整数) = 1时 , 我们就说$a_1$ , $a_2$ , $a_3$ ,..., $a_n$互素.

定义7 若整数n≥2 , 而$a_1$ , $a_2$ , $a_3$ ,..., $a_n$和m为正整数 , 又$a_1$|m , $a_2$|m ... $a_n$|m , 则m为$a_1$ , $a_2$ , $a_3$ ,..., $a_n$的公倍数.在$a_1$ , $a_2$ , $a_3$ ,..., $a_n$所有公倍数中 , 最小的那个公倍数为$a_1$ , $a_2$ , $a_3$ ,..., $a_n$的最小公倍数. 若m为$a_1$ , $a_2$ , $a_3$ ,..., $a_n$的最小公倍数 , 则{$a_1$ , $a_2$ , $a_3$ ,..., $a_n$} = m.

引理9 若a , b为正整数 , 而{a , b} = m . 若m'为a , b的公倍数 , 则m|m'.

引理10 若a , b为正整数 , 而{a , b} = m , (a , b) = d , 则ab = dm.

$\color{cyan}{算数基本定理}$

引理11 若整数a>1 , 则a定可以分成素因数的连乘积 , a = $p_1$ · $p_2$ · $p_3$ · ... · $p_n$ (n≥1).

引理12 若p为素数 , 则由p | 可得(p , a)=1 , 而当(p , a)=1时 , 可得p /| a.

引理14 若整数n≥2 , 而$a_1$ , $a_2$ , $a_3$ ,..., $a_n$和a为正整数. 当a|$a_1$ · $a_2$ · $a_3$ ··· $a_n$和(a , $a_1$) = (a , $a_2$) = ... =(a , $a_n$) = 1时 , 那么一定有a | $a_n$.

引理15 若a , b , c为正整数 , 而(a , b) = 1 , c|a , 则(b , c) = 1.

引理16 若a , b为正整数 , 而(a , b) = 1 , 则有(a , bc) = (a , c).

引理17 若整数n≥2 , 而$b_1$ , $b_2$ , $b_3$ ,..., $b_n$和a为正整数 , 当(a , $b_1$) = (a , $b_2$) =...= (a , $b_n$) = 1时 , 则有(a , $b_1$ · $b_2$ · $b_3$ ··· $b_n$) = 1.

引理18 若整数n≥2 , $a_1$ , $a_2$ , $a_3$ ,..., $a_n$为正整数 , 而p是一个素数 , 当p|$a_1$ · $a_2$ · $a_3$ · ... · $a_n$时 , 则至少存在有一个$a_r$能被p整除 , 也就是p|$a_r$.

引理19 若整数n≥2 , 而$p_1$ , $p_2$ , $p_3$ ,..., $p_n$和p为素数 , 当p|$p_1$ · $p_2$ · $p_3$ · ... · $p_n$时 , 则最少必有一个$p_r$ , 而r是1~n中的某一个数 , 它使得p = $p_r$.

定理1 (算数基本定理)若不计素因数的次序 , 则只有一种方法可以把一个大于1的正整数分解成素因数的连乘积.

第6章小数、分数和实数

分数化小数

引理1 设a , b都是正整数 , a < b而(a , b)=1. 若存在一素数p , 它使得p|b但是p/|10 , 则$\frac{a}{b}$一定不能化为有限小数. 若b= ${2}^{α}$ · ${5}^{β}$ , 其中α , β都是非负整数 , 则$\frac{a}{b}$能化为有限小数.

定义1 设${a}_{i}$(其中i = 1,2,3,...)是一个不大于9的非负整数. 若在0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···中任取出一个${a}_{j}$ , 那么一定存在一个大于j的正整数k , 使得${a}_{k}$ ≠ 0. 那么我们把0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···叫做一个无限小数.

定义2 若对于一个无限小数0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$··· , 能找出两个整数s≥0 , t≥0使得 ${a}_{s+i}$ = ${a}_{s+kt+i}$ , i = 1 , 2 , ... , t , k = 0 , 1 , 2 , ...成立 , 那么我们就称0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···为循环小数 , 并把0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···简单地记作0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{s}$ ° ${a}_{s+1}$ ··· ${a}_{s+t}$° .对于循环小数而言 , 具备以上性质的s及t不止一个 , 若找到的t是最小的 , 那么我们就称${a}_{s+1}$ , ${a}_{s+2}$ ,···, ${a}_{s+t}$为循环节；t为循环节的长度；若最小的s = 0 , 那么循环小数就叫纯循环小数. 若最小的s≥1 , 那么循环小数就叫混循环小数.

引理2 设0<a<b , 且(a , b)=1. 若$\frac{a}{b}$能表成纯循环小数 , 则我们有(b , 10)=1.

引理3 设0<a<b , 且(a , b)=1. 令h是一个最小正整数 , 能使${10}^{h}$≡1(mod b)成立 , 则$\frac{a}{b}$能表示成纯循环小数0.°${a}_{1}$···${a}_{h}$°.

引理4 设b是一个正整数且(10 , b)=1 , 令h是一个最小的正整数 , 能使${10}^{h}$≡1(mod b)成立 , 则有h | φ(b).

引理5 设a , b , ${b}_{1}$都是正整数 , a < b , (a , b)=1 , ${b}_{1}$ > 1 , (${b}_{1}$ , 10)=1. b = ${2}^{α}$ · ${5}^{β}$ · ${b}_{1}$ , 非负整数α , β不同时为0. 令h为最小正整数且能使${10}^{h}$≡1(mod ${b}_{1}$) , 则当α ≥ β时我们有$\frac{a}{b}$ = 0.${a}_{t}$ ··· ${a}_{α}$ ° ${a}_{α+1}$···${a}_{α+h}$° , 而当α < β时我们有$\frac{a}{b}$ = 0.${a}_{t}$ ··· ${a}_{β}$ ° ${a}_{β+1}$···${a}_{β+h}$°.

小数化分数

引理6 设0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···不能化为有限小数 , 也不能化成循环小数 , 则0.0.${a}_{1}$ ${a}_{2}$ ${a}_{3}$···${a}_{n}$···不能化成分数.