物理

[TINY NSD]TSHML 1st（二试）

仍旧原创

二试（满分180分，时间170分钟）

一、是否存在无穷项正整数列$\{a_n\}$，使得$\forall n \in \mathbb{N}^*$，$a_n \lt a_{n+1}$，$d(a_n) \lt d(a_{n+1})$，且存在正实数$C$，使得$\forall n \in \mathbb{N}^*$，$a_n \leq C \cdot 6^{\frac{n}{5}}$？其中$d(x)$表示正整数$x$的正约数个数。（40分）

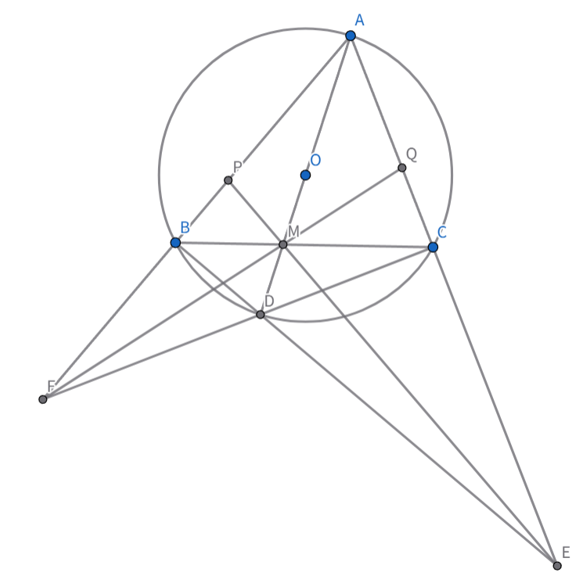
二、如图，四边形$ABDC$内接于圆$O$，$AD$为其直径，$AD$与$BC$交于$M$。延长$BD$，$CD$分别与$AC$，$AB$交于$E$和$F$，延长$FM$，$EM$分别与$AC$，$AB$交于$P$和$Q$。

（1）求证：$\frac{AB \cdot BF}{AC \cdot CE} = \frac{AQ \cdot BP}{AP \cdot CQ}$；

（2）若$\angle BAC = 60^\circ$，$P$、$O$、$Q$三点共线，求证：$AB = AC$。（40分）

三、已知$n \in \mathbb{N}^*$，$n \geq 3$，$a_1, a_2, a_3, \ldots, a_n$是$1, 2, 4, \ldots, 2^{n-1}$的一个排列，求$\sum_{i=1}^n \frac{a_i}{a_{i+1}}$的最小值，这里$a_{n+1} = a_1$。（50分）

四、小江和小海在玩游戏，小江在黑板上写了一个6进制的$n$位数，小海对这个数进行操作：每次操作时，选取其中的一位或相邻的若干位，在$\mod 6$意义下将它们同时加1或减1。对特定的$n$，求$f(n)$的最小值，使得无论小江写的数是多少，小海总能通过不超过$f(n)$次操作，将黑板上的数全部变为0。（50分）