物理 代数曲线集锦
本帖会介绍一些出现在高中数学中各种曲线。预计介绍:
- 卡西尼卵形线
- 笛卡儿叶形线
- 摆线
- 克莱因四次曲线
- $y=\ sin n\theta$
可配合Gerd Fischer的《平面代数曲线》使用,2,3,4会在其中有更深入介绍
$\huge{I.卡西尼卵形线}$
1.定义:
平面内到定点$F_1(−c,0), F_2(c,0)$距离之积为定值a2a2的点集(c>0)
2.标准方程:
原始方程:
$\sqrt{(x-c)^2 + y^2} \cdot \sqrt{(x+c)^2 + y^2} = a^2$
$(x^2 + y^2)^2 - 2c^2 (x^2 - y^2) = a^4 - c^4$ (1)
3.极坐标方程: $\rho^2 = x^2 + y^2$, $\tan\theta = \frac{y}{x}$,于是 $x^2 = \rho^2 \cos^2\theta$, $y^2 = \rho^2 \sin^2\theta$,代入方程 (1),得到:
$\rho^4 - 2c^2 \cos 2\theta \cdot \rho^2 + c^4 - a^4 = 0$
4.图像
定义$e = \frac{c}{a}$,当 $e \in \left(0, \frac{\sqrt{2}}{2}\right)$ 时图像如下
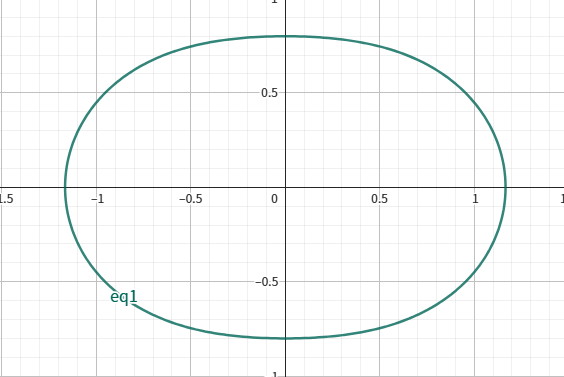
当 $e = \frac{\sqrt{2}}{2}$ 时,
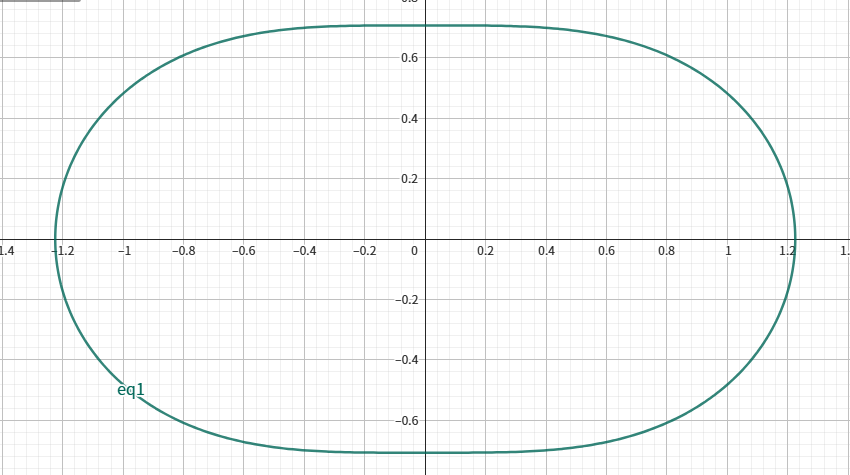
当 $e \in \left(\frac{\sqrt{2}}{2}, 1\right)$时,
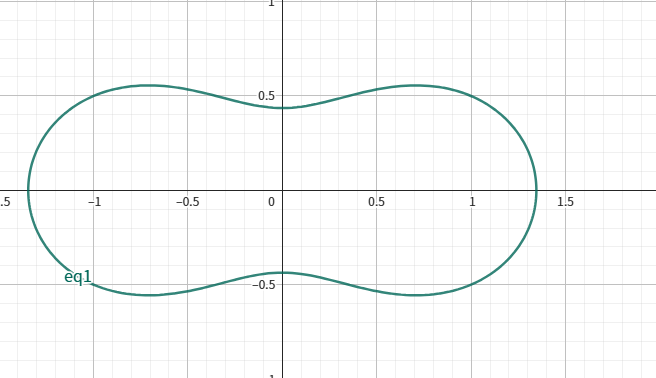
当 $e = 1$ 时
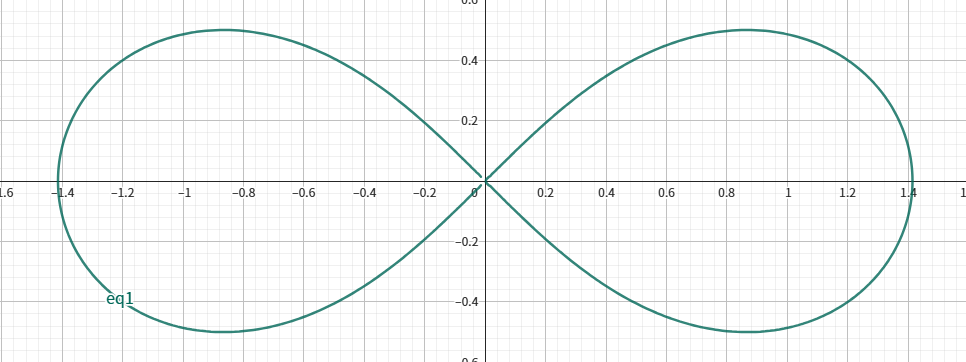
当 $e \in (1, +\infty)$ 时
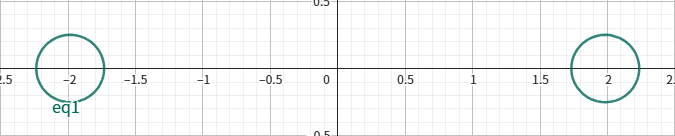
5.几何性质
1)$e=1$,曲线国原点,关于原点对称
2)定义域,值域
$S_{\triangle P F_1 F_2} = \frac{1}{2} |P F_1| \cdot |P F_2| \cdot \sin \angle F_1 P F_2=\frac{1}{2} |F_{1} F_{2}| \cdot |y| \leq \frac{1}{2} a^2$
于是$|y| \leq \frac{a^{2}}{2 c}$
同时$|x-c| \cdot |x+c| \leq a^2$,即有 $|x| \leq \sqrt{a^2 + c^2}$
3)极值
由 $(x^2 + y^2)^2 - 2c^2 (x^2 - y^2) = a^4 - c^4$,得:$y^2 = -(x^2 + c^2) \pm \sqrt{4c^2 x^2 + a^4}$(舍去负值)
设 $\varphi(x^2) = -(x^2 + c^2) + \sqrt{4c^2 x^2 + a^4}$,当 $\varphi'(x) = 0$,$x = \pm \frac{\sqrt{4c^4 - a^4}}{2c}$ 或 $x = 0$。
当 $e \in \left(0, \frac{\sqrt{2}}{2}\right)$ 时,图像有两个极值点,分别是 $\left(0, \sqrt{a^2 - c^2}\right)$, $\left(0, -\sqrt{a^2 - c^2}\right)$。
当 $e \in \left(\frac{\sqrt{2}}{2}, 1\right)$ 时,图像有六个极值点,分别是 $\left(0, \sqrt{a^2 - c^2}\right)$、$\left(0, -\sqrt{a^2 - c^2}\right)$、$\left( \pm \frac{\sqrt{4c^4 - a^4}}{2c}, \frac{a^2}{2c} \right)$、$\left( \pm \frac{\sqrt{4c^4 - a^4}}{2c}, -\frac{a^2}{2c} \right)$,其中,前两个是极大值点,后两个是极小值点。
当 $e \in [1, +\infty)$ 时,图像有四个极值点,分别是 $\left( \pm \frac{\sqrt{4c^4 - a^4}}{2c}, \frac{a^2}{2c} \right)$、$\left( \pm \frac{\sqrt{4c^4 - a^4}}{2c}, -\frac{a^2}{2c} \right)$,其中,前两个是极大值点,后两个是极小值点。当 $e=1$ 时 $(0,0)$ 也是极值点。


