物理

那些年，我们解过的微分方程

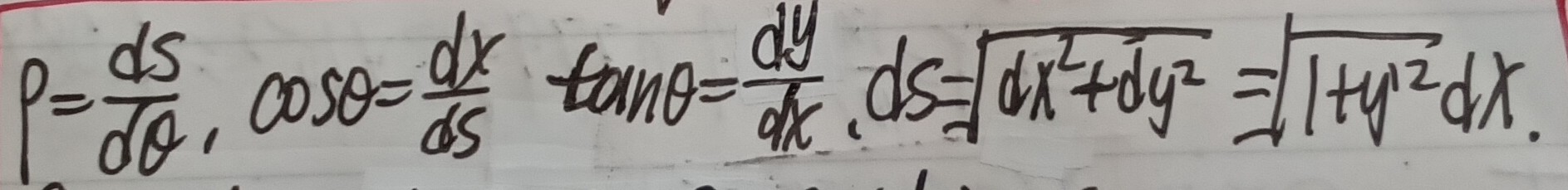
图示

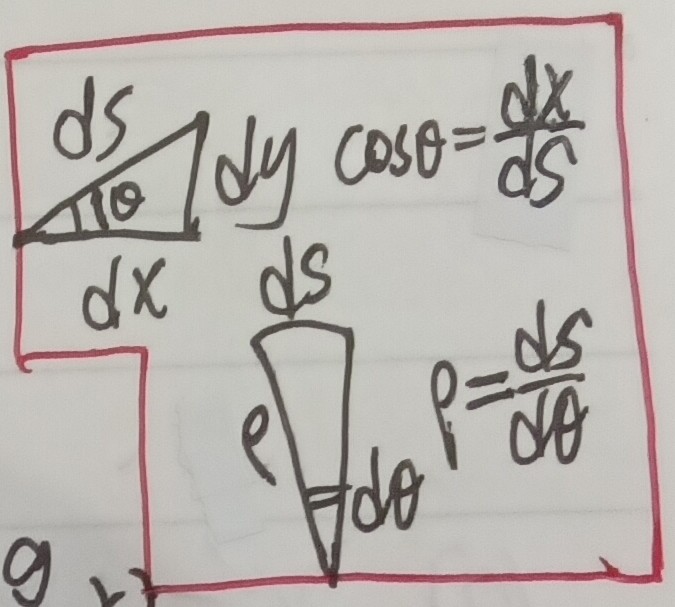
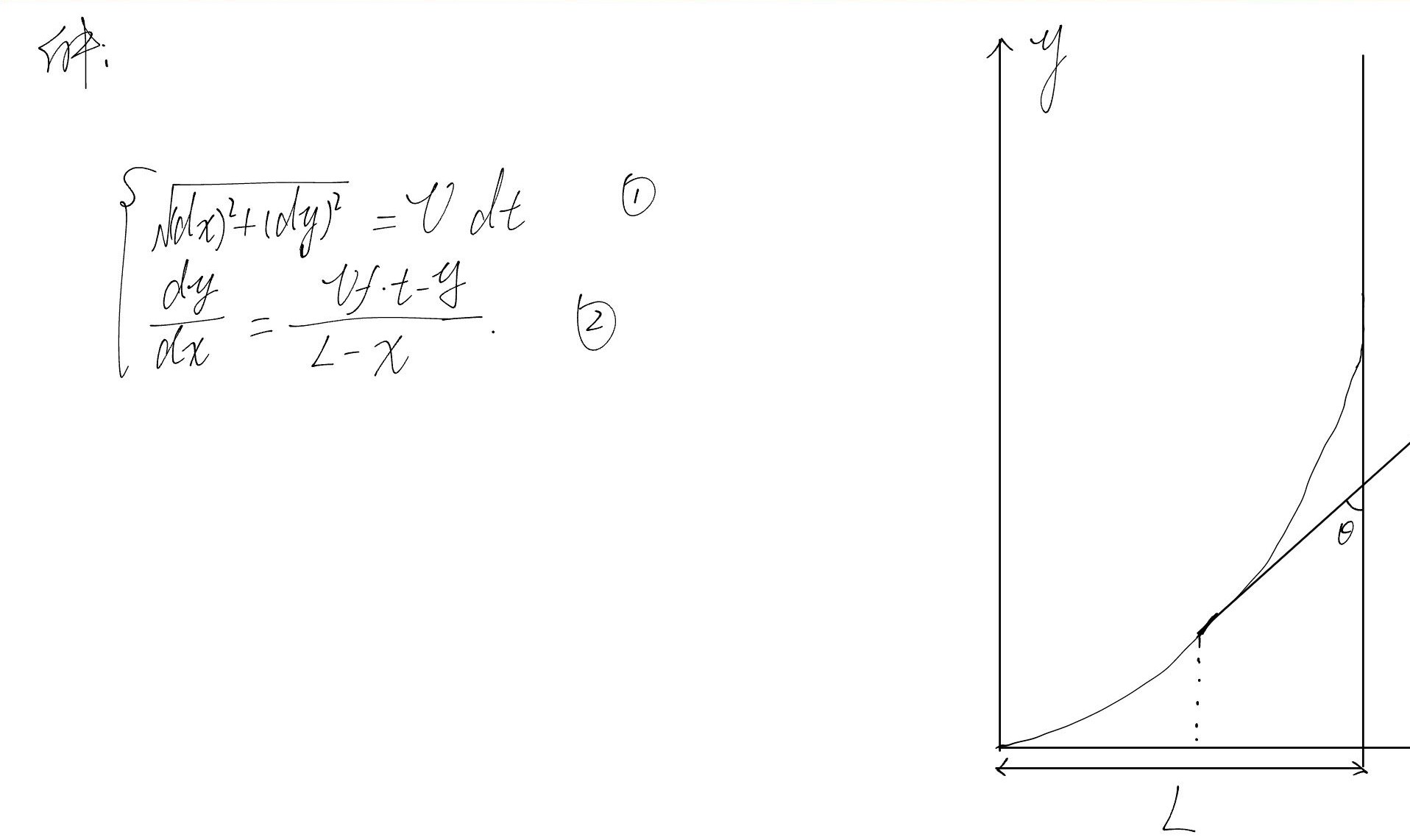
第二章：变质量相关

2.1 一阶线性微分方程的解法。

方程的普遍形式如下，在接下来的例题中我们将把动量定理化简为这个形式。

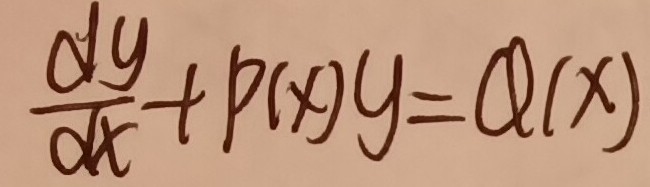
一般解法如下：

核心步骤在于乘以e指数项凑全微分。不过在下面的例题中我们会看到这一项的形式并不会太吓人，因为Q(x)很大概率是1/X形式的，这样不定积分结果是自然对数形式，于是再加在e指数上，便可以轻松的被化简。

例题2.1 熟悉的水滴？！下落问题

首先是针对水滴吸收所有沿途的雾气的条件：

第二个是我的写法，其实大差不差。标答的法一没有用微分方程，这里不做展示。法二跳步了，这是我的一个补充证明：

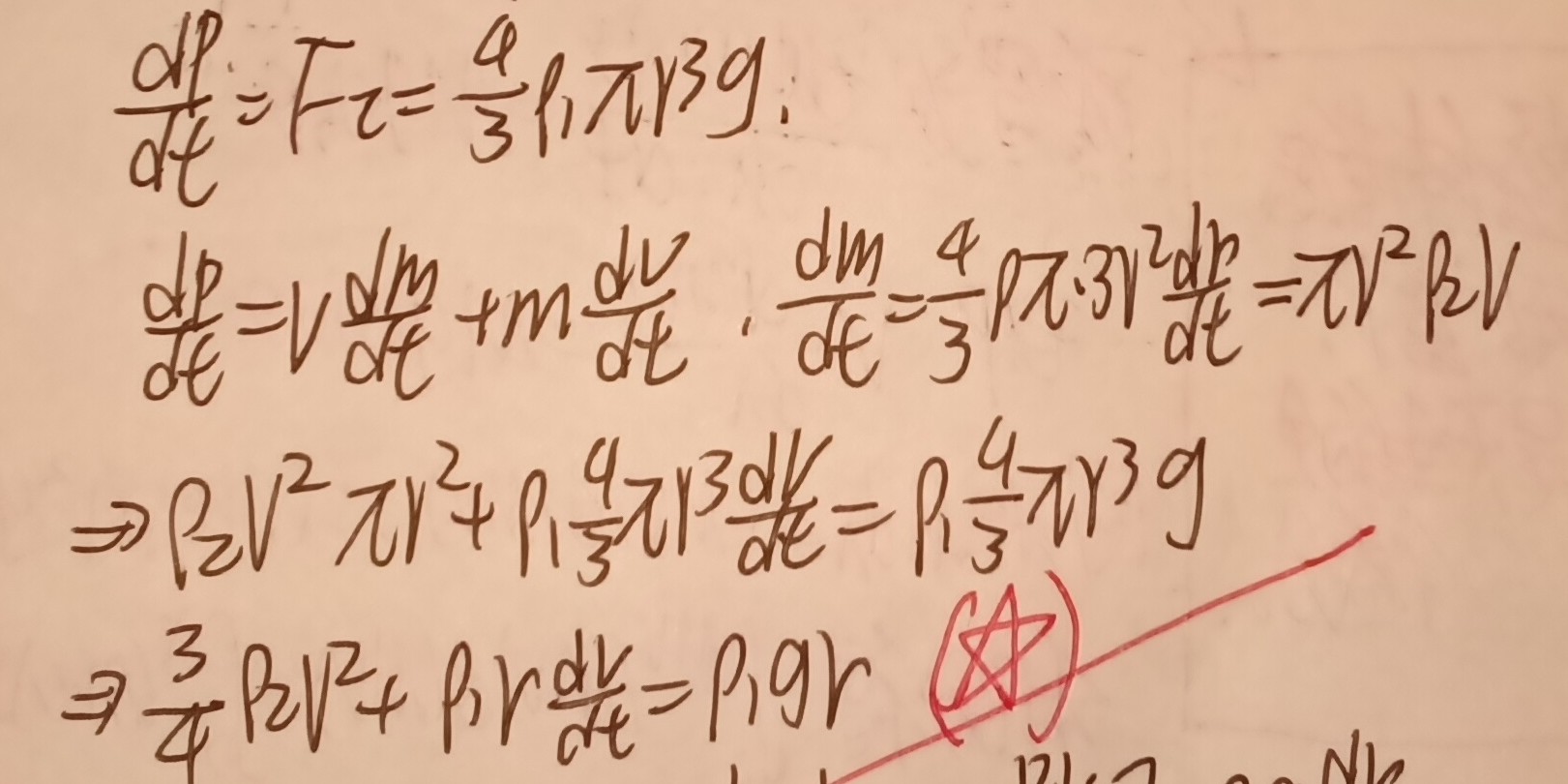
大体思路是把一堆r的两次方三次方消一下，整理一下系数。

然后这是我把答案抄写了一遍。我的书被画的比较乱就不拍书了。

但！是！我们怎么能容忍特解这种看起来像凑答案实际上就是在凑答案的行为呢？！虽然我证明了通解为0，但是这样做总是有些不爽，毕竟猜特解有点像抽奖，运气不好很费时间。这就要使用上文提到的凑全微分大法了：

请留意红框框出的换元，这同样是关键步骤之一，实现了不含时间项与降二阶为一阶的转化。

至于初始r0不为零的情况，我不会积🤣然后去请教了老师，这是他的答复

凑特解比较费时间，而这种全微分则是固定的套路，显然更具有优越性。

再来！例2.2 做过舒力的应该对舒老神奇的注意力有深刻印象。

直接上解析！过程和上一题大差不差。

至于为什么总是出现速度的平方，可以这样理解：对动量的微分会出现Vdm/dt，而很多时候dm/dt又是正比于V的，于是会出现V平方。对于一般的水滴，绳子，除非题目特别说明，都有这个性质。

但是，这时我们会发现这样的操作把时间隐去了。那么，需要求解X，V随时间的变化规律的时候，上述操作是否会失效？答案是：不一定！我们把V换成dx/dt接着积分就是。比如：

例2.3 尘埃中的盘子

先放标答：

很注意力是不是？很巧妙是不是？主播反正是想不到。

这是主播自己的另解。用我那个常规方法可以求得V～X关系，然后把V换成dx/dt便可以积得X~t关系。主播之前没看出来是因为乱设物理量，那个换元因子也设成了u（所以上述另解我设的是W），于是和地面系中速度u(t)搞混了，漏写了个平方，于是寄了（各位引以为戒）。可以看到这步积分只需简单换元一下，很容易。然后再求导，便得V～t关系。

三 .  天体运动之比耐方程

理论力学里的？超纲？不存在的，只需要角动量守恒和极坐标下受力展开式。

推导见图：

记不住没关系，主播自己也记不住。但是下面两个式子，尤其是第一个换元，是推导比萘公式的灵魂所在。这个必须要会！

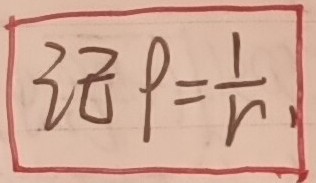
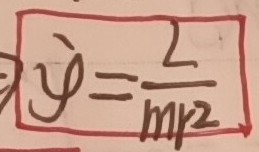
放俩例题，很好算的捏，也可以去看看菜源的索末菲原子模型，里面的推导用的也是比奈方程

比萘公式核心在于那一套对有心力的处理思路，公式本身并不重要。