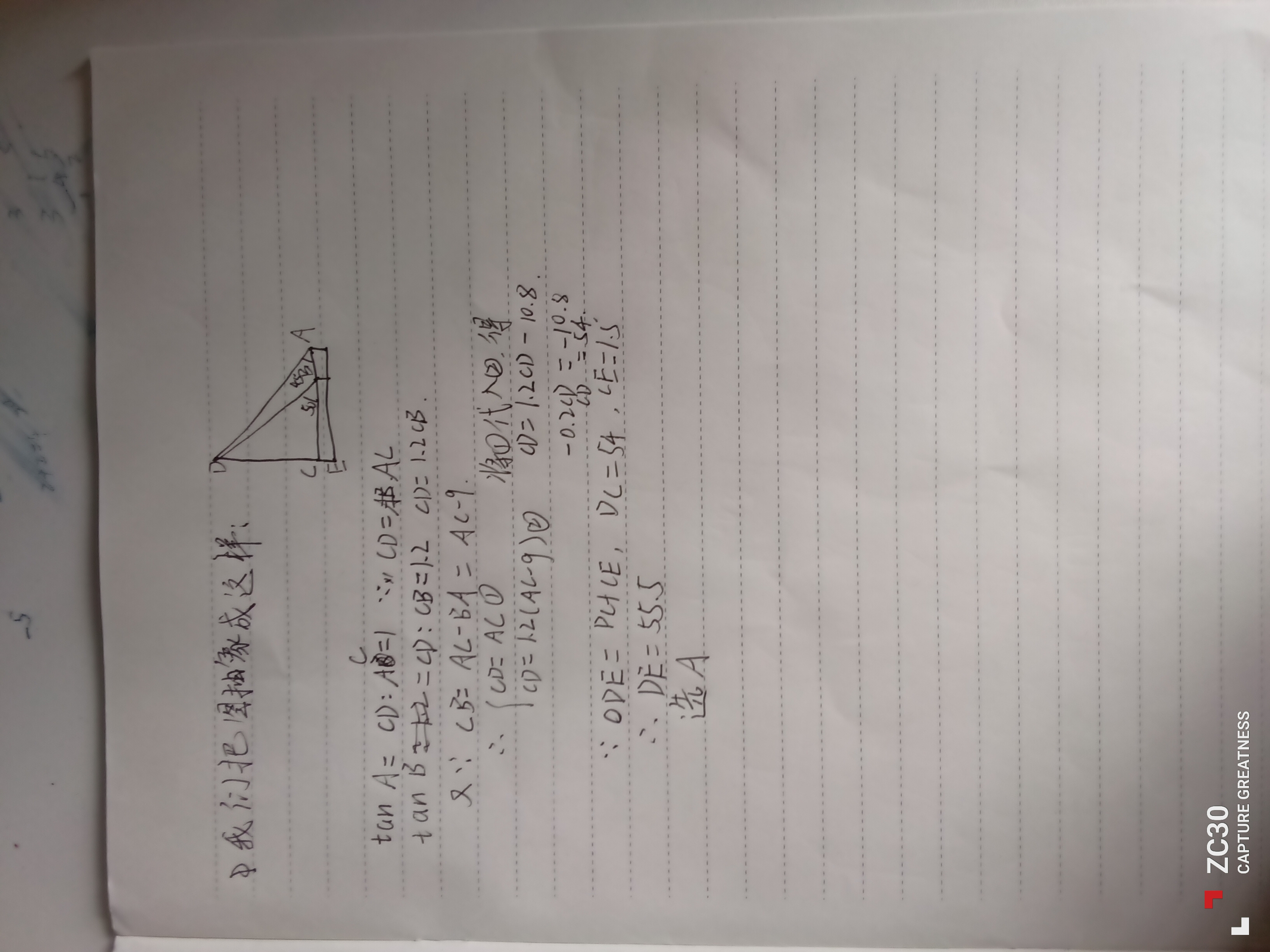共5条回复
时间正序
1条评论
- 1
世界是一个巨大的泰勒展开对吗
18小时前
$设塔高x米，则A点到塔的距离d_A=x-1.5米$
$所以\tan{50}=\frac{x-1.5}{d_B}=\frac{d_A}{d_B}=\frac{d_B+9}{d_B}=1.2$
$解得d_B=45，所以d_A=54米，故塔高55.5米，选A$
世界是一个巨大的泰勒展开对吗
14小时前
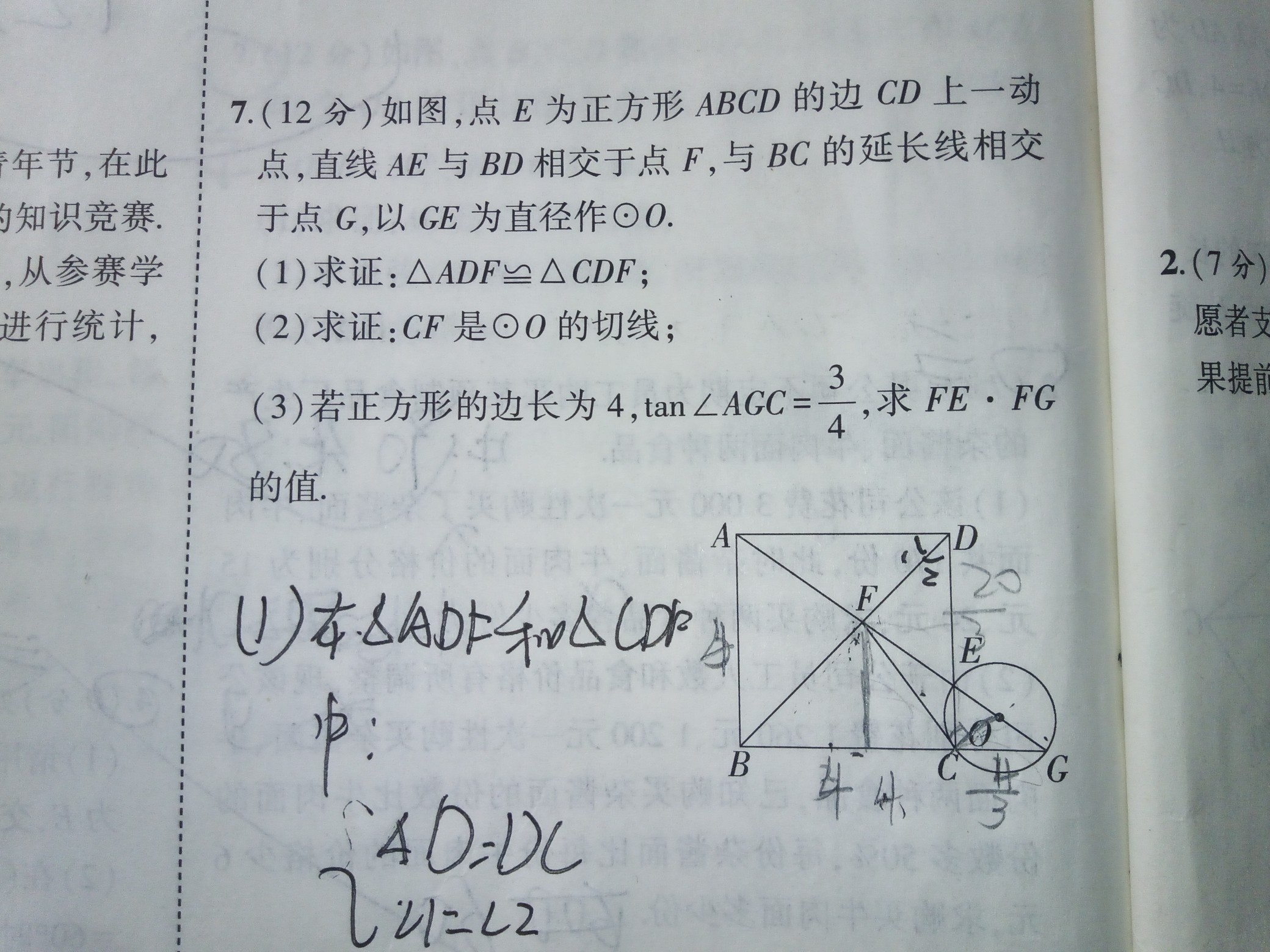
$$$(1)SAS全等$
$(2)连接oc，因为∠DAE+∠DEA=90^o，所以∠DCF+∠CEO=90^o，因为EO=OC=r$
$故∠DCF+∠DCO=90^o$即FC垂直CO，题目得证$
$(3)由\tan{AGC}=\frac{3}{4}及正方形边长是4可知$
$CG=\frac{4}{3}，CE=1，ED=3$
$由勾股定理得AE=5，圆半径r=\frac{5}{6}$
$设AF=a，FE=b$
$则\left\{\begin{matrix} a+b=5 \\ a^2+(\frac{5}{6})^2=(b+\frac{5}{6})^2\end{matrix}\right. $
$解得 \left\{\begin{matrix} a=\frac{20}{7} \\ b=\frac{15}{7}\end{matrix}\right.$
$因此，FE\cdot FG=\frac{15}{7} \cdot(\frac{15}{7}+\frac{10}{6})=\frac{400}{49}$
1条评论
世界是一个巨大的泰勒展开对吗
14小时前
忽略上边
$$$(1)SAS全等$
$(2)连接oc，因为∠DAE+∠DEA=90^o，所以∠DCF+∠CEO=90^o，因为EO=OC=r$
$故∠DCF+∠DCO=90^o$即FC垂直CO，题目得证$
$(3)由\tan{AGC}=\frac{3}{4}及正方形边长是4可知$
$CG=\frac{4}{3}，CE=1，ED=3$
$由勾股定理得AE=5，圆半径r=\frac{5}{6}$
$设AF=a，FE=b$
$则\left\{\begin{matrix} a+b=5 \\ a^2+(\frac{5}{6})^2=(b+\frac{5}{6})^2\end{matrix}\right. $
$解得 \left\{\begin{matrix} a=\frac{20}{7} \\ b=\frac{15}{7}\end{matrix}\right.$
$因此，FE\cdot FG=\frac{15}{7} \cdot(\frac{15}{7}+\frac{10}{6})=\frac{400}{49}$