物理

海朔·八水合过氧化钠对于芳香性的总结

最后一次更新：2025.8.2 01:34

更新了一点点稠环芳香性

-------------------------------------------------------------------分割线-------------------------------------------------------------------

由于过氧最近在论坛放了太多水，导致我的赞藏比从5：1爆涨到6：1

不行！不能再水了！为了降低论坛的水量，我选择

hhh开玩笑的

今天晚上，一个板砖（划掉）平板，一个过氧化物，我要更新化学！

-------------------------------------------------------------------分割线-------------------------------------------------------------------

芳香性最初发现于苯（benzene）及其衍生物，当时是用来描述它们特殊的气味以及易取代不易加成的特性

但现在，芳香性的定义已经与气味无关

具有芳香性的物质有特殊的、出乎意料的稳定性

举一个老掉牙的例子

众所周知，烯烃的加氢过程是放热的，而1，3-环己二烯可以在高温脱氢生成苯，这个反应居然会放出一些热量！

什么物质具有芳香性？芳香性物质具有什么特殊的性质？为什么？这样特殊的稳定性有强弱之分吗？如果有，为什么？

这就是本文要讲的内容

$Huge{一、芳香性（Aromaticity)的判定}$

在介绍芳香性之前，首先要介绍一下反芳香性（antiaromaticity）与无芳香性（non-aromaticity）

一般来说，需要我们讨论芳香性的物质有以下几个特点：

1）有含有共轭双键的环系结构

2）环上每个原子皆有未杂化的p轨道

3）这些轨道形成了一个连续、重叠、平行轨道的环系（因此这些环一般是平面的）

有芳香性的物质往往有这些特点，并且π电子完全离域使物质比开链的稳定

同样，具有类似结构的共轭体系，若成环比不成环稳定，则成环的有芳香性

有反芳香性的物质往往也有这些特点，π电子也完全离域，但这使物质变得比开链的不稳定

同样，具有类似结构的共轭体系，若成环比不成环不稳定，则成环的有反芳香性

而无芳香性的物质没有全部满足这些特点，不会使物质的稳定性发生改变

1、分子轨道理论（Molecular Orbital Theory）（以下简称MO），最朴素的芳香性判定方法

化学中的理论千千万，然而如果想用它们去解释实验事实，能用的恐怕一个手都能数得出来

就比如我们想解释苯很稳定，而环丁二烯（cyclobutadiene）很活泼时，好用的共振论就突然不香了

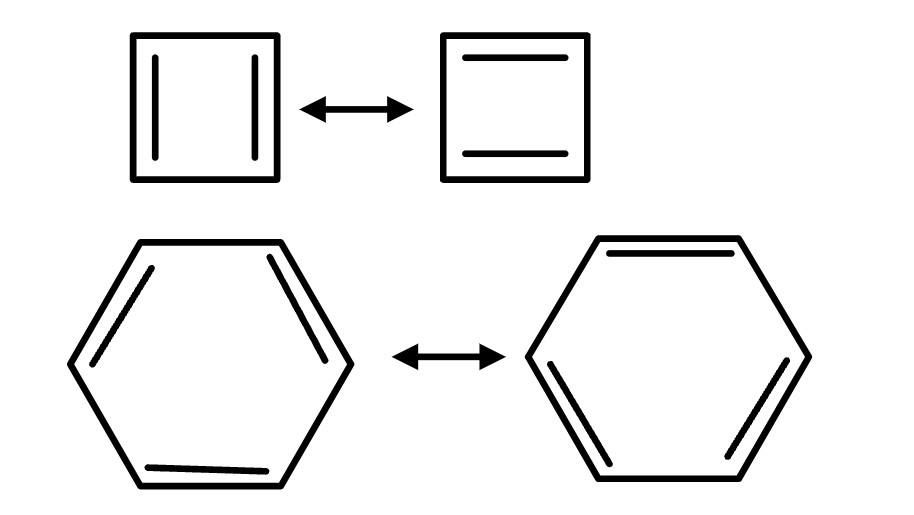
可以看到，苯和环丁二烯的共振式非常像，所以不能使用共振式来解释这个事实

但我们可以使用MO来解决这个问题

我们可以很容易地画出苯和环丁二烯的MO:（图片来源：210讲义）

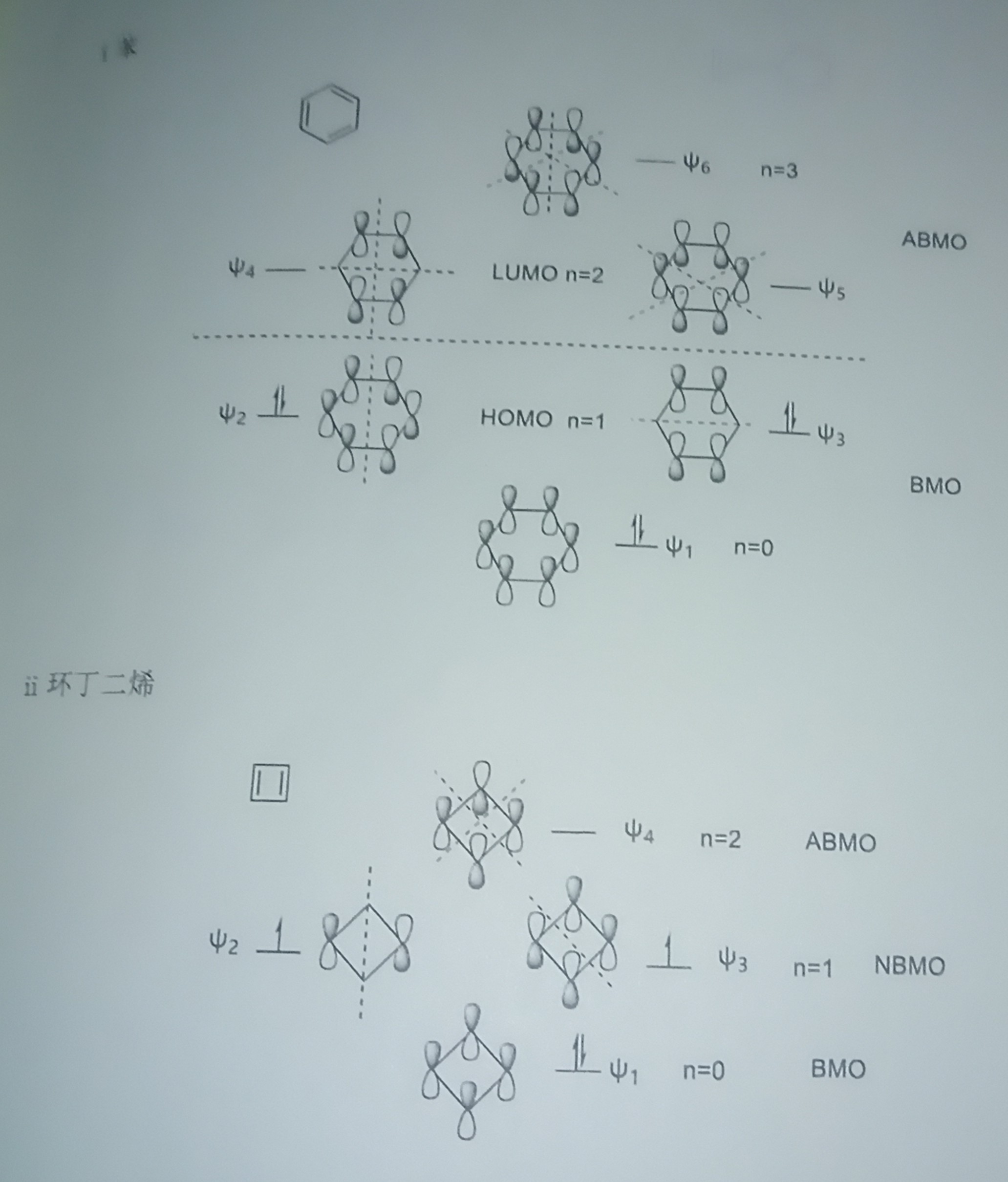
从中可以发现，苯的6个π电子填满了苯分子的成键轨道（Bonding Molecular Orbital）（BMO）

而环丁二烯占满了BMO，非键轨道（Non-bonding Molecular Orbital）（NBMO）半满，两个非键轨道各有一个单电子

这单电子就很令环丁二烯难受，这两个轨道作为HOMO，环丁二烯有一种极强的倾向去丢掉这两个轨道上的电子，或接受两个电子使它们全满

这就使环丁二烯远远不如苯稳定

我们可以画出苯和开链的己三烯的MO:（图片来源：巨本）

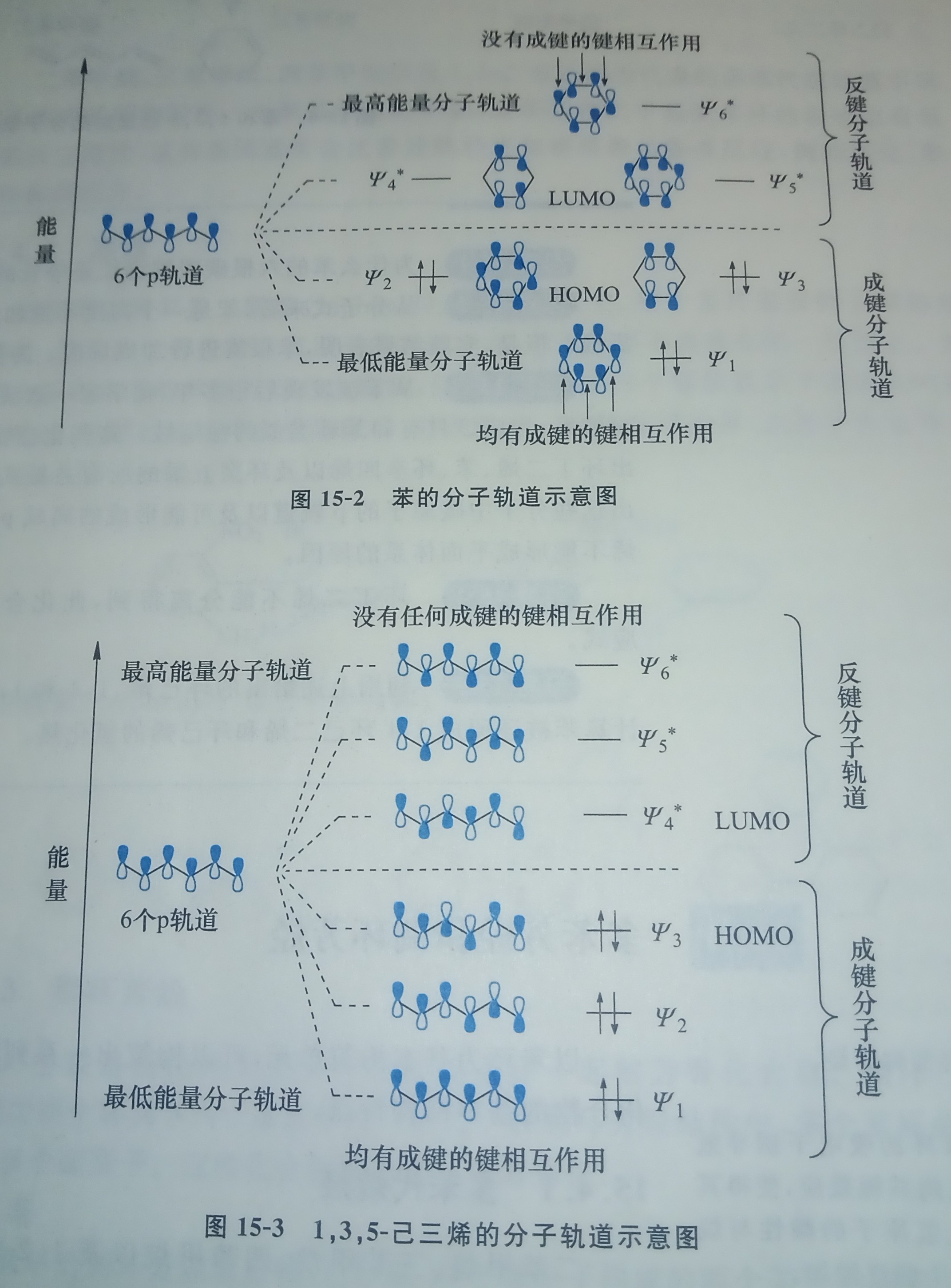
可以发现，苯的Ψ1，Ψ2比己三烯的Ψ1，Ψ2能量低，苯的Ψ3比己三烯的Ψ3的能量略高

总的来说，苯的MO的能量比己三烯的低不少

根据芳香性的定义，苯具有芳香性

同样也可以写出环丁二烯和开链丁二烯的MO（过氧懒得画了）

可以发现环丁二烯NBMO上的两个单电子严重抬高了环丁二烯MO的能量

使环丁二烯的稳定性不如开链的丁二烯

所以环丁二烯具有反芳香性

回到第一张图，可以发现，若想使这样的分子有芳香性，则它们的BMO或BMO+NBMO必须全满

而这样的分子中，根据MO的思想，BMO总是有奇数个

设有2n+1个，则占满BMO及BMO+NBMO所需要的π电子数可以分别表示为4n+2和4(n+1)+2（n为任意正整数）

由于n是一个正整数，所以n+1也是正整数，4(n+1)+2也是一种4n+2

如果想使这样的分子有反芳香性，则它的HOMO（可以在NBMO或ABMO）必须半满

则它的π电子数可表示为4(n+1)或4(n+2)（n为任意正整数）

这两种情况都可以表示为4n

总结一下，有4n+2个π电子的平面环状共轭体系有芳香性，有4n个π电子的有反芳香性，若分子没有平面环状共轭体系则无芳香性

2、Huckel规则----------判断平面环状共轭体系为芳香性or反芳香性的捷径

1931年，E.Huckel（休克尔）提出了一条芳香性判断规则-----------著名的Huckel规则（不得不说Huckel是真的厉害）

Huckel规则是判断轮烯（annulene）及其类似物与衍生物的捷径

由于它是一条经验规则（当年MO都没有被提出），所以被判断的物质必须含有平面环状共轭体系

该规则认为，在这样的物质中，具有4n+2个π电子的具有芳香性，具有4n个π电子的具有反芳香性

该规则的本质就是之前讲的MO

现在我们来判断几个物质是芳香性or反芳香性or无芳香性

（1）苯：6个π电子，4n+2，无需多言

苯的碳碳键角是完美的120°，也是它如此稳定的另一个原因

（2）环丁二烯：4个π电子，4n，反芳香性

事实上，环丁二烯为了削弱反芳香性，其分子结构为长方形，π电子未完全离域

环丁二烯不稳定的另一个原因是极大的环张力

它很活泼，寿命只有5秒

但以环丁二烯作为π配体的物质还是可以稳定存在的，比如$Fe(CO)_3(η^4-C_4H_4)$

在这个配合物中，环丁二烯带两个负电荷，具有芳香性

（3）环辛四烯：8个π电子，4n，反芳香性？无芳香性！

为什么是无芳香性呢？因为环辛四烯不是平面分子

为了防止反芳香性并减轻双键的大环张力，它采取了澡盆型的构型

它的化学性质与普通的烯烃无异，可以正常被高锰酸钾氧化，被溴加成，发生 Diels-Alder反应

但如果向里面加钠！！！加加加加加到厌倦！！！或者使用五氟化锑＋氟氯化砜氧化

可以分别得到环辛四烯的双负离子与双正离子

这两个离子分别有10个和6个π电子，均具有芳香性

（4）两种[10]－轮烯：4n+2，但不共平面，无芳香性！

[10]－轮烯有两种代表性的异构体：（如图所示）

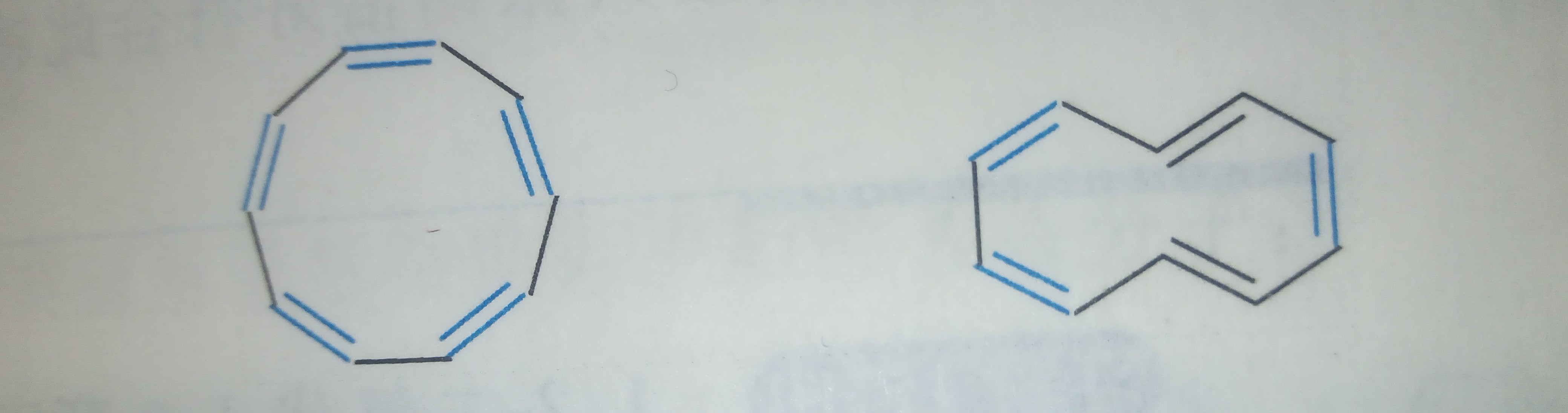
由于大环张力，第一种[10]－轮烯不能使所有碳原子共平面，就没有芳香性

第二种[10]－轮烯由于内氢重叠，很不稳定，容易被氧化生成萘（naphthalene）或对旋关环

但是，如果把这两个氢换成一个亚甲基，就可以避免内氢的空阻，得到芳香性的物质

这种改进方法也适用于其他内氢重叠的4n+2轮烯

（5）更大的4n轮烯

由于环的扩张，环的刚性减小，这样的轮烯为避免反芳香性，会弯曲生成无芳香性的物质

（6）更大的4n+2轮烯

除了一些像之前介绍的内氢重叠的轮烯，更大的4n+2轮烯均有芳香性

（7）茂负离子（cyclopentadienyl anion）

环戊二烯基负离子，简称茂负离子，有6个π电子，有芳香性

不仅如此，它的键角为108°，很接近120°，也是它稳定的另一个原因

它和铁可以形成非常稳定的夹心配合物----------著名的二茂铁（ferrocene）

二茂铁是橙黄色固体，其分子高度对称，十根碳-铁键的键长均相等

该化合物具有极高的热稳定性与化学稳定性，可以发生芳烃发生的反应

注意！茂负离子虽然稳定，但也跟正常的负离子一样，具有亲核性

茂负离子显强碱性，会正常地与水反应

（8）䓬正离子（tropylium cation）与环丙烯正离子

环庚三烯基正离子，简称䓬正离子，可以通过用稀硫酸处理环庚三烯醇来制备，有6个π电子，有芳香性

一个重要的类似物质（也是䓬正离子的词源）叫做䓬酚酮（2-羟基-2,4,6-环庚三烯-1-酮）

该物质可以形成分子内氢键，氧这边略带负电，环庚三烯环略带正电，形成芳香性的䓬正离子

该物质的化学性质很像苯酚

环丙烯正离子，是最小的芳香性体系，有2个π电子，有芳香性

注意！它俩也有碳正离子的通性：强的Lewis酸性和亲电性

然而，Huckel规则不是万能的，有些东西是这条规则解释不了的

3、Hückel规则判断不了的芳香性

由于Hückel规则是一条经验规则，它只能判断轮烯及其类似物的芳香性

如果我们想要判断的分子不是轮烯及其类似物，这条规则就显得有些无能为力了

接下来过氧要介绍同芳香性、稠环芳香性、富瓦烯类化合物的芳香性、杂环芳香性

甚至更加神奇的球面芳香性、Möbius芳香性、以及突破芳香性定义的Y芳香性和σ芳香性等等

（1）同芳香性（homoaromaticity）

在研究芳香性的过程中，科学家们发现：

有些环状化合物的共轭体系虽然被一个或更多sp³碳所打断，但仍然有一些特殊的物化性质

这个现象表明，这样的π共轭体系的中断处可谓藕断丝连，仍然通过p轨道的重叠使共轭体系得以延续

这就使这样的体系仍然有类似芳香性体系的特殊物化性质

于是，S.Winstein就在研究3-二环[3.1.0]环己基正离子时提出了同芳香性的概念

此后，该概念迅速发展

如今，同芳香性成为了一种特殊的芳香性，存在于被一个或多个sp³碳打断的的共轭体系中

同芳香性的产生基于同共轭效应，这种效应就是刚才所说的共轭体系通过p轨道的重叠使共轭体系延续

这种重叠非常特殊，可以跨越一个或几个sp³碳，其重叠力度介于σ键与π键之间

通过这样的重叠就可以形成一个类似平面共轭轮烯的体系，就可以使用Hückel规则进行判断了：

如果有4n个π电子在同芳香性体系中共轭，则该体系具有同反芳香性

如果有4n+2个π电子在$同芳香性体系$中共轭，则该体系具有同芳香性

1995年，R.F.Childs等人提出了同芳香性的基本标准：（以下内容来源于巨本）

1）体系中必须有一个或多个同共轭作用

2）同共轭作用应当比较显著，对于有σ键的同芳香性应具有部分键级，对于空间作用而言，同芳香性则必须有明显的空间相关作用

3）体系中电子的离域应当使化合物产生类似芳香性的特征，如键长平均化、π轨道的有效重叠、正／负电荷的分散以及键级的变化

4）符合4n+2规则

5）由同芳香性产生的稳定化能应不小于8.4kJ·mol⁻¹

（这一条很重要，因为同共轭次数越多，中间的sp³碳就越多，同共轭效果就越差，直到稳定化能小于8.4kJ·mol⁻¹而不能形成同芳香性体系）

6）具有芳香化合物的磁学性质（过氧以后会讲）

这条规则已经被科学家普遍接受，同芳香性的研究也从正离子推广到更多物质

（2）稠环化合物的芳香性及强弱比较

轮烯可以通过各种方式并接，形成稠环化合物，这些化合物的结构不符合Hückel规则的判断前提，所以不能直接使用它来判断此类物质的芳香性

1）仅有苯环的稠环化合物的芳香性及其比较 Clar规则

苯作为一种轮烯和六边形分子，可以像铺瓷砖似的以多种方式并接

苯有芳香性，所以这样的化合物肯定有芳香性，但π电子不一定符合4n+2规则

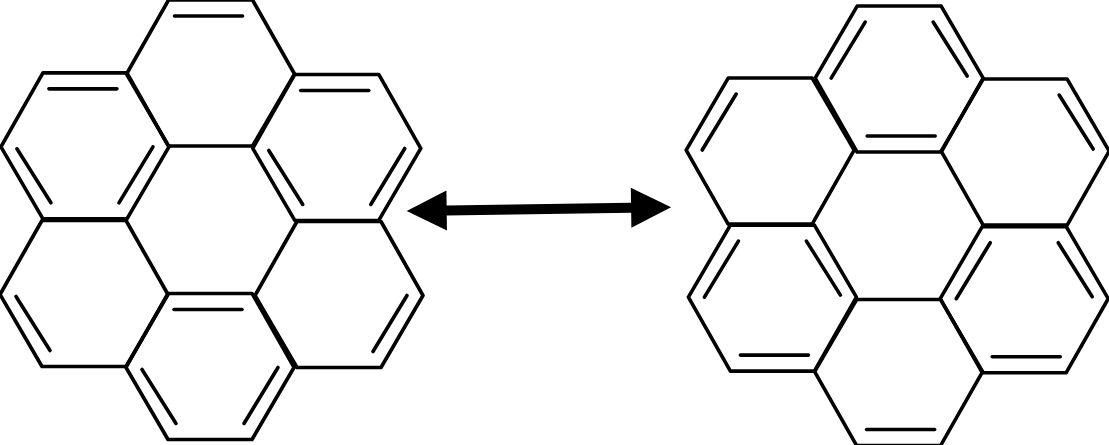
比如芘有16个π电子，蒄有24个π电子

但事实上，它俩都很稳定

如果我们想要判断这样的化合物的整体芳香性，只需要看最外面的一个大环就行了

比如芘最外面的大环有14个π电子，蒄最外面的大环有18个π电子，均符合Hückel规则

所以它们具有芳香性

但是！这类物质的稳定性差异很大！

比如同为有七个苯环的芳烃，蒄像一面盾牌，稳如磐石，而并七苯很活泼，很容易被各种氧化剂氧化

为什么呢？我们可以使用共振论来解释：

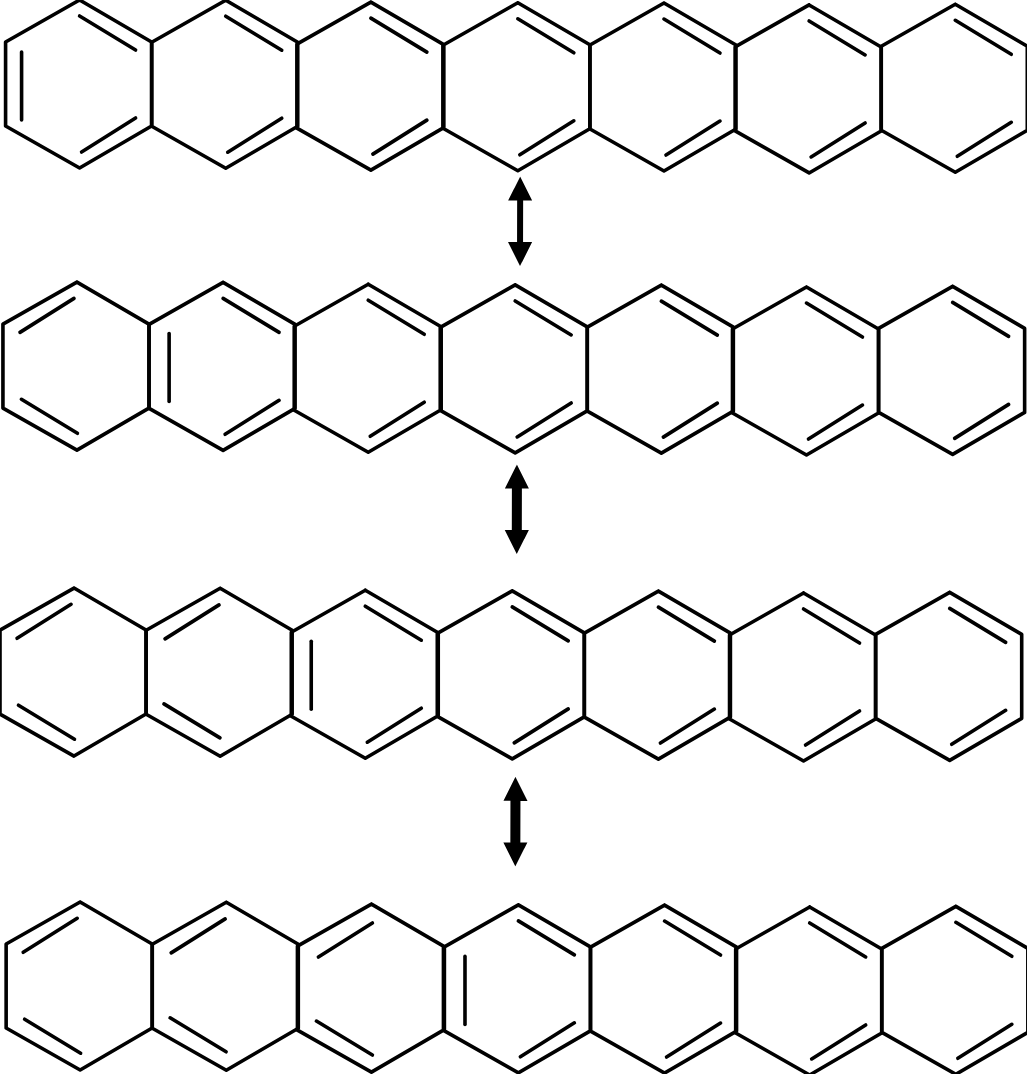
可以发现，并七苯无论在哪个共振式中，都只有一个完整苯环，而稳定的蒄在每个共振式中，都有三个完整苯环

这就解释了这两种物质的稳定性差异

波兰化学家Erich Clar整合实验数据以及理论分析，提出了以这种比较方法为基础的Clar规则

未完待续……