物理

[中考]锐评广东2025中考数学

帖主要润了，欢迎讨论，但是不要指望帖主回复你。

“出题人到底想干什么，话都说不清楚😅👎。”——我的竞赛教练

这里是向量vector，今天我们就来锐评一下2025年最烂的大考卷子。其ex程度恐怕是高考的114514倍。

学习飘零哥哥，先说结论：就这垃圾还有人说出的好啊，什么玩意，后三题跟废题一样。出题人的语焉不详导致这张卷子出现了一个很南蚌的问题：考的好的人不见得多么有实力，考的不好的人不见得实力不强。而且这并不是一个偶然的现象。有些人真的就是靠运气(比如把最小勾股数直接猜了出来)和若有若无的attention考到了高分，这真的能考察到基本功和思想吗？这张卷子出的质量居然还不如某校自主招生？我的评价是做高中题就老实了。

先看看这张卷子的双压轴吧：(感谢@爱数物的5汉提供的题干，大家可以去看看他在这个帖子内对于勾股数通项的推导)

22第一问和送分就没什么区别，主要是第二问很南蚌。代数形式？那我问你，我写含有两个未知数的式子，你准备怎么给分？

有些同学看到这道题(根据我的采访，而且这哥们不菜)的反应是这样的：勾股数通项？😨→让我想想🤔→那我就写两个未知数🤓☝️→嘿嘿秒了😋。

bro......如果这道题真的可以随便用两个未知数表示那这也太水了吧。其实这道题问的是本原勾股数的通项，不是让你随便写一个式子啊。如果你写出的式子含有两个未知数(比方说x和y)，你要如何证明由你的式子产生的勾股数就是所有的勾股数呢？也就是说，如果你的式子不能产生一些本原勾股数，那你的答案还对吗？首先我们先不提一部分同学写的什么x^2+y^2，2xy之类的东西到底能不能覆盖勾股方程(a^2+b^2=c^2)的所有根，就算真的可以，没几个人在考场上证的出来。

勾股方程本来就要涉及初等数论的知识才能解，而在考场上求它的解首先要把整除理论和其基本性质说明一遍，光是这个过程就已经远远超纲了。(答题卡太小了不一定写的下——Fermat笑传之中考猜猜悲)而且你的结论都不一定是对的......如果你给出的生成方式真的不能覆盖呢？实际上，一般来说考生给出的答案都是不能覆盖的......

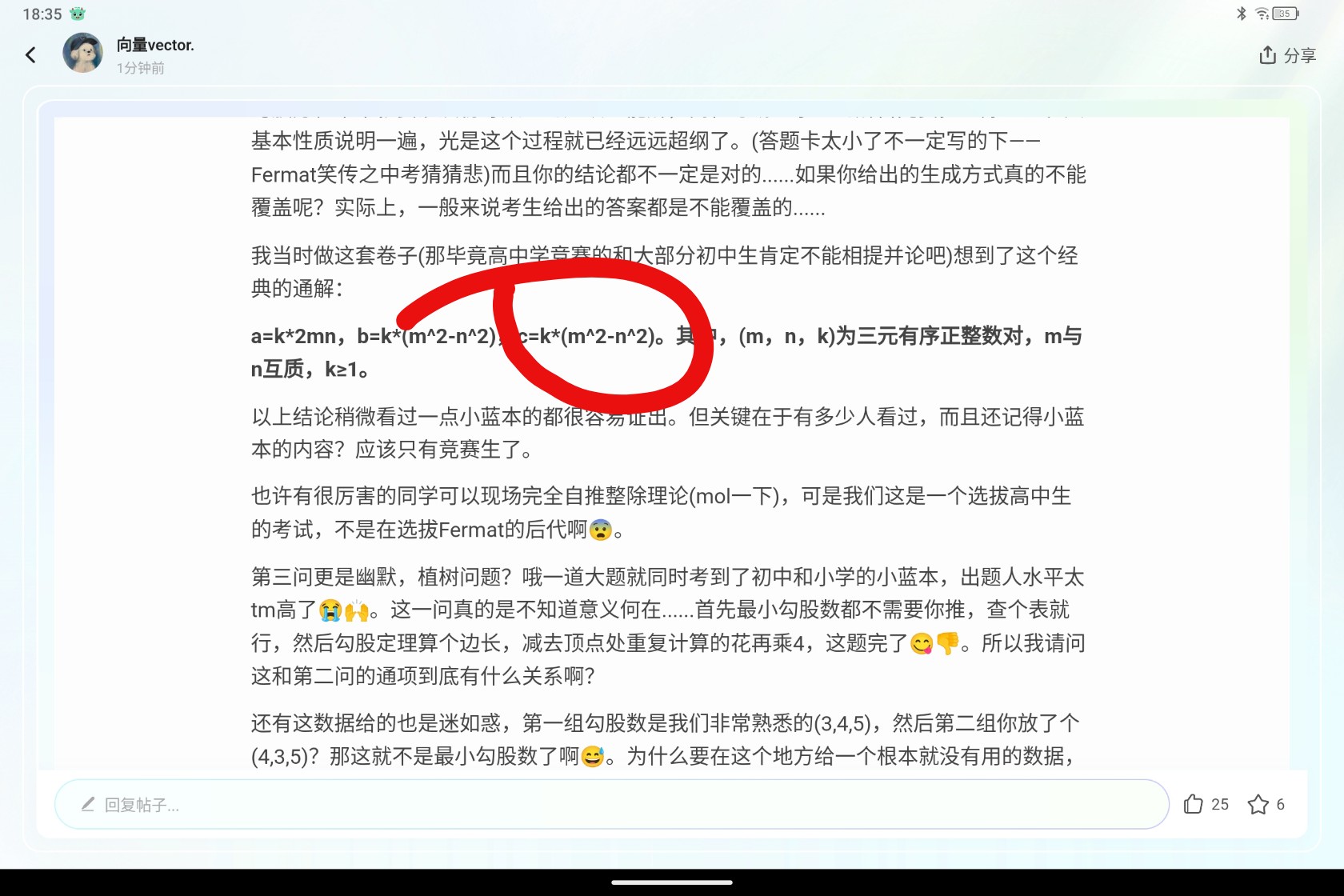
我当时做这套卷子(那毕竟高中学竞赛的和大部分初中生肯定不能相提并论吧)想到了这个经典的通解：

a=k*2mn，b=k*(m^2-n^2)，c=k*(m^2+n^2)。其中，(m，n，k)为三元有序正整数对，m与n互质，k≥1。

以上结论稍微看过一点小蓝本的都很容易证出。但关键在于有多少人看过，而且还记得小蓝本的内容？应该只有竞赛生了。

也许有很厉害的同学可以现场完全自推整除理论(mol一下)，可是我们这是一个选拔高中生的考试，不是在选拔Fermat的后代啊😨。

第三问更是幽默，植树问题？哦一道大题就同时考到了初中和小学的小蓝本，出题人水平太tm高了😭🙌。这一问真的是不知道意义何在......首先最小勾股数都不需要你推，查个表就行，然后勾股定理算个边长，减去顶点处重复计算的花再乘4，这题完了😋👎。所以我请问这和第二问的通项到底有什么关系啊？

还有这数据给的也是迷如惑，第一组勾股数是我们非常熟悉的(3,4,5)，然后第二组你放了个(4,3,5)？那这就不是最小勾股数了啊😅。为什么要在这个地方给一个根本就没有用的数据，然后让看到的考生犯错导致第二问求错？没活整了可以去咬打火机(好像我评价25高考一卷时也说了这句话😋)。