物理

预备轮之几何

三角形篇:

一、三角形基本概念与性质

1、三角形的内角平分线上的点到这个角的两边的距离相等，同一个三角形中，大角的角平分线短于小角的小平分线

2、三角形中任意一边上的中线都把三角形分成面积相等的两部分，同一个三角形中，大边上的中线短于小边上的中线

3、三角形的任意一边上的高都垂直于该边，三角形的三条高未必都在三角形内部

4、三角形的内角平分线，中线，高，和边的中垂线又有相同之处:在同一个三角形中，三条中线，或者三条高，或者三条内角平分线，或者三条边的中垂线，它们分别相交于一点（三线共点，由塞瓦定理可证明）

5、三角形顶角的平分线与底边上的高所夹的角等于两个角差的一半

6、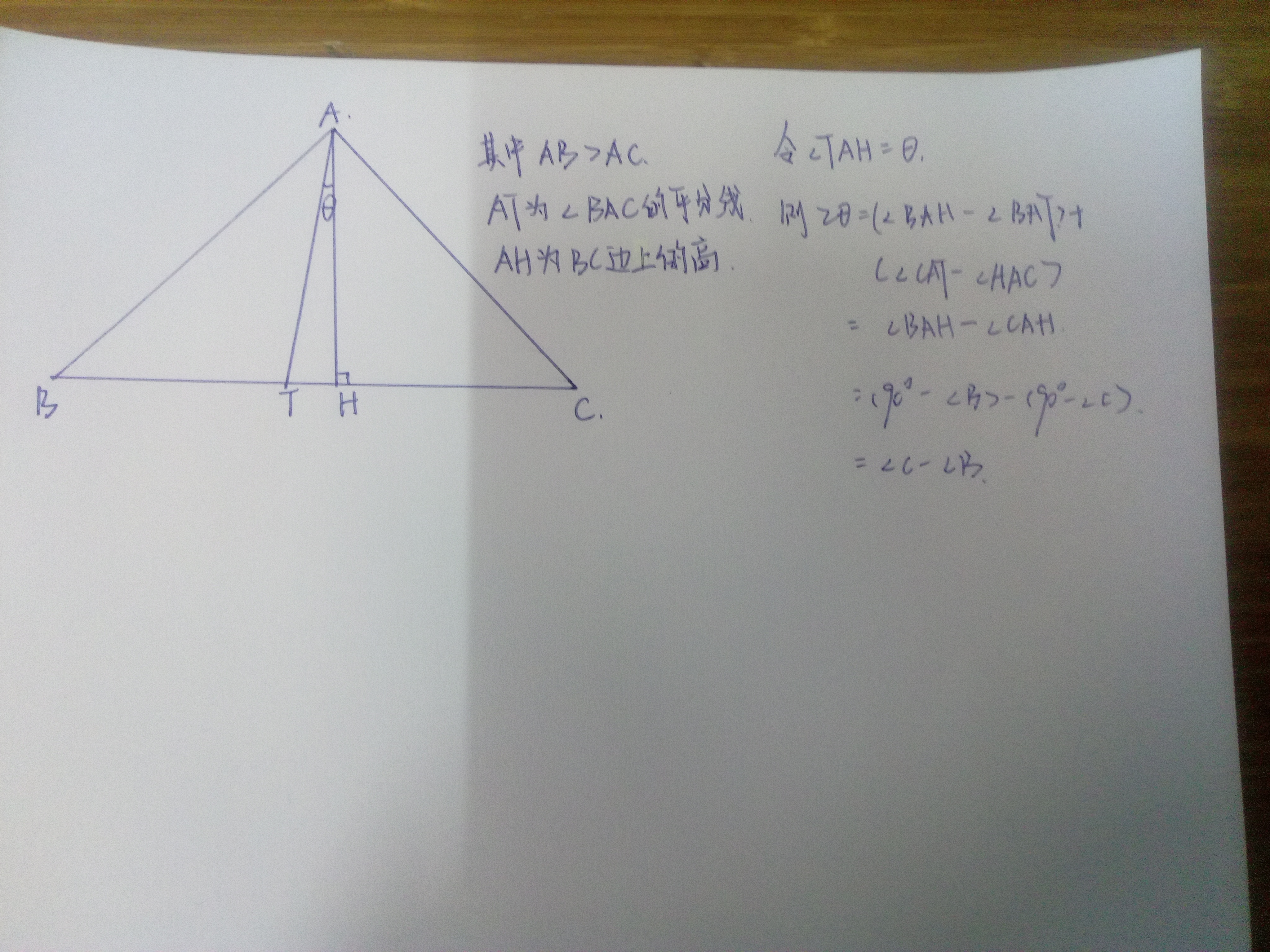7、在不混淆的情况下，有时，三角形的角平分线，中线和高也指他们所在的直线

二、三角形面积

1、普通求法:S=1/2ah

2、三角函数求法:S=1/2absin∠C

3、海伦公式:记p=1/2（a＋b＋c）

则S=根号下p（p－a）（p－b）（p－c）

余弦定理证法:

双勾股证法:

特别感谢@妄想徒手摘星

由上可知:

1、等底等高的两个三角形面积相等

2、两个等底的三角形面积比等于底边上对底高的比

3、两个等高的三角形的面积比等于他们底边的比

三、三角形的角平分性质定理与外角平分线性质定理

三、正弦定理与余弦定理

1、正弦定理:a/sin∠A=b/sin∠B=c/sin∠C=2R

2、余弦定理:$a^2$=$b^2$＋$c^2$－2bc cos∠A

                        $b^2$=$a^2$＋$c^2$－2ac cos∠B

                        $c^2$=$a^2$＋$b^2$－2ab cos∠C

四、共边比例定理与共角比例定理

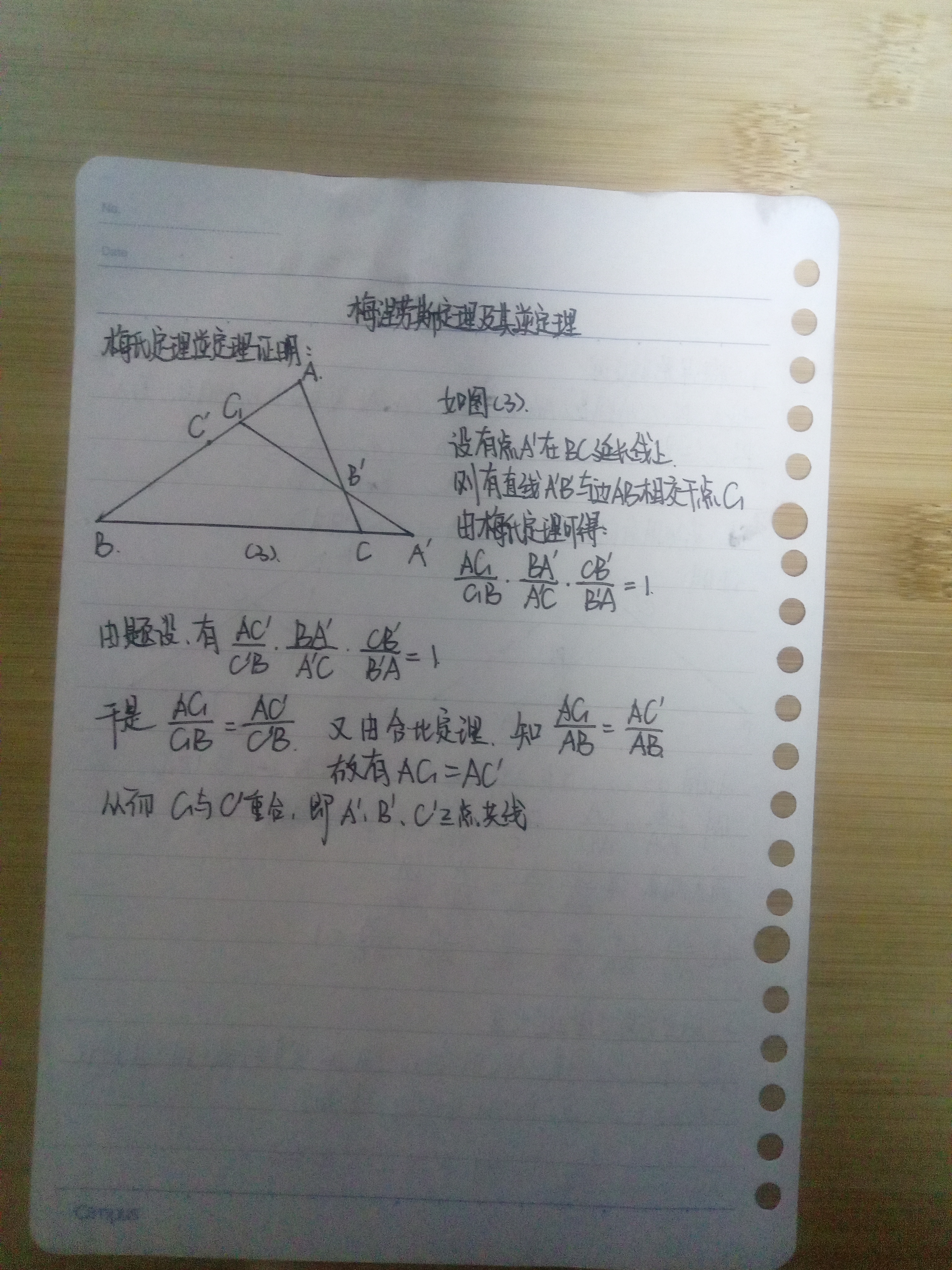
五、梅涅劳斯定理及其逆定理

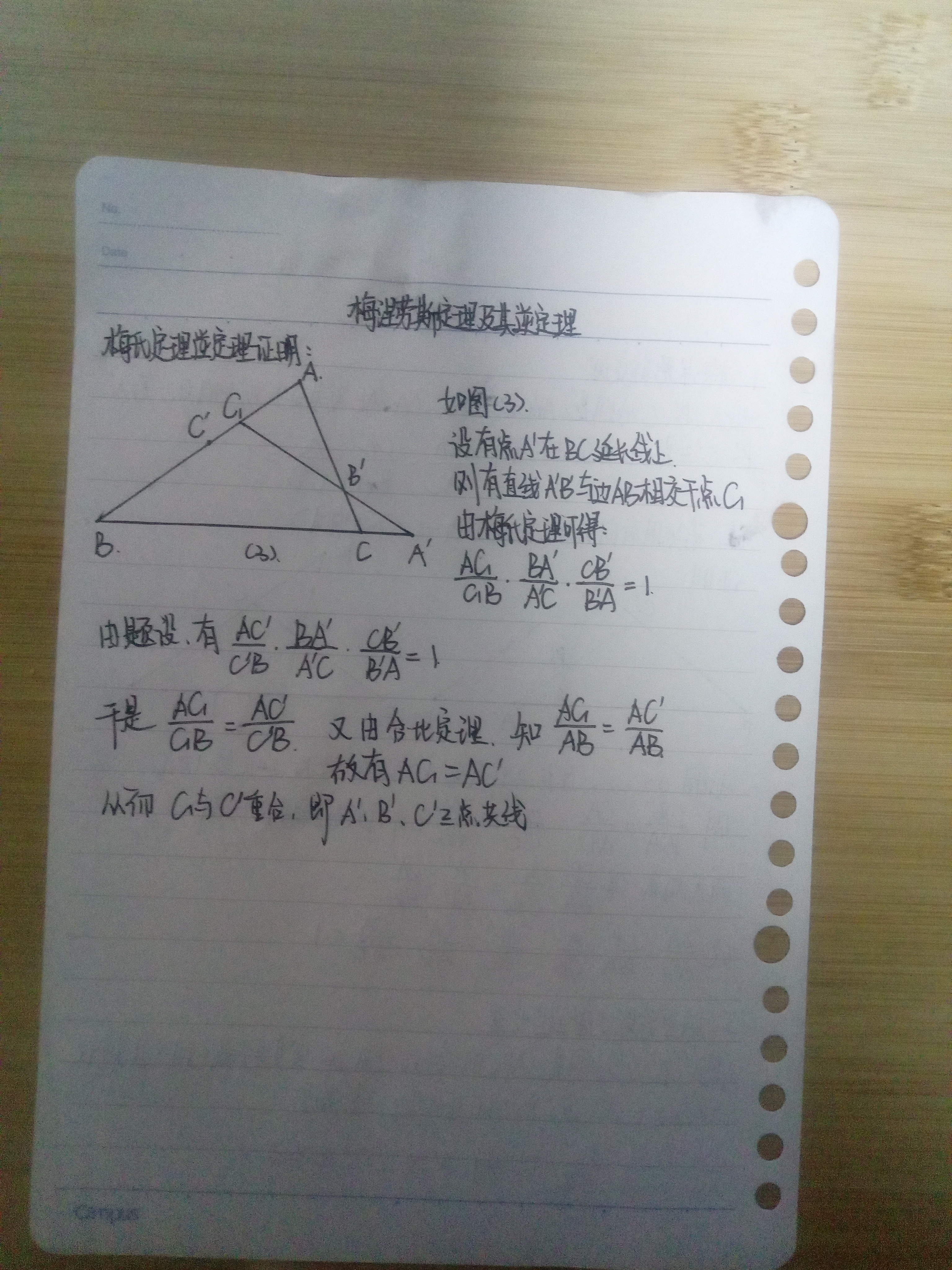
六、塞瓦定理及其逆定理

预备轮之几何跳转帖: