物理

[TINY NSD]为什么人民是历史的创造者？

零、引子

学过初中道法的人都知道，人民是历史的创造者

那么有没有人想过，这是为什么呢

作为一位数学爱好者，我决定用一个简单的数学模型加以说明

（以下模型作了大量的简化，不代表任何实际情形，特此声明）

首先，我们说明一下要作哪些简化：

①将人民简单分为两类：精英和平民

②忽略单身狗、再婚等一系列乱七八糟的情况

③每对夫妻恰好产生两个后代，分别视为父亲的子代和母亲的子代（这样人口数目就不会发生变化）

[模型1]假设第一代有五千万人，其中有五万分之一的精英；每个精英的子代有5%的概率是精英，每个平民的子代有99.99%的概率是平民，问：

（1）第n代有多少精英，多少平民？

（2）第n代中的精英，有多少的父辈是精英？

（3）经过足够长的时间后，可以近似认为一代中精英和平民的占比稳定，再求（1）（2）两问。

（4）假设由于某种原因，该地区两类人占比稳定之后，该代（成为新的第一代）有一半的平民死亡，再求（1）（2）（3）三问。

（5）通过以上内容，我们应该怎样提高精英的人数？

乍看起来，这是一种非常不公平的情形，平民的作用很有限，对吧？每个平民只有万分之一的概率逆天改命，而精英的子代成才率却要高500倍。真的是这样的吗？

对于这样的过程，我们发现，子代成才的情况仅仅依赖于ta的上一代，而与其他因素无关。这样的过程称为Markov过程。

当然，这里只把人分成两种类型，所以用高中课内的方法，求数列通项公式就可以解决问题了

但是，为了给接下来分析更复杂的Markov模型打基础，从这里开始，我们就要采用另一种方法了

什么方法？我们一起喊出它的名字：

线！性！！代！！！数！！！！

一、线性代数基础

一般讲线性代数会从行列式讲起，但出于应用的需要，这里先讲矩阵，行列式放到后面

矩阵的概念很简单，一个${m \times n}$的矩阵就是一张${m \times n}$的数表

如果${m=1，那么又称为行向量；如果n=1，那么又称为列向量}$

（是的就是高中讲的那个向量）

${n \times n}$的矩阵又叫${n阶方阵}$

下面，我们需要定义矩阵的运算：

①两个${m \times n}$的矩阵能进行加法运算，运算规则为：

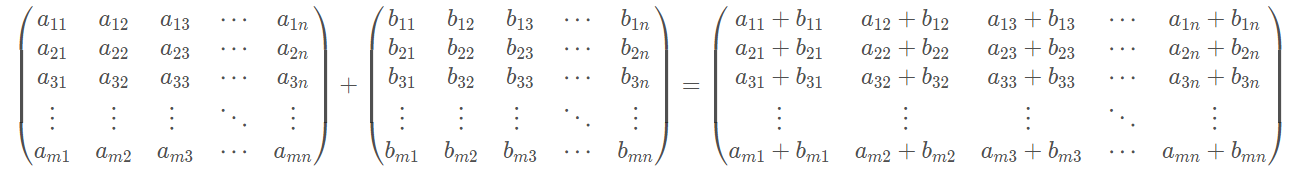
这很好理解，对吧

②任意一个矩阵与一个实数可进行数乘运算，运算规则为：

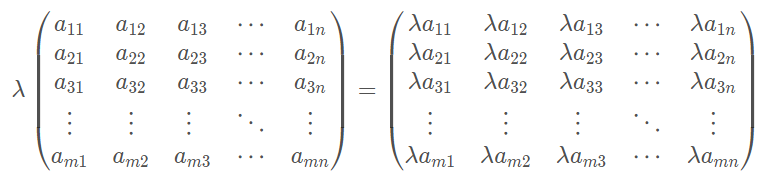
这也很好理解，对吧

③${m \times s 的矩阵和s\times n}$的矩阵可进行矩阵乘法运算，运算规则为：

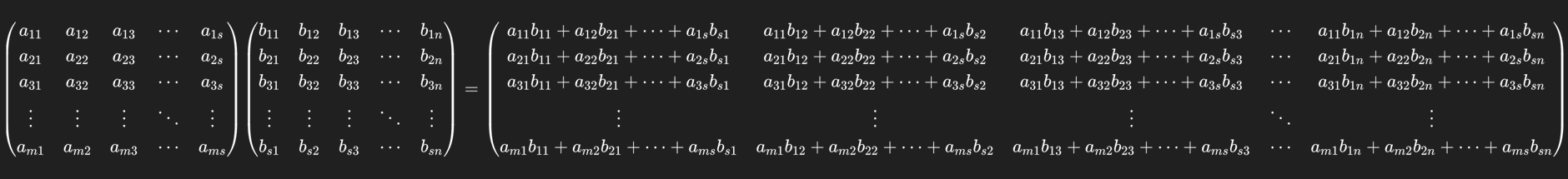
什么？太乱了？看不清？好，以下是慢一点的：

可是这怎么记？别着急，让我们观察一下这个式子

我们回顾一下高中所学向量的知识（散落在必修二第六章，选必一第一章和选必三第八章）

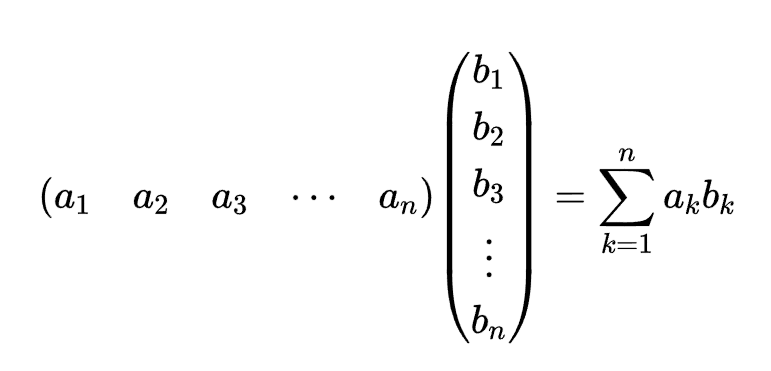
${(a_1, a_2, …, a_n) \cdot (b_1, b_2,…,b_n)=a_1b_1+a_2b_2+…+a_nb_n}$

实际上，在线性代数中，我们一般把它分别写成行向量和列向量：

然后我们又发现，矩阵其实可以写成很多个向量并排的形式，例如：

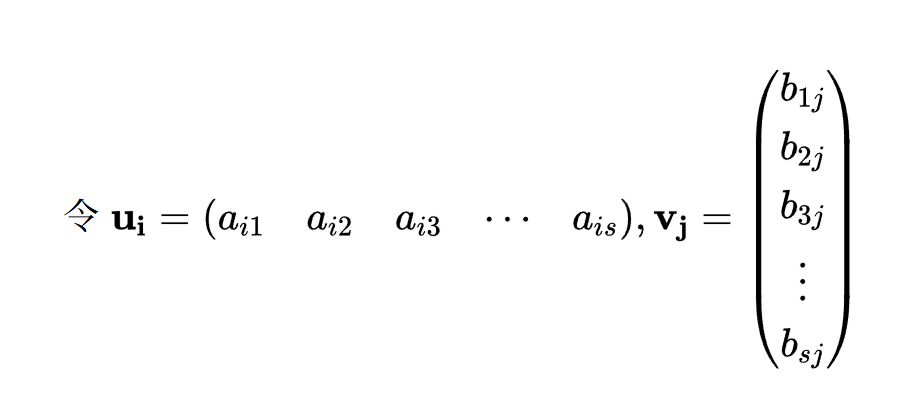
然后我们会惊喜地看到：

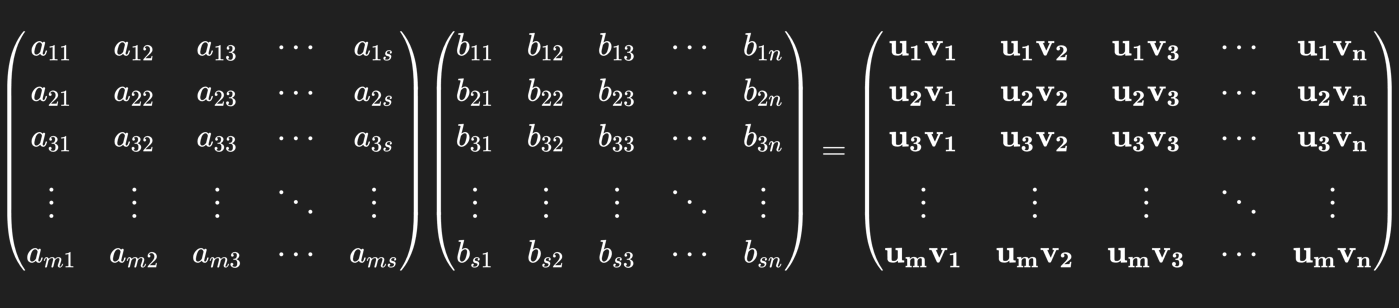
即${c_{ij}=\mathbf{u_iv_j}}$

这样是不是就很好理解了？

显然，矩阵乘法不满足交换律（因为交换完甚至可能无法运算），但我们惊奇地发现，矩阵乘法满足结合律！

（这里就不证明了）

在不久后我们就会发现，矩阵乘法的结合律会对简化运算起到很大的作用

④方阵的逆

在数的运算中，乘法的逆运算是除法，我们引入了倒数的概念，那么对于矩阵，是否存在这样的概念呢？

实际上，这一概念仅仅对n阶方阵存在

我们首先给出单位矩阵的定义：

对于${n阶方阵A，若存在n阶方阵B使AB=BA=I_n，则称B为A的逆矩阵，记作A^{-1}=B}$。

那我们该如何判断逆矩阵是否存在？又该如何计算逆矩阵？

接下来，我们就要引入行列式（记为${\det A}$）和代数余子式的概念了

（实际上行列式不是这么定义的，但为了方便讲述，从递推的角度入手）

若1阶方阵${A=(a)，则\det A=a}$

对于n阶行列式，称元素${a_{ij}的余子式M_{ij}为矩阵划去第i行和第j列后，剩下的(n-1)阶方阵的行列式}$

${并称代数余子式A_{ij}=(-1)^{i+j}M_{ij}}$

定义${\det A_{n \times n}=\sum_{j=1}^n{a_{ij}A_{ij}}=\sum_{i=1}^n{a_{ij}A_{ij}}}$

（只要在一次计算时保持一致，第一个式子里的i和第二个式子里的j是可以任取的！就是这么神奇！）

这样就把n阶行列式拆成了若干(n-1)阶行列式加权后的和，归纳即可求出

可以证明，矩阵A可逆（即逆矩阵存在）当且仅当其行列式不为0。

那么，我们该如何具体求出逆矩阵呢？

我们定义A的伴随矩阵${A^*}$：

注意：A中某一行的代数余子式出现在${A^*}$中对应的列！

可以证明：${AA^*=A^*A=\det A \cdot I_n}$

（注意：一般来讲交换律是不成立的，但是相乘为单位矩阵的常数倍时可以交换！）

于是我们可以写出：${A^{-1}=\frac{1}{\det A} A^*}$

这就是逆矩阵的求法。

接下来，我们需要研究矩阵的乘方：

（翻回乘法公式看一眼，问：有人愿意一个一个乘起来吗？好，没有，我们继续）

首先，我们需要定义对角矩阵的概念：

若${\forall i \ne j,a_{ij}=0，则称A为对角矩阵}$，

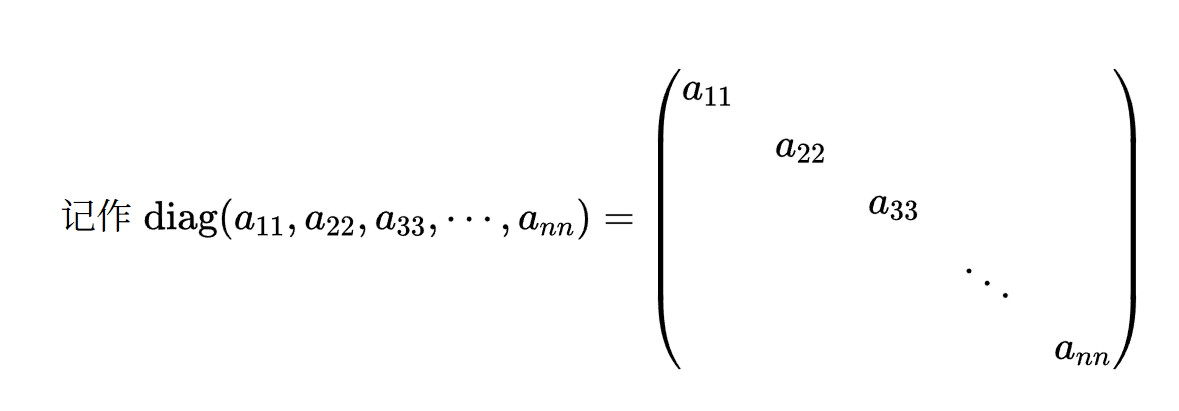
很容易发现，${\operatorname{diag} (a_{11}, a_{22},a_{33}, \cdots, a_{nn}) \operatorname{diag} (b_{11}, b_{22}, b_{33}, \cdots,b_{nn})=\operatorname{diag} (a_{11}b_{11}, a_{22}b_{22}, a_{33}b_{33}, \cdots,a_{nn}b_{nn})}$。

所以，我们试图把一般的方阵转化为对角矩阵

我们发现，如果对于n阶方阵A，存在n阶可逆方阵P使${A=PDP^{-1}（D为对角矩阵）}$，那么由结合律，A的乘方会大大简化

但这样的方阵是否存在？该如何找到？这时，我们需要引入两个新的概念：

${若存在数\lambda和n维列向量\mathbf{v}满足A\mathbf{v}=\lambda \mathbf{v}，则称\lambda为A的特征值，\mathbf{v}为A的特征向量}$

（值得注意的是，“特征向量”的英文为eigenvector，这就是“即未”英文名的出处）

同时还要定义向量之间的一种关系：

若行列式${\det (\mathbf{v_1~v_2~v_3~\cdots~v_n}) \ne 0,则称\mathbf{v_1,v_2, \cdots, v_n}线性无关}$。

可以证明，n阶方阵A可对角化当且仅当其存在n个线性无关的特征向量。

且${D=\operatorname{diag} (\lambda_1, \lambda_2, \cdots, \lambda_n)}$，${P=(\mathbf{v_1~v_2~\cdots~v_n})}$，

其中${A\mathbf{v_i}=\lambda_i\mathbf{v_i}}$

而很显然，只需要知道特征值，就可以推出特征向量。于是我们的问题转化为：如何求特征值？

事实上，${A\mathbf{v}=\lambda\mathbf{v}当且仅当\det (A-\lambda I_n)=0}$

所以问题最终就转化为了一个多项式方程，只要解出方程，就可以得到结果

而由${A=PDP^{-1}和乘法结合律，即有A^n=PD^nP^{-1}，D^n可以利用对角矩阵的乘法简化计算}$。

这样，我们定义了矩阵的各种运算和计算方法，而这也正是我们接下来的内容所需要的基础知识。

二、双状态Markov过程的一般分析思路

我们先用p和q表示${精英\rightarrow精英和平民\rightarrow平民的概率}$，再代入模型1中的数据。

（为方便讨论，考虑p，q不同时为0，也不同时为1）

很显然，这个Markov过程有两个状态：精英和平民。

我们定义Markov过程的转移矩阵：第i行第j列为由状态j转移到状态i的概率

这样，我们可以写出这个Markov过程的转移矩阵：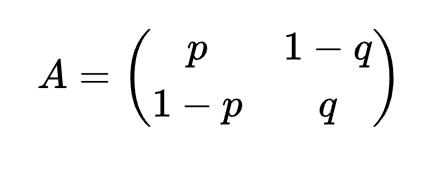

同时，我们可以把第n次转移过后各状态的概率写成列向量的形式：

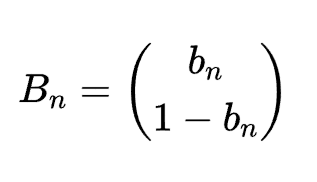
不难发现，${B_{n+1}=AB_n，从而B_n=A^nB_0}$

问题很简单：${A^n}$怎么求？

对角化！

设${\det (A-\lambda I_2)=0}$，则${(p-\lambda)(q-\lambda)=(1-p)(1-q)}$

解得${\lambda=1或p+q-1}$

(由这一个结果，可以说明无论${p，q取何值，二阶Markov转}$移矩阵均可对角化，不多说明)

当${p=q=1时，A=I_2，后面的问题也就差不多那样了}$

否则，由这两个特征值，再利用定义特征值和特征向量的方程，可以解出两个特征向量：

${\mathbf{v_1}=\begin{pmatrix}1-q\\1-p\end{pmatrix}}$

${\mathbf{v_2}=\begin{pmatrix}1\\-1\end{pmatrix}}$

于是可以令${D=\operatorname{diag} (1, p+q-1)}$,

完成对角化仅差最后一步：硬算${P^{-1}，然后把A^n=PD^nP^{-1}}$给算出来

开始！

${\det P=-(1-q)-(1-p)=p+q-2，}$

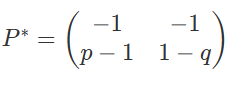
从而：

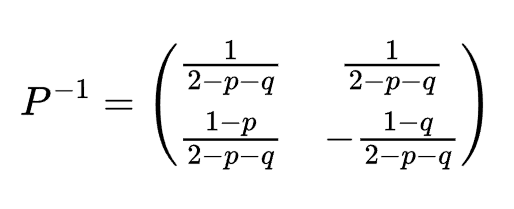
后面的计算我就不一一写了，太占篇幅，最后结果：

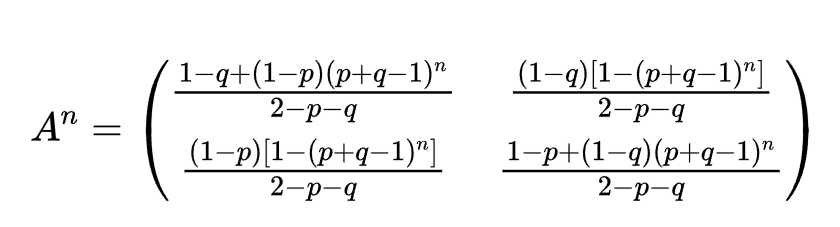
我们离求出${B_n}$只有一步之遥了

${B_n=A^nB_0}$

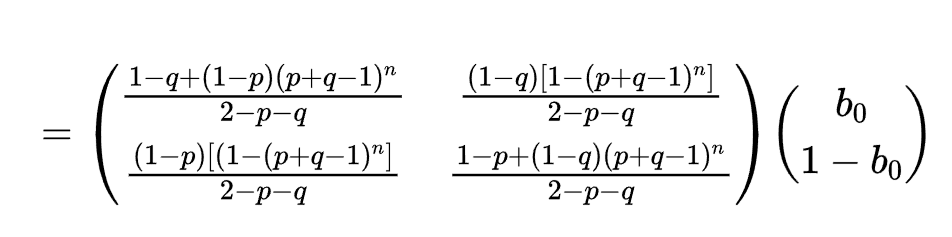
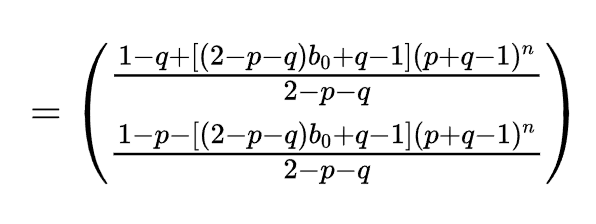
即${b_n=\frac{1-q+[(2-p-q)b_0+q-1](p+q-1)^n}{2-p-q}}$

三、对模型1的解答

根据模型1，${p=0.05,q=0.9999, b_0=0.00002}$

代入得${b_n=\frac{1-0.80998 \times0.0499^n}{9501}}$

在这个模型下，人口总数是不变的，所以第n代的精英人数即为${5 \times 10^7 b_n}$

而平民人数即为${5 \times 10^7 (1-b_n)}$

对于（2），很明显需要利用贝叶斯公式：

${r_n=\frac{b_{n-1}p}{b_{n-1}p+(1-b_{n-1})(1-q)}=\frac{500-404.99\times 0.0499^{n-1}}{10000-404.18002 \times 0.0499^{n-1}}}$

同样，不再详细计算，（1）（2）的结果列一个表：

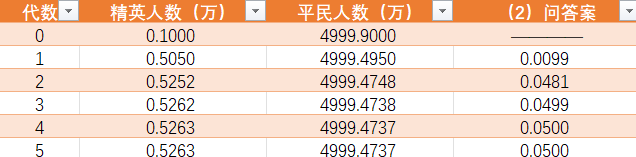
其实这相当于同时把（3）给解答了，但是这显然不是我们的目的

由于我们假设${p, q}$不同时为0或1，总有${\lim_{n \rightarrow \infty}(p+q-1)^n=0}$，

从而${\lim_{n \rightarrow\infty}b_n=\frac{1-q}{2-p-q}}$，${\lim_{n \rightarrow\infty}(1-b_n)=\frac{1-p}{2-p-q}}$

故${\lim_{n \rightarrow\infty}r_n=\frac{p(1-q)}{(1-p)(1-q)+p(1-q)}=p}$

式子极其简洁，但说明了一件事：在足够长时间后，父代是精英的精英占比，总是等于子代是精英的精英占比

后者不可能取到一个很大的值（在实际情况下，p绝对不可能高达0.05）

故绝大部分的精英，其父代都是平民

同时我们再观察上面的表格，在精英很少的时候，${r_n}$的值高于稳定值

也就是说，在发展的过程中，每一代的几乎所有精英，其父代都是平民

关于（4），求解方法类似，不作详细解释

很容易发现，稳定后，精英和平民的占比不变，但是由于人口数只减不增，意味着精英的人数也减少了接近一半（不到一半，实际上是${\frac{4750}{9501}}$）

这说明，平民人数的减少，在这样的模型下也会对精英造成极大损害

对于（5），我们考虑一个问题：为使最终的精英人数变为现有的2倍，在人口数不变的情况下，应该重点提升精英的成才率还是平民的成才率？

考虑其中一个值不变的情况：

若${q=0.9999}$不变，则${\frac{1-0.9999}{2-0.9999-p}=\frac{2}{9501}}$

解得${p=0.52505}$，相当于将精英的成才率提高到10倍还多

若${p=0.05}$不变，则${\frac{1-0.05}{2-0.05-q}=1-\frac{2}{9501}

解得${q \approx 0.99979998}$，${1-q \approx 0.00020002}$

即只需要将平民的成才率提高到2倍略多一点

这说明，重视基础教育，让平民有更多逆天改命的机会，对于社会的发展是合理的