物理

信息竞赛中的一些算法：并查集、最小生成树和打表

这是一个关于信息竞赛的帖子。

$A\to B$ 表示把 $A$ 的值设为 $B$。

$a[i]$ 表示数组 $a$ 的第 $i$ 项。

$i$ 除非特殊说明，不指虚数单位。

某些词语可能使用不规范，请大家指出。

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$

王大爷说：我的孙子学了什么信息竞赛的什么树之后就说什么要删去祖先，要是他真的把我“删了”怎么办！

从事剪枝工作的李师傅说：我儿子经常说要“剪枝”，随便破坏树木不好啊！他也不知道这项工作有多难，收入也低！

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

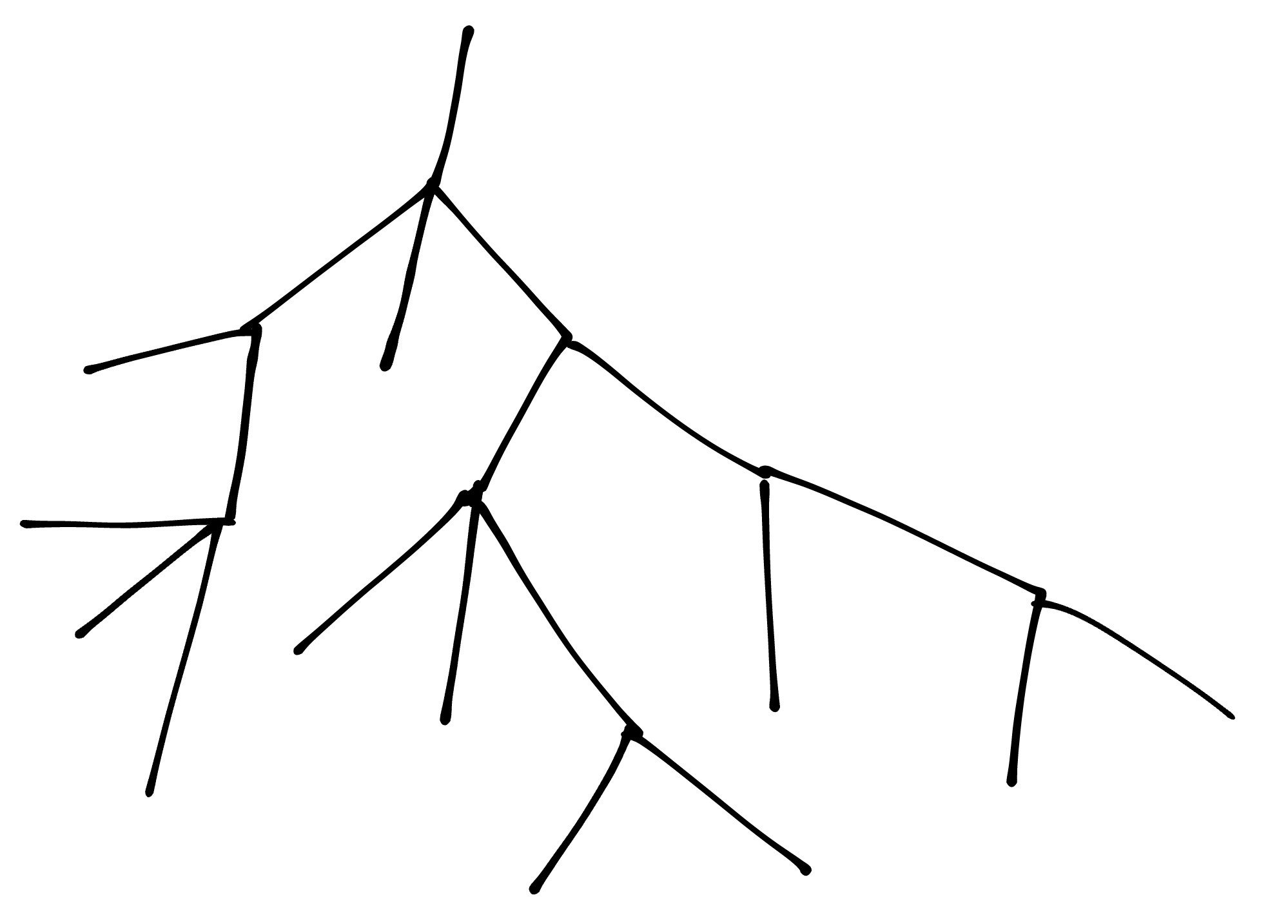
先来理解什么是“树”。

一个节点是树，称这个节点是树的根节点。

一个节点①与几个树的根节点②连接的东西也是树，其中①是这整个树的根节点，①也是②的父端点。

像下面的图片就是一棵树。

[图一]

$\Huge{\text{一：并查集}}$

如果我们有一些元素：$a_1,a_2,\dots,a_n$，它们属于不同的集合。

我们可以进行一些操作，如下：

并 x y：把 $x$ 所在的集合与 $y$ 所在的集合合并。

查 x y：如果 $x$ 和 $y$ 在同一个集合里，输出 $1$，否则输出 $0$。

让我们先创建数组 $p_1=1,p_2=2,\dots,p_n=n$

$p_n$ 表示第 $n$ 个节点的父节点（一个节点可能有多个子节点，但只能有一个父节点）。

我们需要让相同的集合在同一棵树上。

如果“查”，就判断两个集合所在树的根节点是否相同。

如果“并”，就把一个集合所在树的根节点的父节点设为另一个集合所在树的根节点。

$\Huge{\text{二：最小生成树}}$

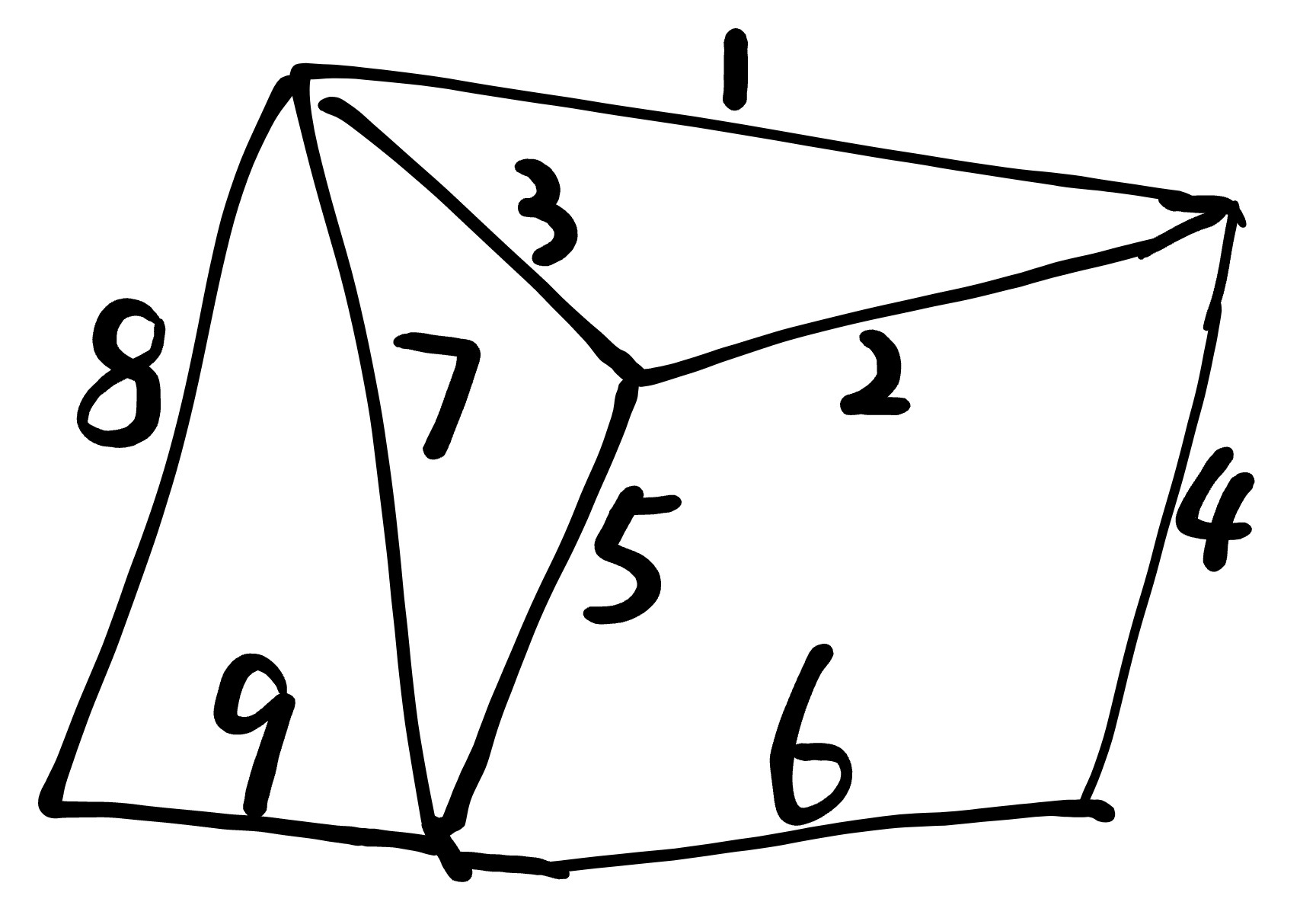
这是一个图：

[图二]

我们要画一棵树，连接它的所有端点。

要求树每一边的数之和最小。

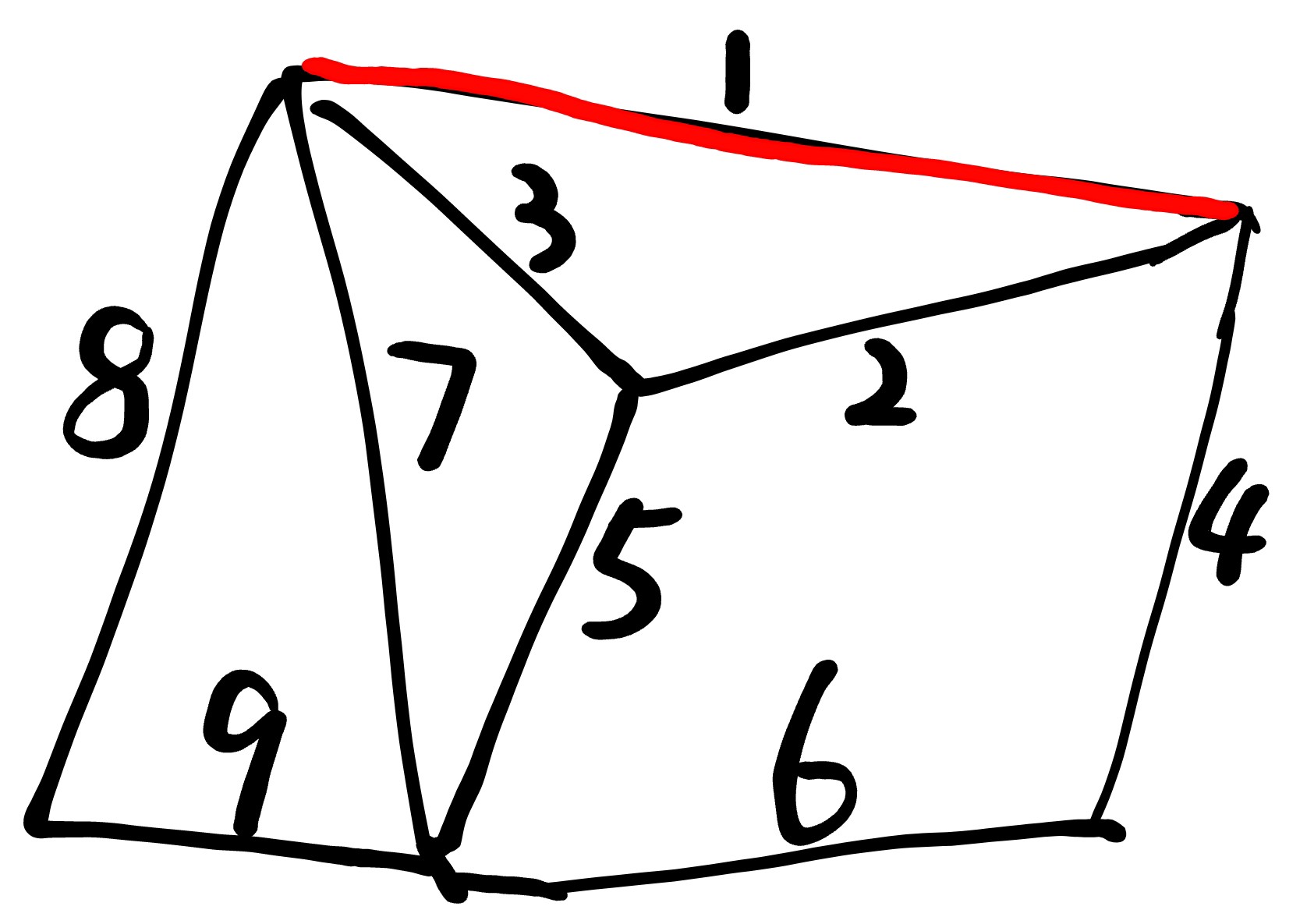
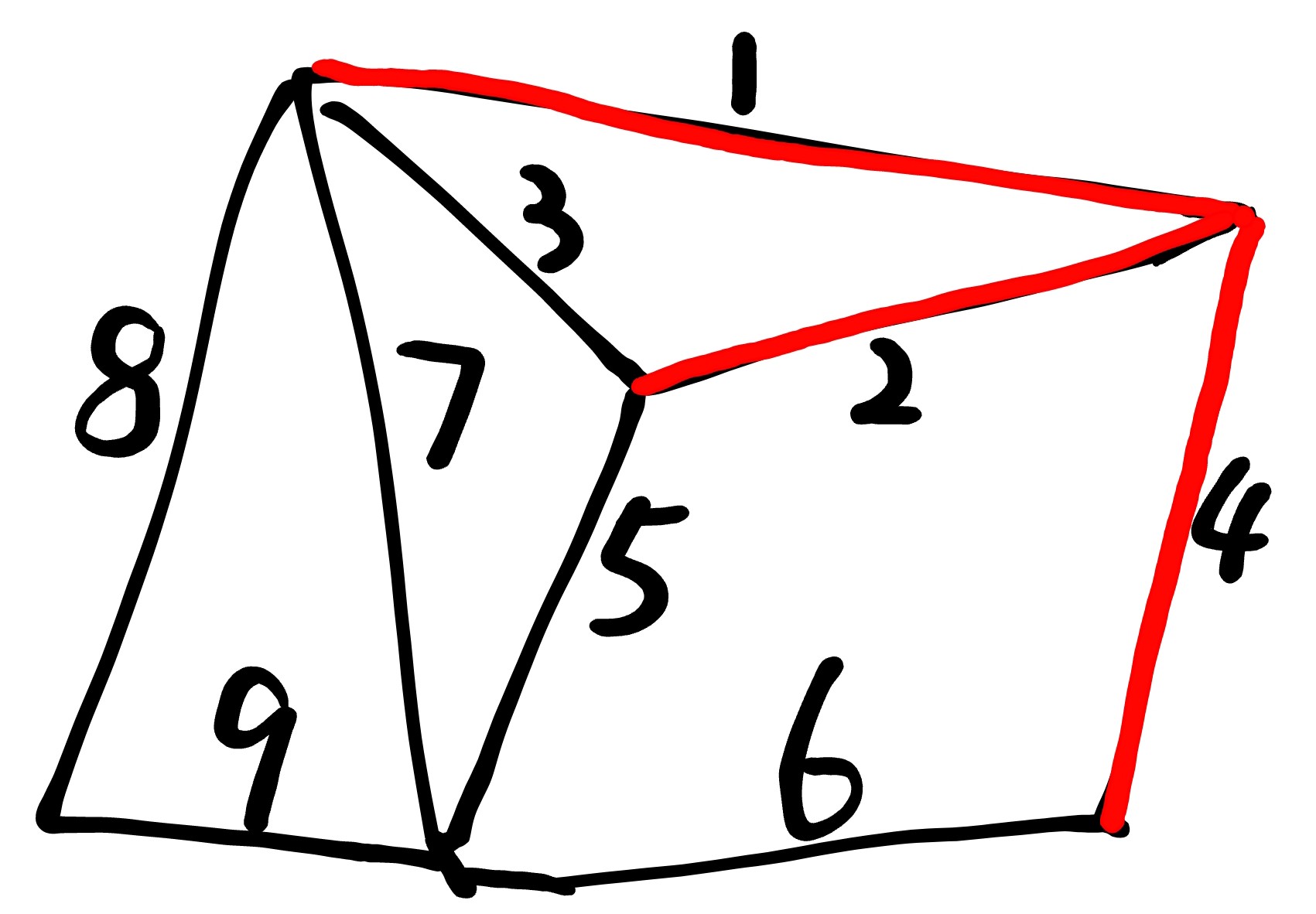
于是根据贪心算法，我们找到最小的边：（1）

[图三]

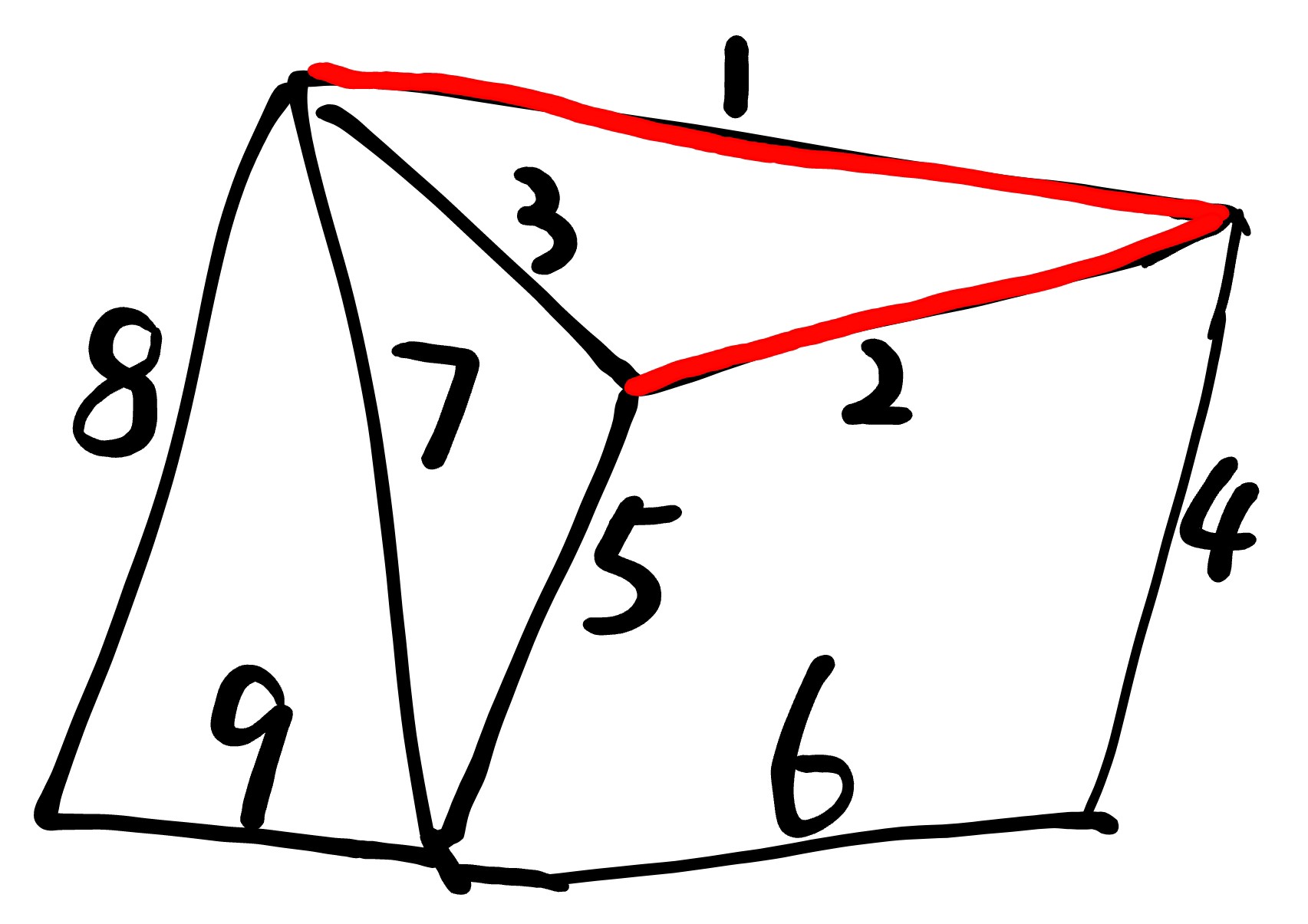
找剩下的边中最小的边：（2）

[图四]

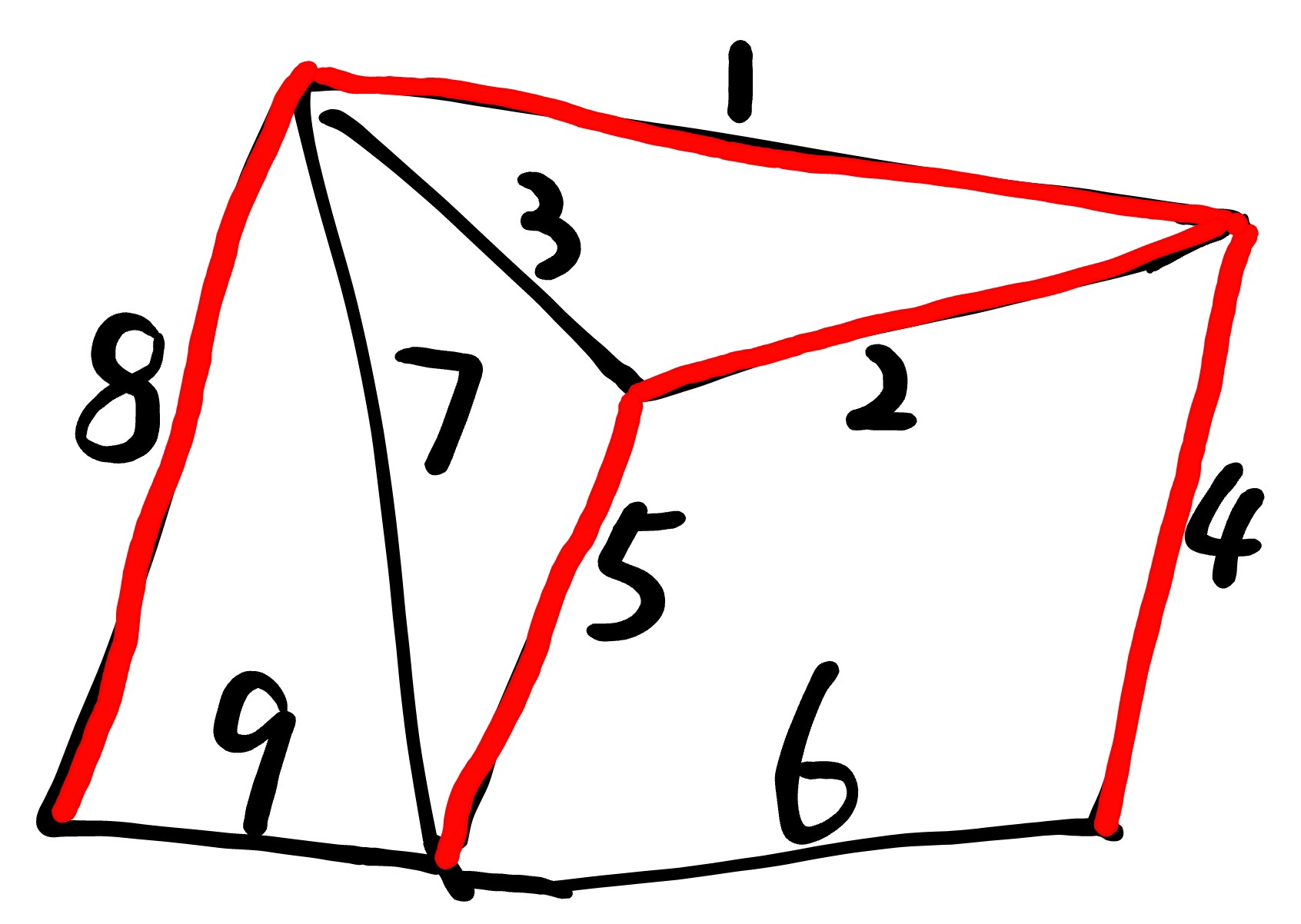
找到剩下边中最小的边：（3）

等等！你可能发现了，选这条边后，组成的图形就不是一个树了，于是找到次小边。（4）

[图五]

重复过程，直到连接所有端点。

[图六]

像这样就可以了。

那么，如何判断连接某一条边后，组成的图形是不是树呢？

只需要判断这条边的两个端点是否在同一棵树上就可以了。

$\Huge{\text{三：打表}}$

题目：输入 $n$，计算 $1!+2!+\dots+n!$，$1\lt n\le50$。

注意只有 $50$ 种输入，手动计算出对应输出就可以了。