物理

使用神经网络和梯度下降算法拟合函数过程与原理（1）：神经网络的计算过程和训练过程

这篇帖子的内容与数学有关。

提示：难度约等于基础轮，大家可以放心食用。

（上次发帖讲了插值，这次讲拟合）

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$

$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$

神经网络是一项古老的技术，它出现在动物出现大脑和神经元时。

如今，很多人工智能的原理都涉及到神经网络。

[图一]

关于公式的一些约定：

下标从 $1$ 开始。（OIer 们，对不起，我是故意的）

$A\to B$ 表示把 $A$ 的值设为 $B$。

函数名称可能有多个字符，如表示乘法，会加上 $\cdot$。

神经网络看起来复杂，但它就是一个（复杂的）函数：

$N_\theta(x)$

其中，$\theta$ 表示参数向量，$N_\theta(x)$ 表示参数为 $\theta$ 时，$N(x)$ 的值。

当然 $x$ 不是一个数，它是一个向量。

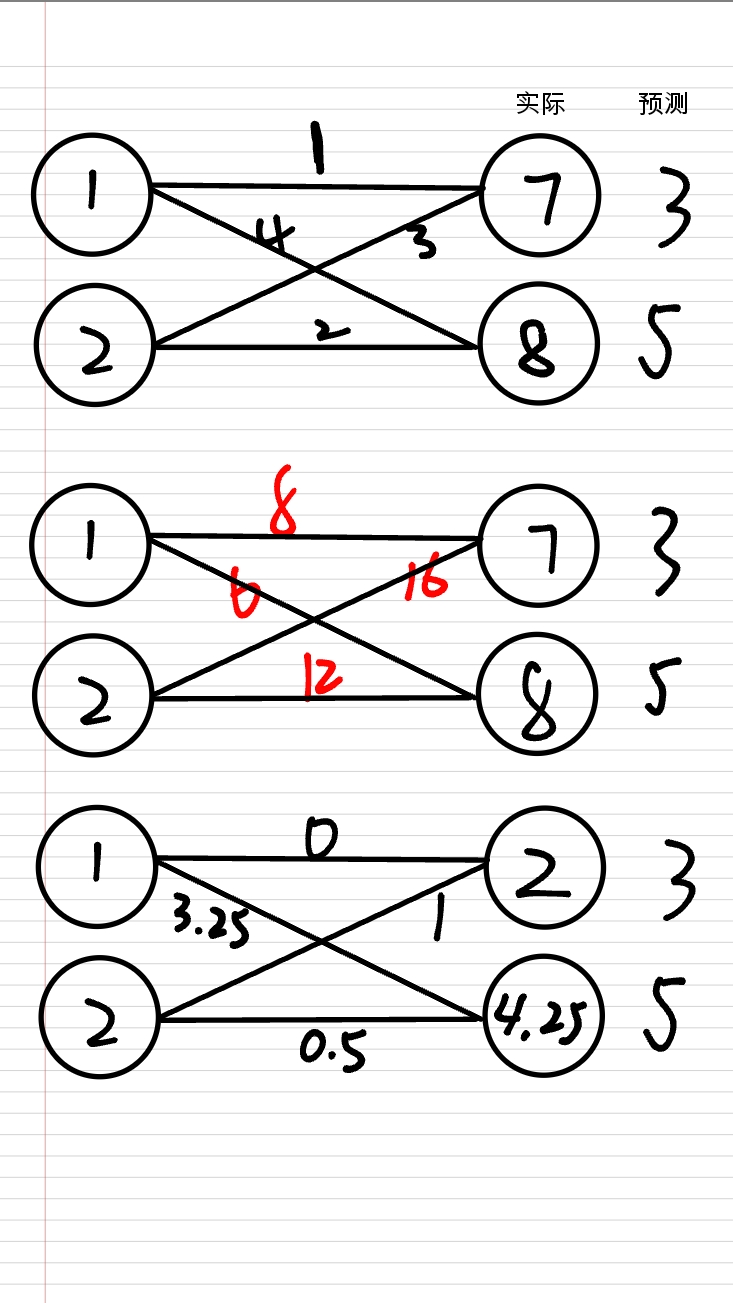
神经网络分为很多层，每一层有很多神经元，每一个神经元根据上一层神经元的信息计算并得到结果。

每一层是这样计算的：

$N_{i+1}=\sigma(W_iN_i+b_i)$

其中 $N_i$ 表示第 $i$ 层的神经元信息，$W_i$ 表示（这一层的）权重矩阵，$b_i$ 表示（这一层的）偏置向量。

显然，前文中的 $\theta$ 这个向量是把所有权重矩阵（使用一向箔）降维，与偏置向量连接，再排列成向量的结果。

$\sigma$ 是激活函数，这里指对运算结果逐元素操作。它有很多种。

神经网络分为多层，分为三类：

输入层，接受输入的数据并转为向量形式。

隐藏层，对输入层的数据进行运算。

输出层，接受运算完成的数据。

激活函数

激活函数分为很多种，这里举出几种例子：

$\large{\text{ReLU}}$

ReLU 非常简单，它是这样的：

$\operatorname{ReLU}(x)=\begin{cases}x&x\ge0\\0&x\lt0\end{cases}$

它的导数：

$\operatorname{ReLU}'(x)=\begin{cases}1&x\ge0\\0&x\lt0\end{cases}$

显然它计算非常快，仅需一次比较。

$\large{\text{Leaky ReLU}}$

$\operatorname{ReLU}(x)=\begin{cases}x&x\ge0\\ax&x\lt0\end{cases}$

其中 $1\gg a\gt0$，$a$ 是一个小正数，如 $0.01$。

导数：

$\operatorname{ReLU}'(x)=\begin{cases}1&x\ge0\\a&x\lt0\end{cases}$

$\large{\text{Sigmoid}}$

$\operatorname{sigmoid}(x)=\frac{1}{1+e^{-x}}$

Sigmoid 是一个典型的 S 形曲线。

$\lim\limits_{x\to-\infty}\operatorname{sigmoid}(x)=0$ 和 $\lim\limits_{x\to\infty}\operatorname{sigmoid}(x)=1$ 说明它可以被用在输出层，如下：

假设你训练一张神经网络，输出是你输入的一句话正确的概率。

但是神经网络的输出没有限制，从负无穷到正无穷都有可能。（当然其实还是有一个很大的范围）

于是你考虑在输出层增加 Sigmoid 函数，把输出压缩到 $0$ 和 $1$ 之间。再乘以 $100\%$，就能得到概率。

Sigmoid 的导数计算留给读者。

$\large{\text{Swish}}$

某公司使用 Swish 训练神经网络，他们评价“非常好用”。

$\operatorname{Swish}(x)=\frac{x}{1+e^{-x}}$

可以看出 Swish 就是 Sigmoid 的变体。

$\large{\text{Softmax}}$

$\operatorname{Softmax}(x_i)=\frac{e^{x_i}}{e^{x_1}+e^{x_2}+\dots+e^{x_n}}$

一个简单的归一化函数，用于计算多分类问题的概率。放在输出层。

现在，你已经大致了解了一次神经网络计算的过程：

第一步：把输入层的数据设为输入内容。

第二步：依次计算隐藏层。

第三步：输出输出层的内容。

下一步是训练神经网络。

训练神经网络需要一种优化算法，本帖中使用梯度下降作为示例。

梯度下降可以概括成一个公式：

$\theta\to\theta-\alpha\cdot\nabla$

其中 $\theta$ 是参数，$\alpha$ 是学习率。

那个倒过来的三角形是什么？它是梯度，就是偏导数的向量。这里指损失函数对每一个参数的导数。

损失函数可以衡量输出结果与预测结果（你需要的结果）的符合程度。

这里设 $r_i$ 表示实际的第 $i$ 个输出，设 $x_i$ 表示预测的第 $i$ 个输出（就是你希望得到的输出）。

（其中一种）（最基础的）损失函数 $\operatorname{loss}(r)=\frac12(\sum_{i=1}^{n}(x_i-r_i)^2)$。

损失函数越小，表示实际和预测越接近。

优化算法用来解决一类问题，例如：

已知 $f(x)=e^x-2x$，求它什么时候取到最小值。

你可以选择直接求导，得到方程 $f'(x)=e^x-2=0$。

但是对于神经网络这一个（坨）复杂的函数，还要套上一个损失函数，你很难解这个有几亿个未知数的方程组。甚至你无法求出它的导数的解析式。

因为无法求出解析解，我们要想办法求出数值。

例如 $f'(x)\approx\frac{f(x+\Delta)-f(x-\Delta)}{2\Delta}$。

这样每计算一个偏导数，要算两次 $f$ 函数，比较慢。

所以，我们可以使用一种全新的方法：自动微分。

大家都知道，$\frac{\mathrm{d}}{\mathrm{d}x}f(g(x))=f'(g(x))\cdot g'(x)$，我们可以轻松的把它推广到偏导数。

自动微分就是这么计算的。

比如算 $\frac{\mathrm{d}}{\mathrm{d}x}f(g(n))$（$n$ 已知），假设 $f$ 和 $g$ 都是非常简单的函数，但把它们合起来你就不会了。这时，你可以使用自动微分：

先算出 $g(0)$，

然后算出 $\frac{\mathrm{d}}{\mathrm{d}g(x)}f(g(n))=f'(g(n))$，

然后算出 $g'(0)$，

然后得到 $\frac{\mathrm{d}}{\mathrm{d}x}f(g(n))$ 和 $f(g(n))$。

如果函数复杂一些，例如 $\frac{\mathrm{d}}{\mathrm{d}x}f(h(k(n)))$，这时可以使用下面的方法：

设 $g(x)=h(k(x))$，

然后用上面的方法算出 $g(0)$ 和 $g'(n)$，

使用上面的方法算出 $\frac{\mathrm{d}}{\mathrm{d}x}f(g(n))$ 和 $f(g(n))$，

代回原式，得到 $\frac{\mathrm{d}}{\mathrm{d}x}f(h(k(n)))$ 和 $f(h(k(n)))$。

然后我们仿照上面的方式，选择一组训练数据 $i$，对于每个 $j$ 计算出 $\frac{\mathrm{\operatorname{loss}(N_\theta(x))}}{\mathrm{d}\theta_j}$。

然后把它们组成向量 $\nabla_i$。

计算完所有训练数据后，计算平均梯度 $\nabla_{avg}=\sum_i\nabla_i$。

最后把 $\theta$ 改为 $\theta-\alpha\cdot\nabla$。

重复以上过程，损失函数的值会越来越低，等到它足够低了，就说明训练完成了。

（使用神经网络和梯度下降算法拟合函数过程与原理（1）完）