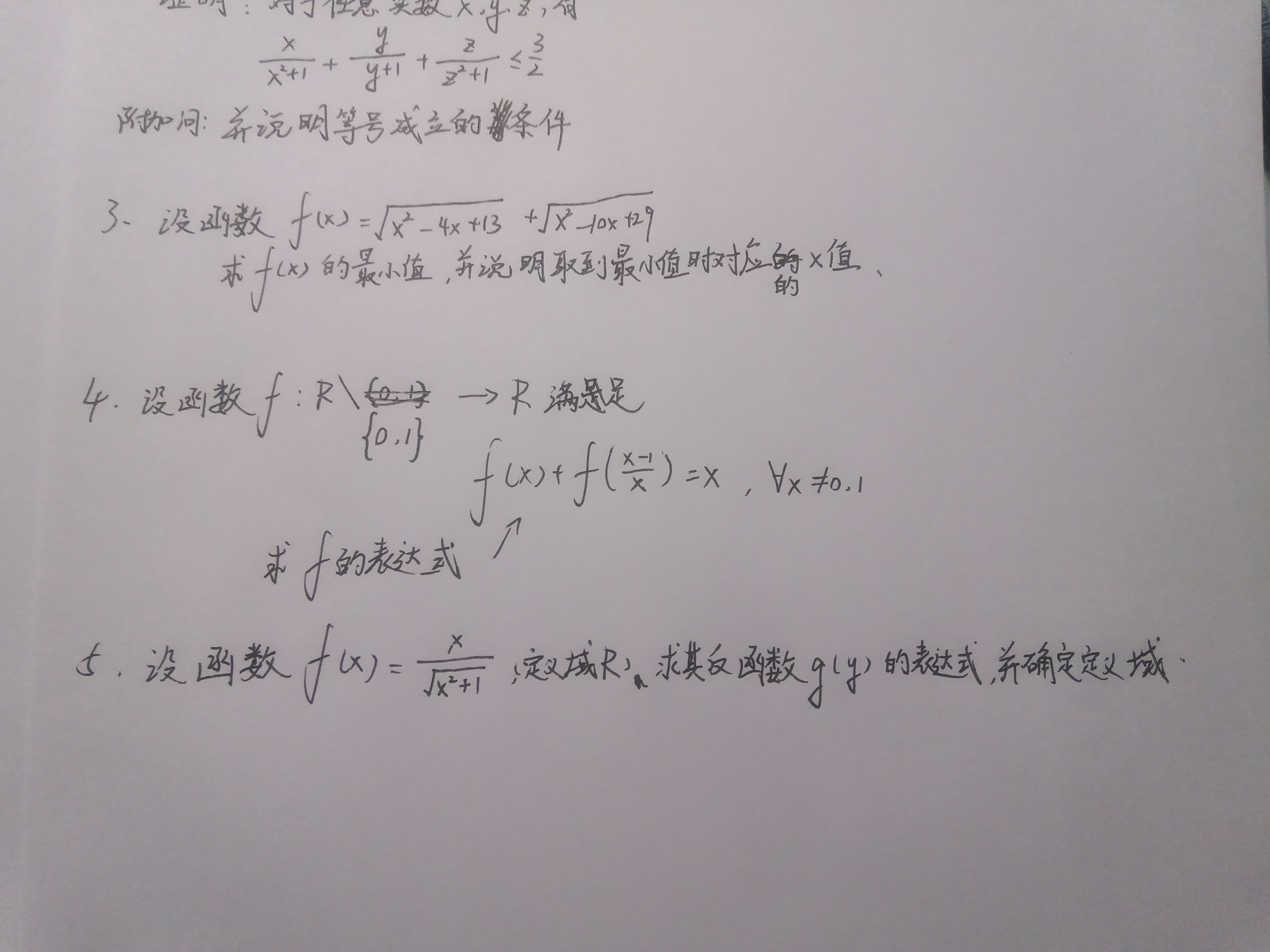- 1
没学过数竞，做一下第一题(
求导消$f(y)$项：
$$f'(x+y)=f'(x)+6xy+3y^2,\quad \forall y\in\mathbb{R}$$
$x=0$时得：
$$f'(y)=f'(0)+3y^2$$
$$f(y)=\int (f'(0)+3y^2)dy=y^3+f'(0)y+C$$
易证$f(0)=0$所以$C=0$。
所以
$$f(x)=y^3+ky,\quad \forall k\in\mathbb{R}$$
代入验证，对的。
⑵注意到对于$∀x∈R,x^2+1≥2x$，当且仅当$x=1$时取等,于是$\frac{x}{x^2+1}≤\frac{1}{2}$,同理有
$\frac{y}{y^2+1}≤\frac{1}{2}$,$\frac{z}{z^2+1}≤\frac{1}{2}$,三式相加即得题给不等式（好像那个分母的y是y^2?）
取等条件为$x=y=z=1$
⑶注意到，$f(x)=\sqrt{(x-2)^2+9}+\sqrt{(x-5)^2+4}=\sqrt{(x-2)^2+(0-3)^2}+\sqrt{(x-5)^2+(0-2)^2}$
考虑它的几何意义：平面上两定点$A(2,3)$,$B(5,2)$,在$x$轴上有一动点$P(x,0)$,即求$\left|PA\right|+\left|PB\right|$的最小值
（将军饮马）作一条过$(2,3)$和$(5,-2)$的直线，求得该直线方程为$5x+3y-19=0,\left|AB\right|=\sqrt{34}$,直线与$x$轴的交点即为取得最小值时点$P$的坐标,$x=\frac{19}{5}$，∴当$x=\frac{19}{5}$时，函数$f(x)$有最小值$\sqrt{34}$
⑷由条件，有：
$f(x)+f(\frac{x-1}{x})=x$ ......(i)
$f(\frac{x-1}{x})+f(\frac{1}{1-x})=\frac{x-1}{x}$ ......(ii)
$f(\frac{1}{1-x})+f(x)=\frac{1}{1-x}$ ......(iii)
（i）式与（iii）式相加，减去（ii）式，得到
$f(x)=\frac{x^3-2x^2+x-1}{2x^2-2x}$
2是对的，分母确实是y方(之前有人提过的但我貌似忘改了)，大佬容我mol(好像在直播上见过你？)
其他两题容我吃完饭回来看
24年的。？没看过呢，好像那会我还在上新手轮🤡
收下了，找个机会做做看(虽然99%会被拷打♿♿♿)
第十九题好像有意思🤧
这是我从其他佬的帖里截下来的，呃
是，但是学的不太精哈😖不要把我当大佬看，我还被物理电学折磨呢😩
最近差不多淡坛了，好好学竞赛轮了😤
坛上的大佬比我厉害不知道多少倍😭
只能说早培怪恐怖如斯
这起步时间都够我学两遍了 怎么玩k
