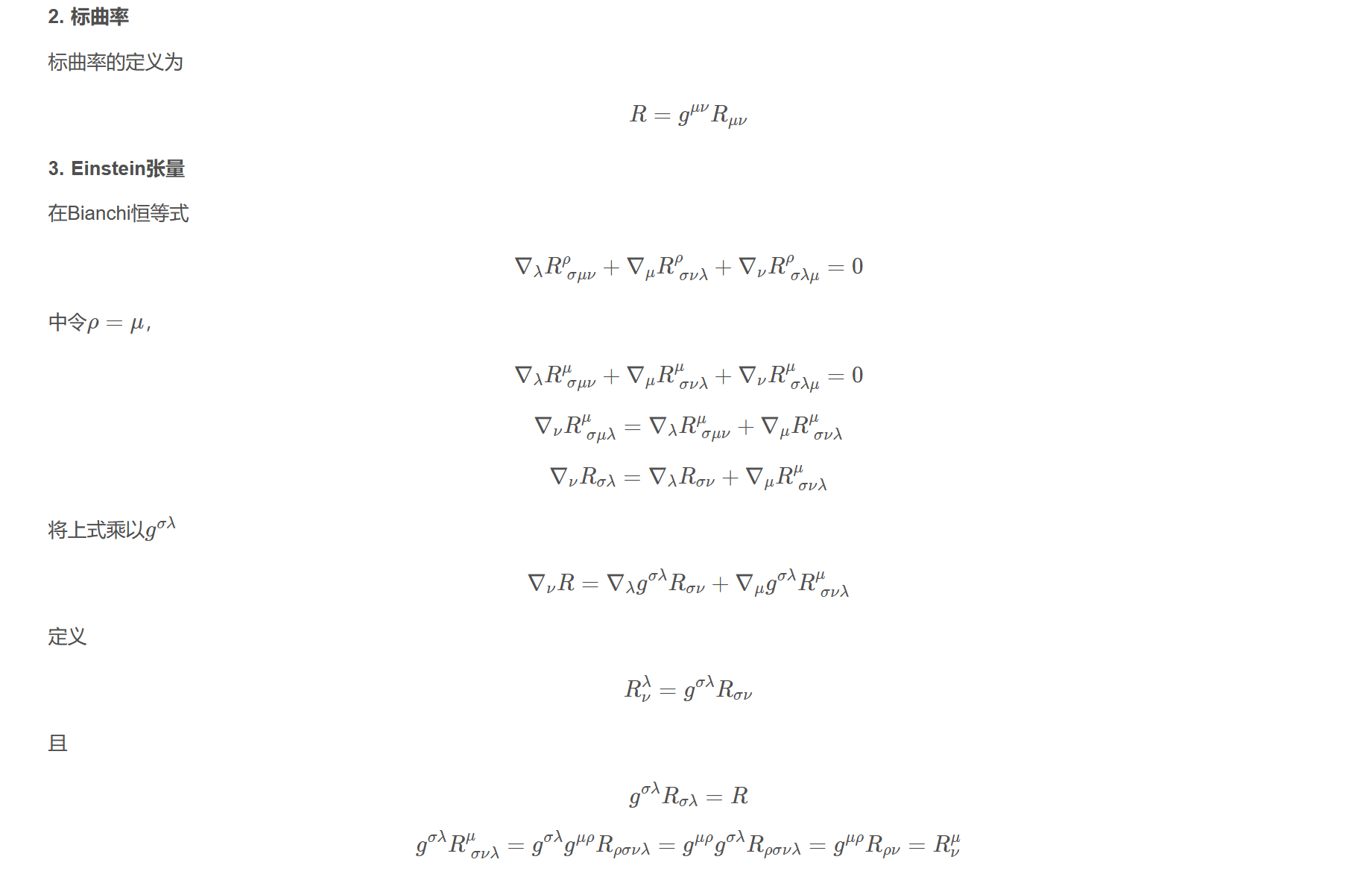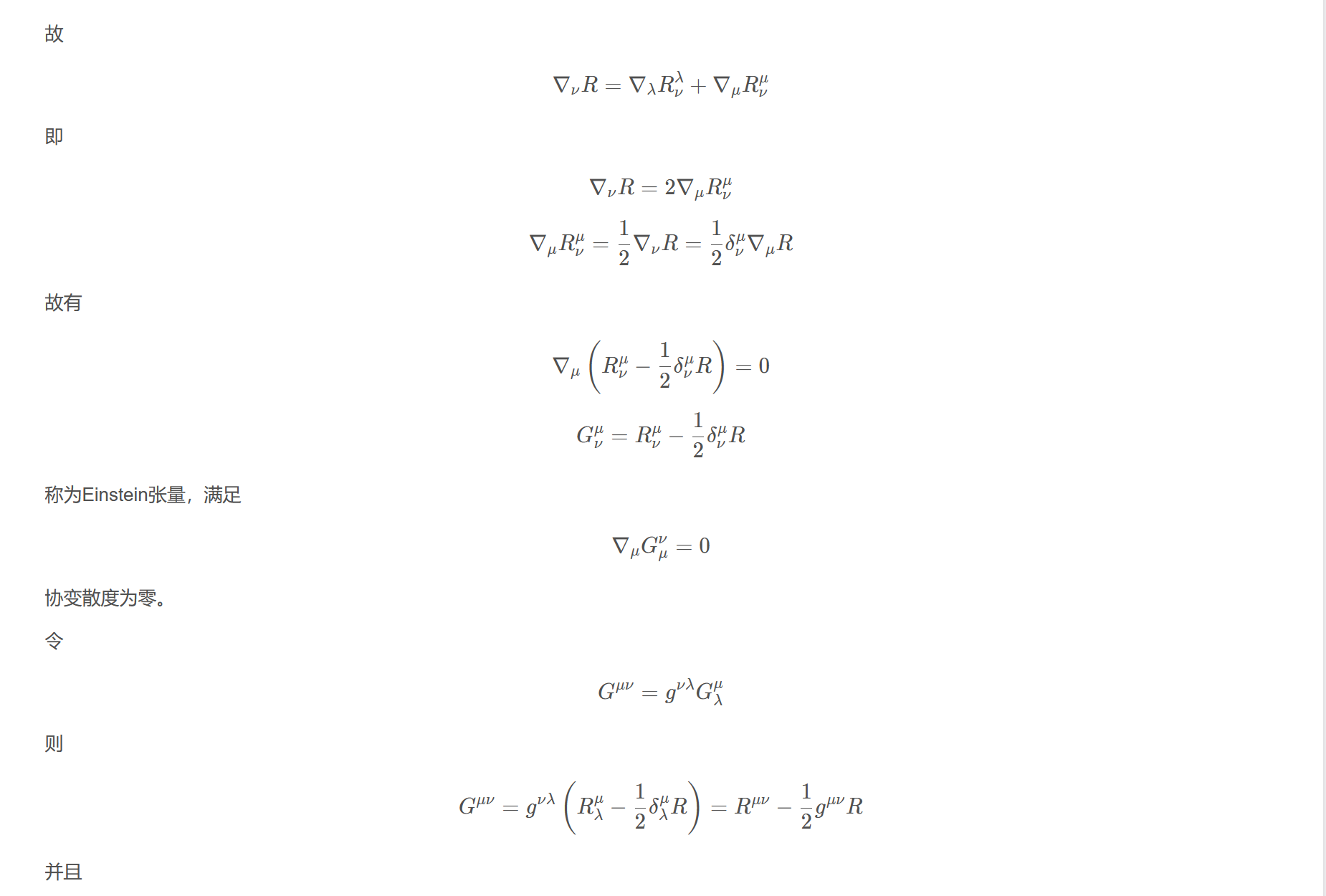物理

【广义相对论速成版】1. Riemann几何 1.6 Ricci张量、标曲率和Einstein张量

1. Ricci张量

Ricci张量的定义为

$$R_{\sigma\nu}=R_{~\sigma\lambda\nu}^{\lambda}\qquad \text{二阶张量}$$

或

$$R_{\sigma\nu}=g^{\lambda\mu}R_{\lambda\sigma\mu\nu}$$

由于

$$R_{\lambda\sigma\mu\nu}+R_{\lambda\mu\nu\sigma}+R_{\lambda\nu\sigma\mu}=0$$

乘以$g^{\lambda\mu}$

$$g^{\lambda\mu}R_{\lambda\sigma\mu\nu}+g^{\lambda\mu}R_{\lambda\mu\nu\sigma}+g^{\lambda\mu}R_{\lambda\nu\sigma\mu}=g^{\lambda\mu}R_{\lambda\sigma\mu\nu}+g^{\lambda\mu}R_{\lambda\nu\sigma\mu}=0$$

也即

$$g^{\lambda\mu}R_{\lambda\sigma\mu\nu}-g^{\lambda\mu}R_{\lambda\nu\mu\sigma}=0$$

故

$$R_{\sigma\nu}=R_{\nu\sigma}$$

为对称张量。

2. 标曲率

标曲率的定义为

$$R=g^{\mu\nu}R_{\mu\nu}$$

3. Einstein张量

在Bianchi恒等式

$$\nabla_{\lambda}R_{~\sigma\mu\nu}^{\rho}+\nabla_{\mu}R_{~\sigma\nu\lambda}^{\rho}+\nabla_{\nu}R_{~\sigma\lambda\mu}^{\rho}=0$$

中令$\rho=\mu$，

$$\nabla_{\lambda}R_{~\sigma\mu\nu}^{\mu}+\nabla_{\mu}R_{~\sigma\nu\lambda}^{\mu}+\nabla_{\nu}R_{~\sigma\lambda\mu}^{\mu}=0$$

$$\nabla_{\nu}R_{~\sigma\mu\lambda}^{\mu}=\nabla_{\lambda}R_{~\sigma\mu\nu}^{\mu}+\nabla_{\mu}R_{~\sigma\nu\lambda}^{\mu}$$

$$\nabla_{\nu}R_{\sigma\lambda}=\nabla_{\lambda}R_{\sigma\nu}+\nabla_{\mu}R_{~\sigma\nu\lambda}^{\mu}$$

将上式乘以$g^{\sigma\lambda}$

$$\nabla_{\nu}R=\nabla_{\lambda}g^{\sigma\lambda}R_{\sigma\nu}+\nabla_{\mu}g^{\sigma\lambda}R_{~\sigma\nu\lambda}^{\mu}$$

定义

$$R_{\nu}^{\lambda}=g^{\sigma\lambda}R_{\sigma\nu}$$

且

$$g^{\sigma\lambda}R_{\sigma\lambda}=R$$

$$g^{\sigma\lambda}R_{~\sigma\nu\lambda}^{\mu}=g^{\sigma\lambda}g^{\mu\rho}R_{\rho\sigma\nu\lambda}=g^{\mu\rho}g^{\sigma\lambda}R_{\rho\sigma\nu\lambda}=g^{\mu\rho}R_{\rho\nu}=R_{\nu}^{\mu}$$

故

$$\nabla_{\nu}R=\nabla_{\lambda}R_{\nu}^{\lambda}+\nabla_{\mu}R_{\nu}^{\mu}$$

即

$$\nabla_{\nu}R=2\nabla_{\mu}R_{\nu}^{\mu}$$

$$\nabla_{\mu}R_{\nu}^{\mu}=\frac{1}{2}\nabla_{\nu}R=\frac{1}{2}\delta_{\nu}^{\mu}\nabla_{\mu}R$$

故有

$$\nabla_{\mu}\left(R_{\nu}^{\mu}-\frac{1}{2}\delta_{\nu}^{\mu}R\right)=0$$

$$G_{\nu}^{\mu}=R_{\nu}^{\mu}-\frac{1}{2}\delta_{\nu}^{\mu}R$$

称为Einstein张量，满足

$$\nabla_{\mu}G_{\mu}^{\nu}=0$$

协变散度为零。

令

$$G^{\mu\nu}=g^{\nu\lambda}G_{\lambda}^{\mu}$$

则

$$G^{\mu\nu}=g^{\nu\lambda}\left(R_{\lambda}^{\mu}-\frac{1}{2}\delta_{\lambda}^{\mu}R\right)=R^{\mu\nu}-\frac{1}{2}g^{\mu\nu}R$$

并且

$$\nabla_{\mu}G^{\mu\nu}=0$$

可直接写成

$$\nabla_{\mu}\left(R^{\mu\nu}-\frac{1}{2}g^{\mu\nu}R\right)=0$$