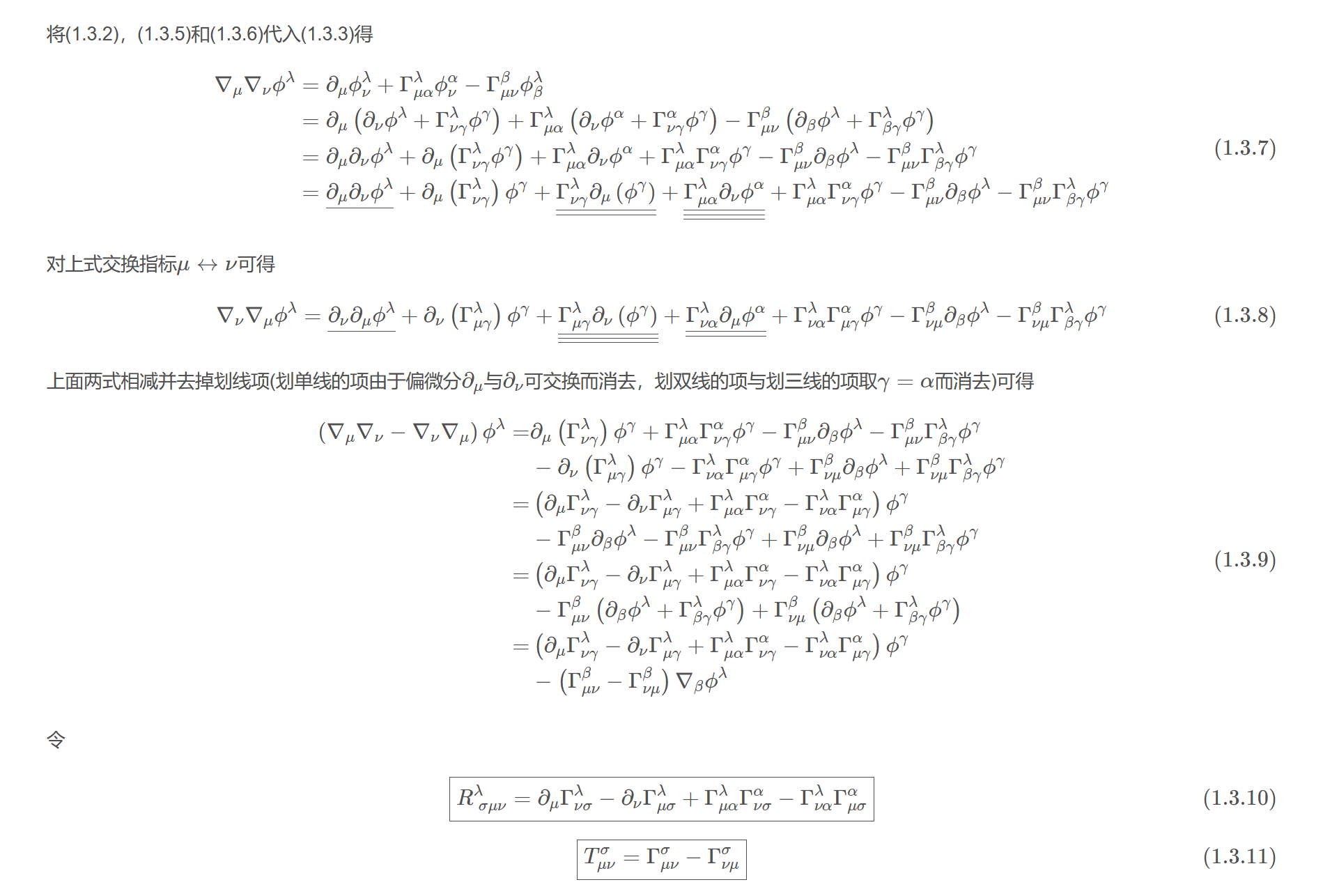物理

【广义相对论速成版】1. Riemann几何 1.3 曲率张量和挠率

1. 曲率和挠率的引入

设$\phi^{\lambda}$为逆变矢量，现在研究$\phi^{\lambda}$的二次协变微商

$$\left(\nabla_{\mu}\nabla_{\nu}-\nabla_{\nu}\nabla_{\mu}\right)\phi^{\lambda}$$

并由此定义曲率张量和挠率。

令

$$\phi_{\mu}^{\lambda}=\nabla_{\mu}\phi^{\lambda}=\partial_{\mu}\phi^{\lambda}+\Gamma_{\mu\gamma}^{\lambda}\phi^{\gamma}\tag{1.3.1}$$

$$\phi_{\nu}^{\lambda}=\nabla_{\nu}\phi^{\lambda}=\partial_{\nu}\phi^{\lambda}+\Gamma_{\nu\gamma}^{\lambda}\phi^{\gamma}\tag{1.3.2}$$

则

$$\nabla_{\mu}\nabla_{\nu}\phi^{\lambda}=\nabla_{\mu}\phi_{\nu}^{\lambda}=\partial_{\mu}\phi_{\nu}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\phi_{\nu}^{\alpha}-\Gamma_{\mu\nu}^{\beta}\phi_{\beta}^{\lambda}\tag{1.3.3}$$

$$\nabla_{\nu}\nabla_{\mu}\phi^{\lambda}=\nabla_{\nu}\phi_{\mu}^{\lambda}=\partial_{\nu}\phi_{\mu}^{\lambda}+\Gamma_{\nu\alpha}^{\lambda}\phi_{\mu}^{\alpha}-\Gamma_{\nu\mu}^{\beta}\phi_{\beta}^{\lambda}\tag{1.3.4}$$

将(1.3.2)中的指标变换$\lambda\to\alpha$，(1.3.1)中的指标变换$\mu\to\beta$，可得

$$\phi_{\nu}^{\alpha}=\nabla_{\nu}\phi^{\alpha}=\partial_{\nu}\phi^{\alpha}+\Gamma_{\nu\gamma}^{\alpha}\phi^{\gamma}\tag{1.3.5}$$

$$\phi_{\beta}^{\lambda}=\nabla_{\beta}\phi^{\lambda}=\partial_{\beta}\phi^{\lambda}+\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\tag{1.3.6}$$

将(1.3.2)，(1.3.5)和(1.3.6)代入(1.3.3)得

$$\begin{aligned}\nabla_{\mu}\nabla_{\nu}\phi^{\lambda}&=\partial_{\mu}\phi_{\nu}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\phi_{\nu}^{\alpha}-\Gamma_{\mu\nu}^{\beta}\phi_{\beta}^{\lambda}\\&=\partial_{\mu}\left(\partial_{\nu}\phi^{\lambda}+\Gamma_{\nu\gamma}^{\lambda}\phi^{\gamma}\right)+\Gamma_{\mu\alpha}^{\lambda}\left(\partial_{\nu}\phi^{\alpha}+\Gamma_{\nu\gamma}^{\alpha}\phi^{\gamma}\right)-\Gamma_{\mu\nu}^{\beta}\left(\partial_{\beta}\phi^{\lambda}+\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\right)\\&=\partial_{\mu}\partial_{\nu}\phi^{\lambda}+\partial_{\mu}\left(\Gamma_{\nu\gamma}^{\lambda}\phi^{\gamma}\right)+\Gamma_{\mu\alpha}^{\lambda}\partial_{\nu}\phi^{\alpha}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}\phi^{\gamma}-\Gamma_{\mu\nu}^{\beta}\partial_{\beta}\phi^{\lambda}-\Gamma_{\mu\nu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\\    &=\underline{\partial_{\mu}\partial_{\nu}\phi^{\lambda}}+\partial_{\mu}\left(\Gamma_{\nu\gamma}^{\lambda}\right)\phi^{\gamma}+\underline{\underline{\Gamma_{\nu\gamma}^{\lambda}\partial_{\mu}\left(\phi^{\gamma}\right)}}+\underline{\underline{\underline{\Gamma_{\mu\alpha}^{\lambda}\partial_{\nu}\phi^{\alpha}}}}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}\phi^{\gamma}-\Gamma_{\mu\nu}^{\beta}\partial_{\beta}\phi^{\lambda}-\Gamma_{\mu\nu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\end{aligned}\tag{1.3.7}$$

对上式交换指标$\mu\leftrightarrow\nu$可得

$$\nabla_{\nu}\nabla_{\mu}\phi^{\lambda}=\underline{\partial_{\nu}\partial_{\mu}\phi^{\lambda}}+\partial_{\nu}\left(\Gamma_{\mu\gamma}^{\lambda}\right)\phi^{\gamma}+\underline{\underline{\underline{\Gamma_{\mu\gamma}^{\lambda}\partial_{\nu}\left(\phi^{\gamma}\right)}}}+\underline{\underline{\Gamma_{\nu\alpha}^{\lambda}\partial_{\mu}\phi^{\alpha}}}+\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\gamma}^{\alpha}\phi^{\gamma}-\Gamma_{\nu\mu}^{\beta}\partial_{\beta}\phi^{\lambda}-\Gamma_{\nu\mu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\tag{1.3.8}$$

上面两式相减并去掉划线项(划单线的项由于偏微分$\partial_{\mu}$与$\partial_{\nu}$可交换而消去，划双线的项与划三线的项取$\gamma=\alpha$而消去)可得

$$\begin{aligned}\left(\nabla_{\mu}\nabla_{\nu}-\nabla_{\nu}\nabla_{\mu}\right)\phi^{\lambda}=&\partial_{\mu}\left(\Gamma_{\nu\gamma}^{\lambda}\right)\phi^{\gamma}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}\phi^{\gamma}-\Gamma_{\mu\nu}^{\beta}\partial_{\beta}\phi^{\lambda}-\Gamma_{\mu\nu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\\&-\partial_{\nu}\left(\Gamma_{\mu\gamma}^{\lambda}\right)\phi^{\gamma}-\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\gamma}^{\alpha}\phi^{\gamma}+\Gamma_{\nu\mu}^{\beta}\partial_{\beta}\phi^{\lambda}+\Gamma_{\nu\mu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\\=&\left(\partial_{\mu}\Gamma_{\nu\gamma}^{\lambda}-\partial_{\nu}\Gamma_{\mu\gamma}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}-\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\gamma}^{\alpha}\right)\phi^{\gamma}\\&-\Gamma_{\mu\nu}^{\beta}\partial_{\beta}\phi^{\lambda}-\Gamma_{\mu\nu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}+\Gamma_{\nu\mu}^{\beta}\partial_{\beta}\phi^{\lambda}+\Gamma_{\nu\mu}^{\beta}\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\\=&\left(\partial_{\mu}\Gamma_{\nu\gamma}^{\lambda}-\partial_{\nu}\Gamma_{\mu\gamma}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}-\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\gamma}^{\alpha}\right)\phi^{\gamma}\\&-\Gamma_{\mu\nu}^{\beta}\left(\partial_{\beta}\phi^{\lambda}+\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\right)+\Gamma_{\nu\mu}^{\beta}\left(\partial_{\beta}\phi^{\lambda}+\Gamma_{\beta\gamma}^{\lambda}\phi^{\gamma}\right)\\=&\left(\partial_{\mu}\Gamma_{\nu\gamma}^{\lambda}-\partial_{\nu}\Gamma_{\mu\gamma}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\gamma}^{\alpha}-\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\gamma}^{\alpha}\right)\phi^{\gamma}\\&-\left(\Gamma_{\mu\nu}^{\beta}-\Gamma_{\nu\mu}^{\beta}\right)\nabla_{\beta}\phi^{\lambda}\end{aligned}\tag{1.3.9}$$

令

$$\boxed{R_{~\sigma\mu\nu}^{\lambda}=\partial_{\mu}\Gamma_{\nu\sigma}^{\lambda}-\partial_{\nu}\Gamma_{\mu\sigma}^{\lambda}+\Gamma_{\mu\alpha}^{\lambda}\Gamma_{\nu\sigma}^{\alpha}-\Gamma_{\nu\alpha}^{\lambda}\Gamma_{\mu\sigma}^{\alpha}}\tag{1.3.10}$$

$$\boxed{T_{\mu\nu}^{\sigma}=\Gamma_{\mu\nu}^{\sigma}-\Gamma_{\nu\mu}^{\sigma}}\tag{1.3.11}$$

则(1.3.9)可表示为

$$\left(\nabla_{\mu}\nabla_{\nu}-\nabla_{\nu}\nabla_{\mu}\right)\phi^{\lambda}=[\nabla_{\mu},\nabla_{\nu}]\phi^{\lambda}=R_{~\sigma\mu\nu}^{\lambda}\phi^{\sigma}-T_{\mu\nu}^{\sigma}\nabla_{\sigma}\phi^{\lambda}\tag{1.3.12}$$

由(1.3.10)定义的$R_{~\sigma\mu\nu}^{\lambda}$称为曲率张量(Curvature tensor)(Riemann曲率张量有条件)，由(1.3.11)定义的$T_{\mu\nu}^{\sigma}$称为挠率张量(Torsion Tensor)。

由(1.3.10)和(1.3.11)很容易看出它们对$\mu,\nu$指标是反对称的

$$R_{~\sigma\mu\nu}^{\lambda}=-R_{~\sigma\nu\mu}^{\lambda}$$

$$T_{\mu\nu}^{\sigma}=-T_{\nu\mu}^{\sigma}$$

2. 以曲率和挠率为基础的流形分类

- Riemann-Cartan流形

$$R_{~\sigma\mu\nu}^{\lambda}\neq 0~,\qquad T_{\mu\nu}^{\sigma}\neq 0$$

- Riemann流形

$$R_{~\sigma\mu\nu}^{\lambda}\neq 0~,\qquad T_{\mu\nu}^{\sigma}= 0$$

- Weizenb$\mathrm{\"{o}}$ck流形

$$R_{~\sigma\mu\nu}^{\lambda}= 0~,\qquad T_{\mu\nu}^{\sigma}\neq 0$$

曲率张量和挠率张量都是由联络$\Gamma_{\mu\nu}^{\lambda}$构成的。

虽然$\Gamma_{\mu\nu}^{\lambda}$不是张量，但由它可以构成张量$R_{~\sigma\mu\nu}^{\lambda}$和$T_{\mu\nu}^{\lambda}$。