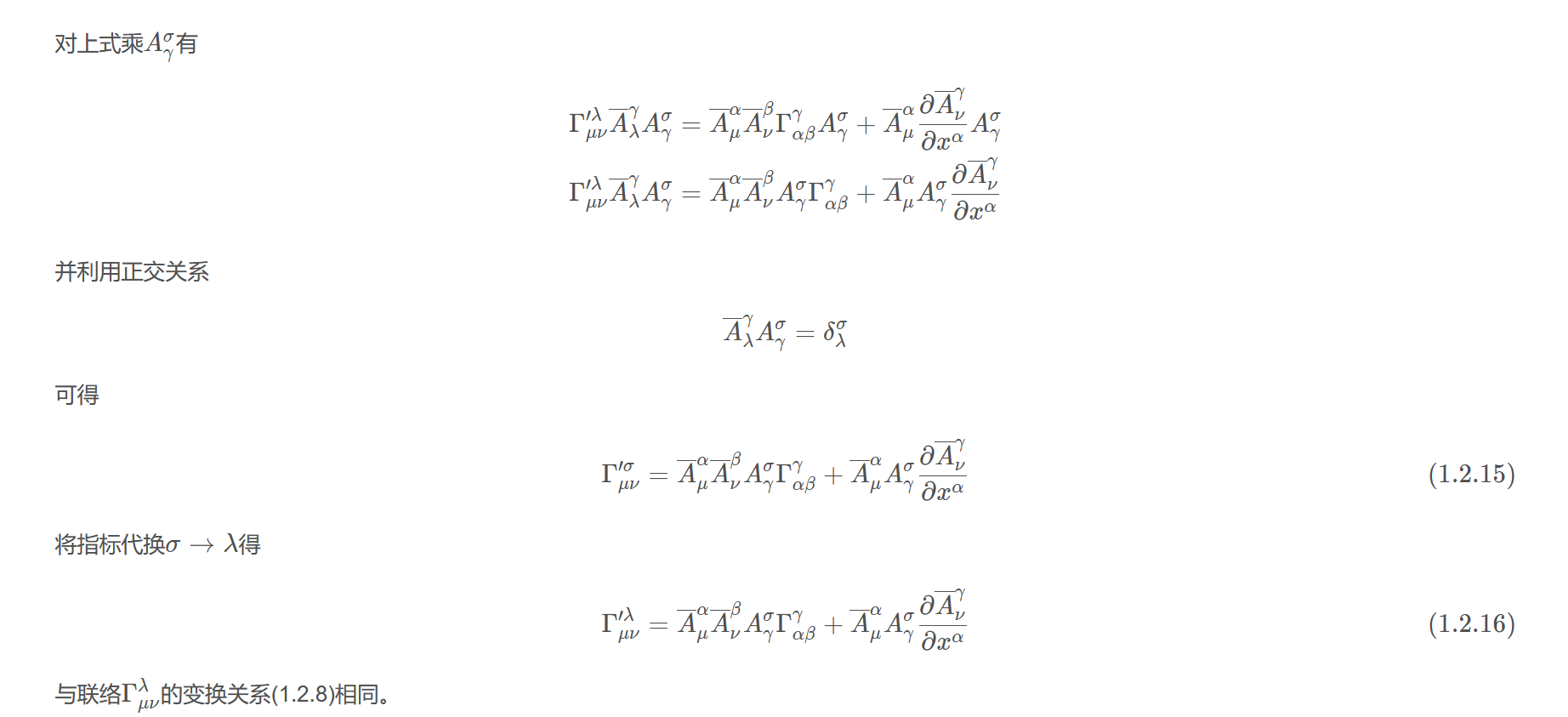物理

【广义相对论速成版】1. Riemann几何 1.2 协变微商(2)

2. 协变矢量的协变微商

协变矢量$\phi_{\nu}$的协变微商

$$\nabla_{\mu}\phi_{\nu}\tag{1.2.9}$$

要求具有二阶协变张量的特征，即：

$$\nabla_{\mu}^{\prime}\phi_{\nu}^{\prime}=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\nabla_{\alpha}\phi_{\beta}\tag{1.2.10}$$

$\nabla_{\mu}\phi_{\nu}$具有如下形式

$$\boxed{\nabla_{\mu}\phi_{\nu}=\frac{\partial\phi_{\nu}}{\partial x^{\mu}}-\Gamma_{\mu\nu}^{\lambda}\phi_{\lambda}}\tag{1.2.11}$$

则

$$\nabla_{\mu}^{\prime}\phi_{\nu}^{\prime}=\frac{\partial \phi_{\nu}^{\prime}}{\partial\overline{x}^{\mu}}-\Gamma_{\mu\nu}^{\prime\lambda}\phi_{\lambda}^{\prime}\tag{1.2.12}$$

将

$$\phi_{\nu}^{\prime}=\overline{A}_{\nu}^{\beta}\phi_{\beta}$$

和

$$\frac{\partial}{\partial \overline{x}^{\mu}}=\overline{A}_{\mu}^{\alpha}\frac{\partial}{\partial x^{\alpha}}$$

代入(1.2.12)可得

$$\begin{aligned}\nabla_{\mu}^{\prime}\phi_{\nu}^{\prime}&=\overline{A}_{\mu}^{\alpha}\frac{\partial}{\partial x^{\alpha}}\left(\overline{A}_{\nu}^{\beta}\phi_{\beta}\right)-\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}\\&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\frac{\partial\phi_{\beta}}{\partial x^{\alpha}}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\beta}}{\partial x^{\alpha}}\phi_{\beta}-\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}\end{aligned}\tag{1.2.13}$$

另一方面，由(1.2.10)知

$$\begin{aligned}\nabla_{\mu}^{\prime}\phi_{\nu}^{\prime}&=\overline{A}_{\mu}^{\nu}\overline{A}_{\nu}^{\beta}\nabla_{\alpha}\phi_{\beta}\\&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\left(\frac{\partial \phi_{\beta}}{\partial x^{\alpha}}-\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}\right)\\&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\frac{\partial \phi_{\beta}}{\partial x^{\alpha}}-\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}\end{aligned}\tag{1.2.14}$$

比较(1.2.13)与(1.2.14)两式可得

$$\begin{aligned}\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\frac{\partial\phi_{\beta}}{\partial x^{\alpha}}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\beta}}{\partial x^{\alpha}}\phi_{\beta}-\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\frac{\partial \phi_{\beta}}{\partial x^{\alpha}}-\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}\\\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\beta}}{\partial x^{\alpha}}\phi_{\beta}-\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}&=-\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}\\\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\beta}}{\partial x^{\alpha}}\phi_{\beta}\end{aligned}$$

将等号右边最后一项指标代换$\beta\to\gamma$得

$$\begin{aligned}\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}\phi_{\gamma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}\phi_{\gamma}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}\phi_{\gamma}\\\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}\end{aligned}$$

对上式乘$A_{\gamma}^{\sigma}$有

$$\begin{aligned}\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}A_{\gamma}^{\sigma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}\Gamma_{\alpha\beta}^{\gamma}A_{\gamma}^{\sigma}+\overline{A}_{\mu}^{\alpha}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}A_{\gamma}^{\sigma}\\\Gamma_{\mu\nu}^{\prime\lambda}\overline{A}_{\lambda}^{\gamma}A_{\gamma}^{\sigma}&=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}A_{\gamma}^{\sigma}\Gamma_{\alpha\beta}^{\gamma}+\overline{A}_{\mu}^{\alpha}A_{\gamma}^{\sigma}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}\end{aligned}$$

并利用正交关系

$$\overline{A}_{\lambda}^{\gamma}A_{\gamma}^{\sigma}=\delta_{\lambda}^{\sigma}$$

可得

$$\Gamma_{\mu\nu}^{\prime\sigma}=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}A_{\gamma}^{\sigma}\Gamma_{\alpha\beta}^{\gamma}+\overline{A}_{\mu}^{\alpha}A_{\gamma}^{\sigma}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}\tag{1.2.15}$$

将指标代换$\sigma\to\lambda$得

$$\Gamma_{\mu\nu}^{\prime\lambda}=\overline{A}_{\mu}^{\alpha}\overline{A}_{\nu}^{\beta}A_{\gamma}^{\sigma}\Gamma_{\alpha\beta}^{\gamma}+\overline{A}_{\mu}^{\alpha}A_{\gamma}^{\sigma}\frac{\partial \overline{A}_{\nu}^{\gamma}}{\partial x^{\alpha}}\tag{1.2.16}$$

与联络$\Gamma_{\mu\nu}^{\lambda}$的变换关系(1.2.8)相同。

3. 二阶张量的协变微商

我们记

$$\partial_{\mu}\equiv\frac{\partial}{\partial x^{\mu}}$$

同样很容易推广到(协变、逆变、混合)二阶张量的协变微商为

$$\begin{aligned}\nabla_{\mu}\phi_{\alpha\beta}=&\partial_{\mu}\phi_{\alpha\beta}-\Gamma_{\mu\alpha}^{\nu}\phi_{\nu\beta}-\Gamma_{\mu\beta}^{\nu}\phi_{\alpha\nu}\\\nabla_{\mu}\phi^{\alpha\beta}=&\partial_{\mu}\phi^{\alpha\beta}+\Gamma_{\mu\nu}^{\alpha}\phi^{\nu\beta}+\Gamma_{\mu\nu}^{\beta}\phi^{\alpha\nu}\\\nabla_{\mu}\phi_{\beta}^{\alpha}~=&\partial_{\mu}\phi_{\beta}^{\alpha}~~+\Gamma_{\mu\nu}^{\alpha}\phi_{\beta}^{\nu}~-\Gamma_{\mu\beta}^{\nu}\phi_{\nu}^{\alpha}\end{aligned}$$