物理

#一些有趣的几何知识【分形&四维多胞体】

8.20整体修补

8.19多胞体二更

8.2多胞体一更

7.31分形四更

7.24分形三更

7.21分形二更

7.4分形一更

点个赞点个收藏支持一下帖主谢谢😭

【正片开始】

分形部分：

分形，一个很好玩也很强大的几何分支，虽然有些地方有点超模连主播也不会，但包好玩的😋👍

无论如何记住这个入的名字，虽然后面讲不到他👀：上世纪70年代一己之力创立分形理论的---芒德布罗(Mandelbrot)

1924-2010，波兰的立陶宛裔犹太人🤓

有人就要说了：主播主播你一开始就介绍个入，那分形到底是个啥？😡👊

定义扔在这里：

分形，具有以非整数维形式填充空间的形态特征。

说人话：就是一个粗糙零碎的几何形状，能分出若干个部分，其中严格自相似分形分出的部分就是整体缩小的形状😋

然后我们来瞅一瞅实例：

非常经典的自相似分形---谢尔宾斯基三角形！

而它是怎么构造的呢？这里给出一种最简单直观的方法：

1. 画一个大的等边三角形

2. 连接各边中点，将大三角形分成4个较小的等边三角形

3. 移除中间的那个小三角形

4. 对剩下的3个小三角形重复步骤2-3

5. 无限重复

其他的先不多说，往下看🤓

然后我们再来看一个例子：科赫雪花(由若干条科赫曲线组成)

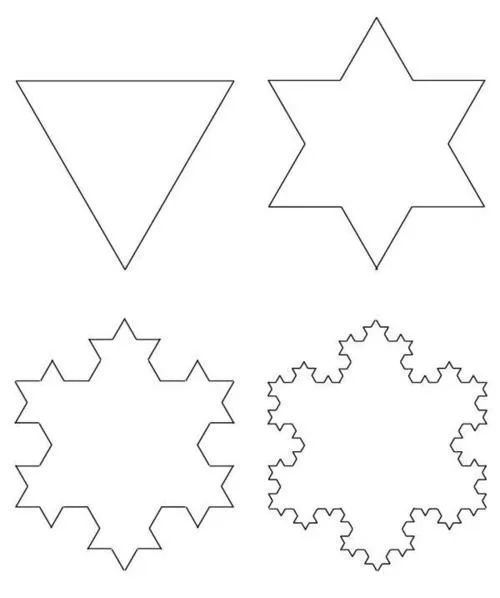
构造步骤上图已经给出了😋

大概描述一下：

1.画一个等边三角形

2.将每条边三等分，在中间段向外作等边三角形

3.移除中间段

循环此步骤就能看到上图的分形了👍

(以下latex均为图片，一些主播不会打问的AI所以会有奇怪的缩进😭

这里给出科赫曲线n次与∞次迭代：(为了方便修改放图片)

==============================================

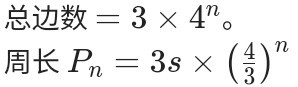
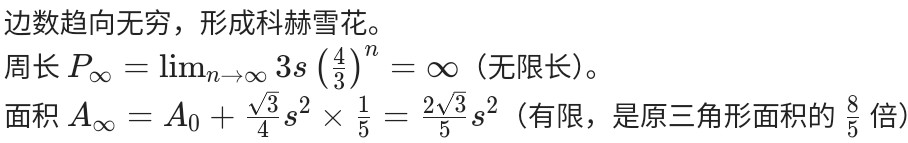
大家最关注的是分形的维数吧？这也是分形最有魅力的地方😋

普通的拓扑维数是怎么定义的呢：

它是确定整个图形中点的位置所需要的参数的个数。

一个点不需要参数，就是0，

线需要一个参数来确定位置，就是1，

同理，平面需要两个参数，空间需要三个参数，我们所说的2维，3维便是这个😋👊

但分形显而易见无法用拓扑维数去判定，于是豪斯多夫在1910年提出了分形维的概念！

豪斯多夫维数(Hausdorff dimension)，其描述了分形的复杂性。

这里就给出自相似分形维数的公式了，反正够算😎🙌

接下来，各位来算一算科赫雪花的维数吧～😋👍

AI帮忙码的latex奇奇怪怪的(吐槽💦

也表明了科赫雪花周长无限长，细节无限丰富，但面积有限💦

通过公式，就能算出自相似分形的维数啦～知道子部分数量N与缩放比r就能代入公式了😋

第一个介绍的谢尔宾斯基三角形如下：

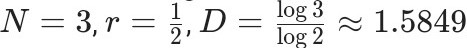
如果要计算非严格自相似分形，如地形，推荐使用盒维数（Box-counting Dimension）计算🤓👊

公式如下，略显复杂💦

这里就不给出计算示例了，大家一般用第一种就可以了💦

也不知道该说点啥了，来看看分形在自然科学中有多么强大😋👍

生物学：

血管系统：分形分支优化氧气输送（维数 ≈ 2.7）

肺支气管：自相似结构最大化表面积（人类肺维数 ≈ 2.97）

地球科学：海岸线测量（芒德布罗1967）：英国海岸线维数 ≈ 1.25，长度随测量尺度增大而发散。

物理学：

渗流理论：临界状态下孔隙的分形维数。

布朗运动：轨迹的盒维数 = 2（尽管拓扑维数为 1）🤔

=====================================================

还有分形在技术领域的应用😋

计算机图形学：

地形生成：中点位移法（Midpoint Displacement）模拟山脉（维数可控）

特效设计：火焰、云朵的粒子系统（基于 IFS）

天线工程：

分形天线：利用自相似性实现多频段/小型化（如科赫曲线天线）

还是很超模的😰，生活中处处是分形！

那分形就到这里了，接下来登场的是四维多胞体！

-------------------------------------------------------------------------------------------------------------------------------------分

===================================================================割

-------------------------------------------------------------------------------------------------------------------------------------线

四维多胞体部分：

来看看正多胞体吧，定义是是四维空间中的规则几何体，是三维正多面体的高维类比。

它们具有对称的胞，面，棱和顶点，其中的“胞”，就是三维的正多面体～😋

它们只有六种类型：正五胞体，正八胞体(超立方体)，正十六胞体，正二十四胞体，正一百二十胞体，正六百胞体。

如果我们想看到其在三维空间的类比，就要使用施莱格尔投影🤓👆

我们要在多胞体的外接球(当然对于四维，外接的是超球)上取一点作透视投影，就能出现它的三维投影。

再将三维投影投影到二维上，就能以图片的形式看到它了😋🙌

由于蓝牙传图片被禁用，只能拍一下正五胞体的投影了💦

因为板砖影像极其抽象和光线问题，效果不是很好😭

我们很容易得到得到正五胞体的一些数据：

胞(正四面体)数：5，面(正三角形)数：10，棱数：10，顶点数：5

此外，常用的还有球级投影，这个不多说了，就是将正五胞体表面膨胀变成超球投影到无穷大的平面上🤓

还有二维线架正投影，其实是写入五个点的坐标投影得到的，但正五胞体的这种投影实在是太简单了😋

就是作一个正五边形然后每两点两两连线就是了🤓，所以只能表现其点与线之间的连接关系👀

一个四维几何体的二维正投影不止一种，不同的投影用来抽象表现其不同的特性，可以去英文维基百科看看👍

好了投影也讲的差不多了😋👍

不知道讲啥了，说下二胞角😋

吐槽一下，不小心推出去给我吞了😭啊啊啊啊啊啊啊啊啊啊码了好久✋😭✋

知周所众，多面体上有二面角。。。这都不知道回去重修立体几何！😡👊

那么多胞体就有二胞角，就是两个立体的夹角啦😋

可是求二胞角，求导要用到四维解析几何，驻波也是看的头皮发麻😭

唉没事🤓👆

先要认识一下正单形这个概念：指n维空间中由n+1个点构成的几何体，使这些点满足每两个点距离相等。

从0维开始依次对应点，线段，正三角形，正四面体，正五胞体等

(单形是什么？说人话就是该维度中构造最简单的几何体～

那我们用二维正单体和三维正单体来类比四维正单体：正五胞体不就行了🤓👍

正三角形的二边角，就是夹角为60°，用反三角函数表示就是arccos (1/2)  ；             为了方便修改不用latex哈💦

正四面体的二面角，约为70.53°，就是arccos (1/3) ；

那么正五胞体的二胞角，自然就是arccos (1/4)啦！计算器会告诉我们答案：约是75.52°🤓👍

这要是看不懂我也没办法了(瘫倒

求支持，点个赞点个收藏吧😭😭😭

The end.