物理

光的折射定律——最短路径

先上图

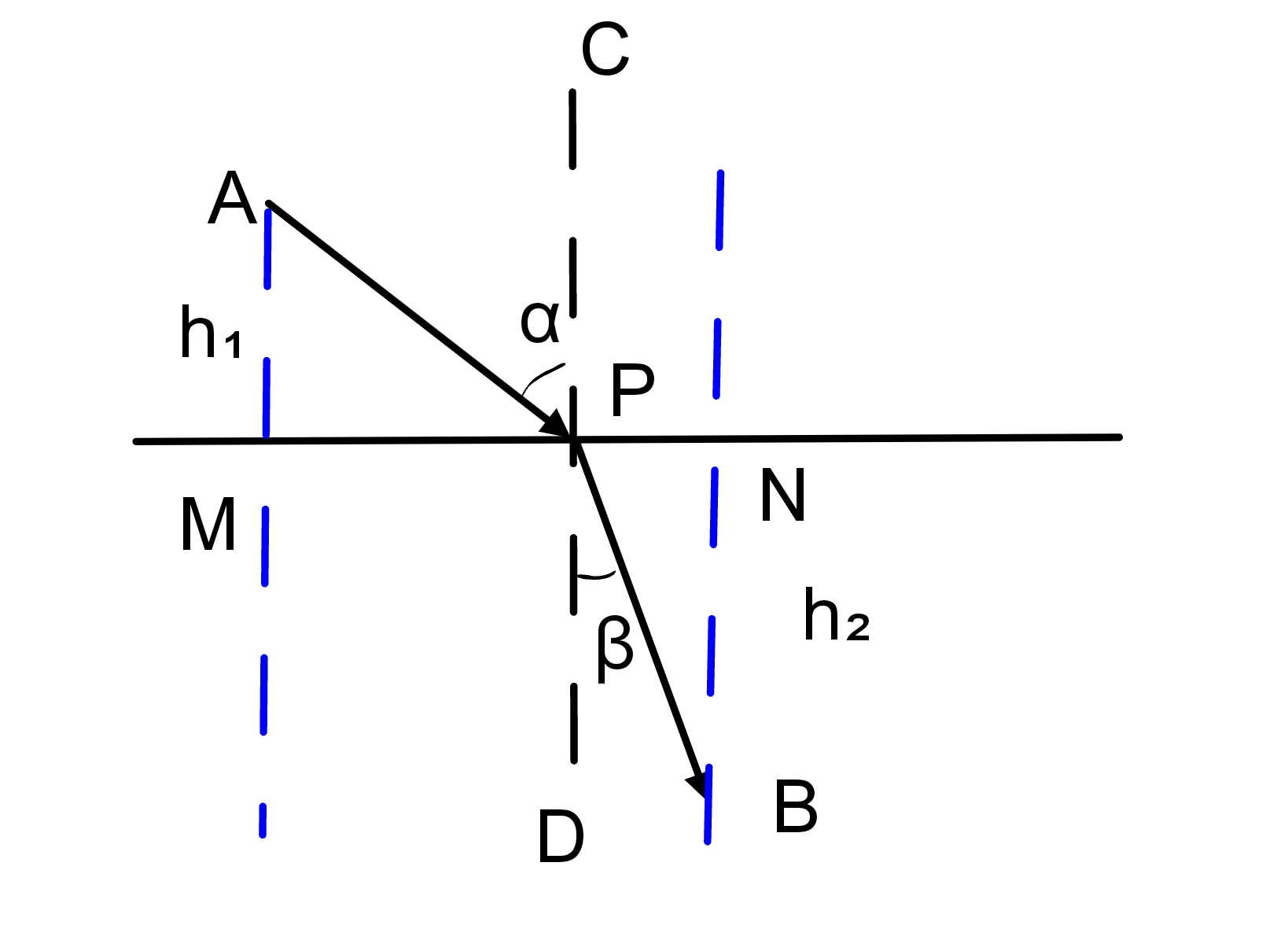
$CD$是法线，$P$是折射点，$A$是入射光线出发点，$B$是折射光线终止点

光线在上方介质中速度为$v_1$，在下方介质中速度为$v_2$

我们由费马定理可得：光总延耗时最短的路径走，那么从$A到B$，光怎样走耗时最短呢？

首先，我们如图已知$AM=h_1,BN=h_2,MN=l,MP=x,角APC=α,角BPD=β$

那么光线从A到B所花时间为：

$t(x)=\frac{1}{v_1}\sqrt{h_1^2+x^2}+\frac{1}{v_2}\sqrt{h_2^2+(l-x)^2}$ ，$x∈[0,l]$

那么我们要求$t(x)$最小值，先求$t对x$的导数

$t'(x)=\frac{1}{v_1}\frac{x}{\sqrt{h_1^2+x^2}}-\frac{1}{v_2}\frac{l-x}{\sqrt{h_2^2+(l-x)^2}}$ 

由于$t'(0)小于0,t'(l)大于0$

且$t''(x)=\frac{1}{v_1}\frac{h_1^2}{(h_1^2+x^2)^\frac{3}{2}}+\frac{1}{v_2}\frac{h_2^2}{[h_2^2+(l-x)^2]^\frac{3}{2}}$ 大于$0$

所以$t'(x)在[0,l]$上有唯一零点$x_0$，

且$t''(x)大于0$，

可知$x_0$为最小值点

即$x_0$满足$t'(x_0)=0$，即

$\frac{1}{v_1}\frac{x_0}{\sqrt{h_1^2+x_0^2}}=\frac{1}{v_2}\frac{l-x_0}{\sqrt{h_2^2+(l-x_0)^2}}$ 

由图知$\frac{x_0}{\sqrt{h_1^2+x_0^2}}=\sin α$,$\frac{l-x_0}{\sqrt{h_2^2+(l-x_0)^2}}=\sin β$

所以$\frac{\sin α}{v_1}=\frac{\sin β}{v_2}$

我们就得到了折射定律：

$n_{12}=\frac{\sin α}{\sin β}=\frac{v_1}{v_2}$