物理

[论坛资料室]用深井方法解题——平面直角坐标系内三角形

（OI，初中牲，不进来看一眼？）

在裂谷最深处传来悠扬的悲歌

在这横平竖直的坐标监狱里，求解从未停止

但该失去的总归要失去，就像裂谷的形成一般，冷漠，悲凉

敬未来，敬当下，敬过往

（一定要我一个理科生把话写的这么文艺是吧，豪豪豪）（拿出当年写小说的感觉了）

Ⅰ    一次函数

对于一些奇形怪状的三角形，我们往往需要用到很复杂的计算（当然，只针对初中）

而初一的这种类型的题目几乎已经是压轴题的水评了（没办法，还有个动角）

例:

（24题第3问）

对于这种题目，一般的做法应该是这样（本人卷子）：

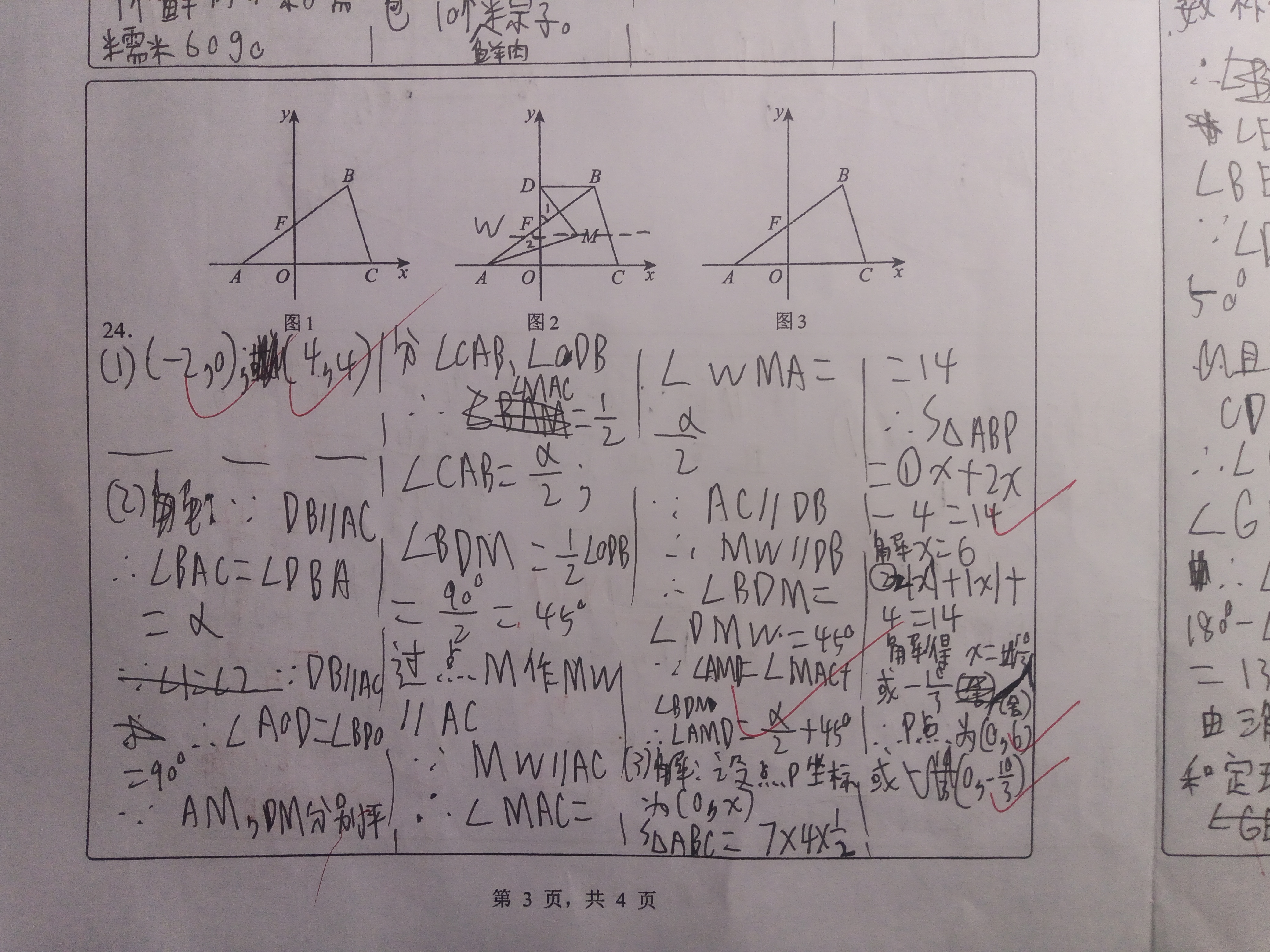
即分类讨论，利用三角形面积之和相等以及点的坐标来求点的坐标

这个过程需要大量计算，也较为复杂

但其实，上过zx的入都知道，平面直角坐标系内不只有三角形，还有......

3

2

1

没错，$huge{一次函数}$

在此题中，我们可以直接求出点F的坐标

∵A,B在同一直线上

∴可利用A,B坐标得出方程

具体过程如下：

设A,B的方程为${y=kx+b}$

∵点F在y轴上

∴点F的坐标为（0，？）

又∵点A的坐标为(—2，0），点B的坐标为（4，4）

∴$\begin{cases}0=—2k+b\\4=4k+b\end{cases}$（会了！）

解得 k=2;b=—4

带入F点，因为它在y轴上，所以y=0，然后就能算出点P的两种情况了（即用yP±yF后求三角形面积）

Ⅱ    皮克定理

$sout{在生活中}$在考试中，我们时常会遇到类似这样的题目：

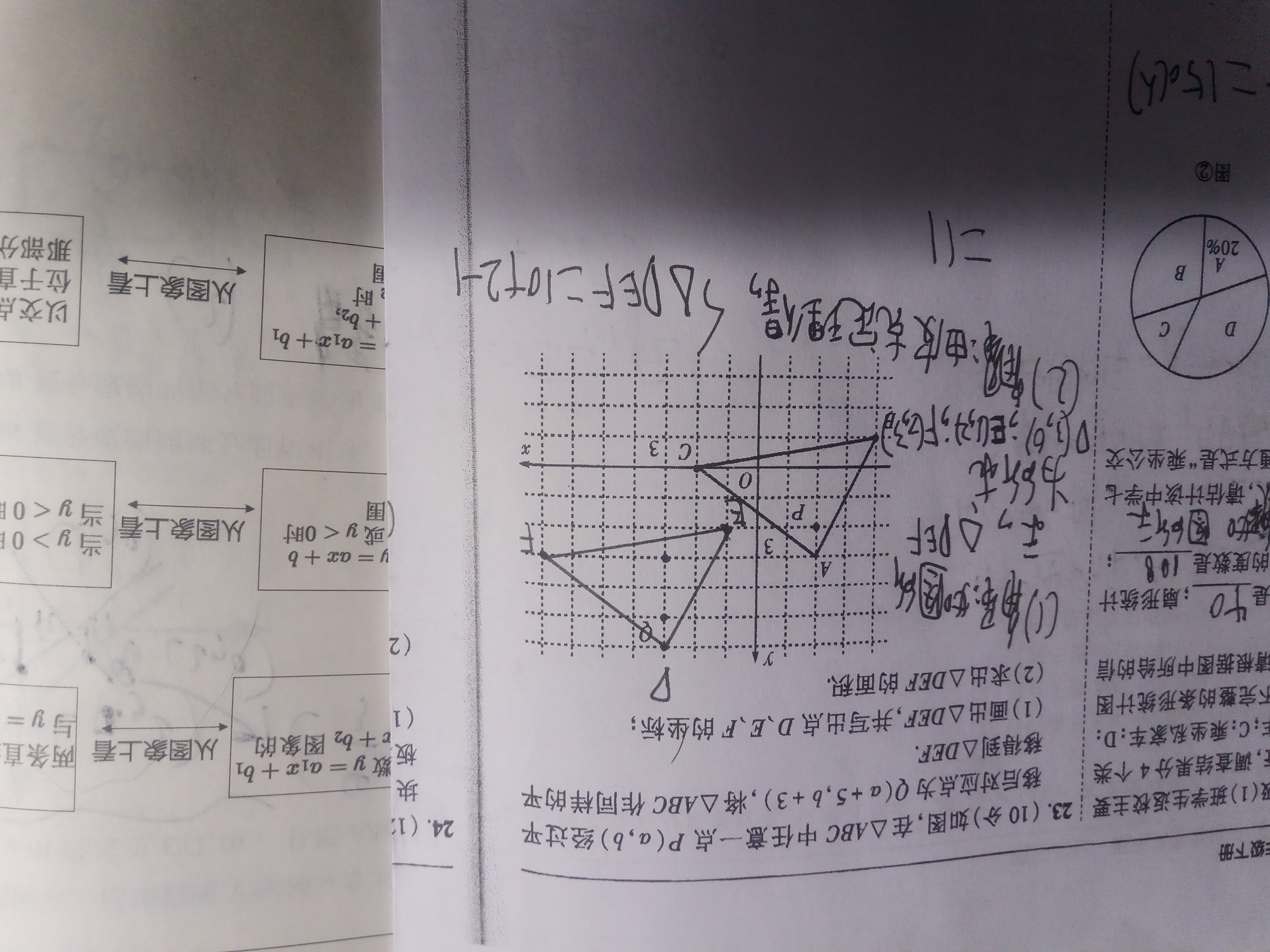
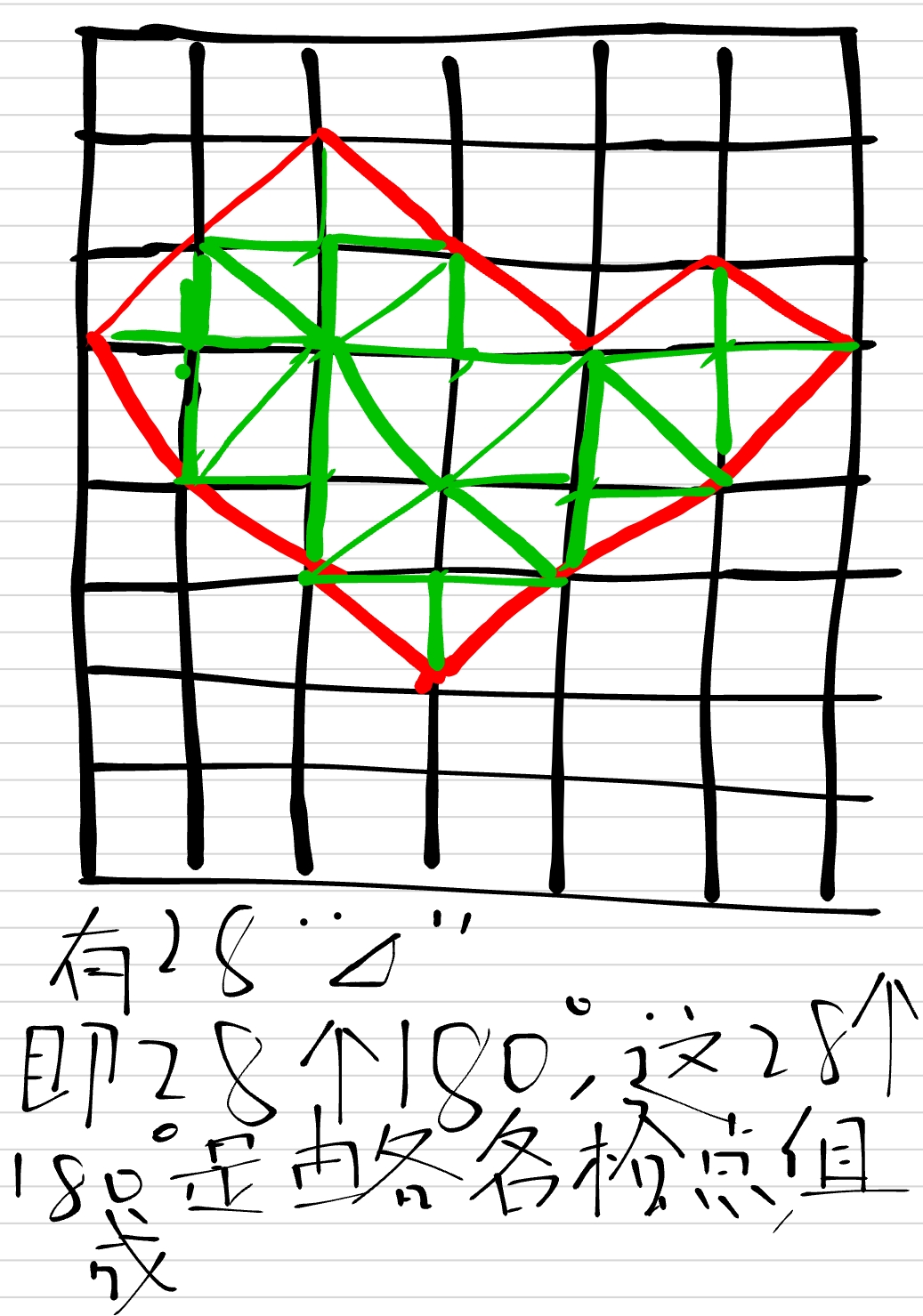
（拍摄问题致歉）（本人作业，平常字不长这样）

即在有方格的平面直角坐标系中求三角形面积，但同时，这三角形又长的很丑（就是不落在数轴上的意思）

在这种情况下，我们可以使用一种十分amazing的定理：皮克定理

皮克定理的内容大致是：在一个方格图中，三角形面积=内部格点数+1/2外部格点数—1

这里的内格点数指三角形内的格点数量（记住是三角形内），外格点数指三角形三边上经过的格点数

但这种方法有个唯一的缺陷，那便是：

如果自己画图，考虑到误差问题，很难确定某个点是否正好落在三角形边上，所以只能用试卷上给的图

同时，由于证明需用到欧拉公式，所以在初中阶段直接使用时（就是我这么用），会被扣一分

综上，此方法仅限检查或作答时辅助，不可直接当作过程（我的那是错误示范）

Ⅲ    铅垂法

应用很广的一种做法，一般配合其他方法食用😋😋😋

例：（题忘带了，明天补）

在这种三角形中，我们可以发现点B和点P在同一直线上（虽然并未画出，但条件给了）

然后，不管你用什么方法，连BP，求出BP长

因为B点坐标已给出，所以只需求出点P即可

求完后得到两个好看点的三角形，然后结合点A与C坐标，求出两三角形面积

最后相加，得到结果

过程例：（理由同上）

学完了这三种方法，你这个初中的平面直角坐标系内三角形基本没啥问题啦

但记住，学以致用，所以作者找了些例题，有难有易，可以做一下～：（理由同上）

顺便问一下@5汉爱学习@5汉（不知道是哪个），这个帖可以吗🤔，如果知识点太低级我就删帖，再回去沉淀沉淀

欢迎讨论、纠错、睿频 

（明天再补充一些，今天太晚了）