物理

【论坛资料室】一命速通——集合与逻辑用语

根据一些新手轮同学的需求，开了个这个坑♿♿♿

高数的帖子等填完这个再更😋

$\Huge{更新进度：\color{cyan}{60\%}}$

——————————————————————————以下是正文—————————————————————————

$\huge{引言}$

集合和逻辑用语，其实本质不同，但有一些微妙的关系

而且均篇幅较小，所以我总结为一个帖子

主要是这些东西不需要什么基础，但是以后特别常用

非常简单，新手轮都看得懂

(此处省略一万字......)

$\huge{Part~01.集合}$

$\LARGE{Ⅰ.最基本的东西！}$

我们如果想要学习高等数学，就难免设计无穷

但是，前三次数学危机都是无穷引发的

那想要了解无穷，就首先知道数的本质

数的本质又是什么？就是集合

$集合首先是由德国的一位数学家格奥尔格\cdot 康托尔(Georg~Cantor)提出的，他就是集合论的创始人.$

但是集合到底是什么呢？先看看集合的定义吧😋：

一般地，我们把研究对象统称为$\color{blue}{元素}$ $(element)$，把一些元素组成的总体叫做$\color{blue}{集合}$ $(set)(简称集)$.

元素通常用小写字母表示，集合通常用大写字母表示

这里面的元素和集合可以是任何东西，比如地球上的生物就可以构成一个集合

元素甚至也可以是一个不等于这个集合的集合

主播主播，为什么元素不能为集合本身🤔？我们后面再解决♿

$特别地，如果集A的每个元素都为一个集合，那我们称A为一个\color{blue}{族}$或$\color{blue}{集族}$.

集合中，最常用的是数集，即所以元素均为数的集合

其次就是点集，所以元素均为坐标系上的点

一个元素a和集合A有两种关系👇：

$假定a为A的元素，称a属于A，记作a\in A；a不属于A，记作a\notin A.$

但是，有一种特殊的集合，不含任何元素，它就是空集，用$\varnothing$表示.

好，我们来了解一下常用的几个集合👇：

$1.\mathbb{N}(自然数集)$

$2.\mathbb{N}^*或\mathbb{N}_+(正整数集)$

$3.\mathbb{Z}(整数集)$

$4.\mathbb{Q}(有理数集)$

$5.\mathbb{R}(实数集)$

$6.\mathbb{C}(复数集)~~~~~~(目前不用)$

表示一个集合，有一下几个方法：

$1.列举法：最简单的方法，把元素都写在一起，中间用，分割，两边用\{\} 包裹.比如A=\{ 1，2，3\} 🤓.$

$2.描述法：用条件定义集合内的元素，|后是元素的条件$.

$e.g.\mathbb{Q}=\frac{p}{q}|p，q\in \mathbb{Z}.$

$3.venn图法：小学就学过，画个圈把元素写在里面，一点也不抽象.$

$4.区间表示法：开区间(a，b)为集合\{ x|a\lt x\lt b\} ，闭区间\left[ a，b\right]为集合\{ x|a\le x\le b\}$

当然也可以结合起来♿：$e.g.[1，+\infty )$$

而且，一个集合内的元素有以下几个性质：

$1.确定性：任何元素都能明确判断是否属于集合$

比如说：长得帅的人就不是一个集合

因为“帅”这个概念还是太抽象了，到底长什么样才叫帅？单拎一个元素出来，有人认为属于这个集合，也有人不认为

所以他到底属不属于这个集合？无法确定，于是“长的帅的人”就不是一个集合

$2.互异性：集合中的元素唯一，不重复$

$3.无序性：元素排列无顺序要求.如\{1，2，3\} =\{ 2，3，1\}$

集合与集合之间的关系：

$如果有集合A和集合B，若A包含于B，即A中任意元素a\in B，称A为B的子集，记作A\subseteq B$

小结论：如果$A\subseteq B，B\subseteq A，则A=B$.

$主播主播，那集合A中的每个元素都属于A(疑似废话)，那么A\subseteq A？$

$\color{red}{没错！}$你已经发现了一个重要的东西，但是还有另一个：$\varnothing\subseteq A.$🤓

好，那如果$A\subseteq B，则可能A=B，但是我不想让A=B，该怎么办？$

$\sout{那就重开}我们称A真包含于B，A是B的真子集，记作A\subsetneqq B.$

好的，下前面的小问题，就是这个问题引发了罗素悖论，从而导致第三次数学危机

罗素悖论是啥？我们先看看它的通俗版——理发师悖论：

在一个小镇上有一个理发师，他说：“我只给所有不给自己刮胡子的人刮胡子！”那问题来了：他该不该给自己刮胡子？

如果你仔细想想，他刮不刮都是矛盾的😓

罗素悖论和这个就很相似：给定一个集族R，由所有不属于自身的集合组成，问X是否属于X？

抽象一些♿：$R=\{ X\mid X\notin X\}$

$如果R\in R，则不满足自己的条件，所以R\notin R$

$如果R\notin R，则又满足自己的条件，所以R\in R$

于是集合中的元素不能为集合本身🤓，否则就如上矛盾

$\LARGE{Ⅱ.亿点集合的小运算！}$

没想到吧，集合还有运算♿♿♿！

不过标题党害死人，集合只有3种运算🤓

$1.交集：集合\{ x|x\in A且x\in b\}称为A与B的交集，记为A\cap B.$

$2.并集：集合\{ x|x\in A或x\in b\}称为A与B的并集，记为A\cup B.$

$3.补集：\begin{cases}相对补集：集合\{ x|x\notin A且x\in B\}称为A在B中的相对补集，记作\complement_BA；\\绝对补集：集合A在全集U中的相对补集称为A的绝对补集，记作\complement_UA\end{cases}.$

主播主播，全集是啥🤔？就是给定的所有元素的集合♿

若看不懂，请看下图👇：

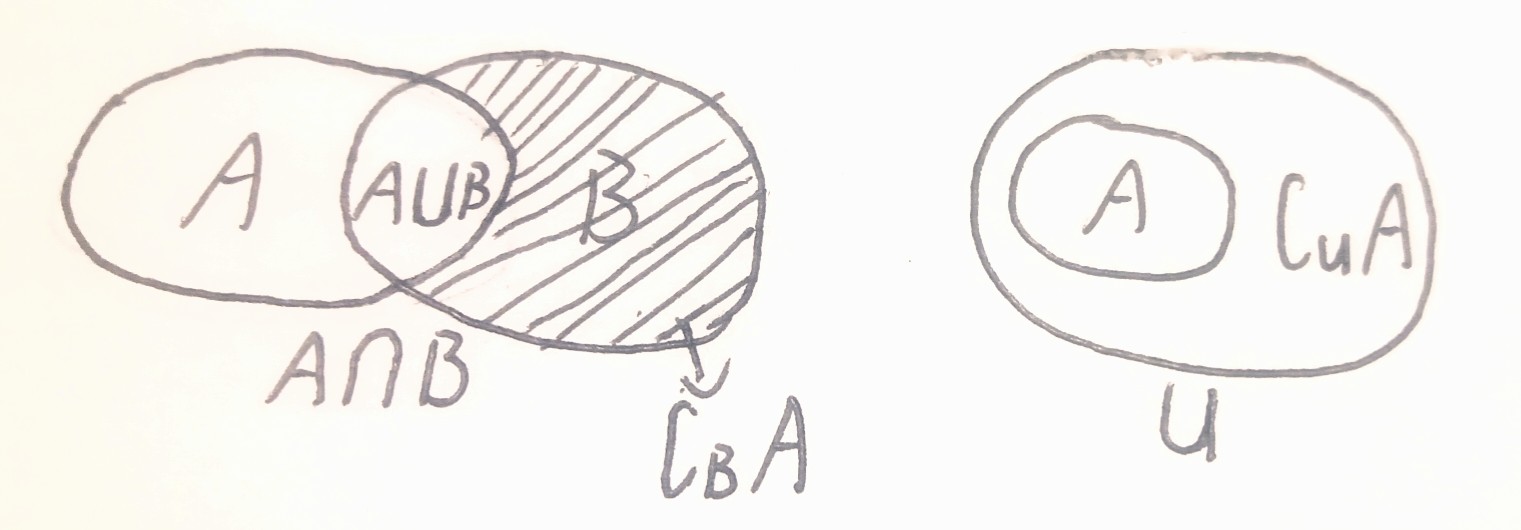
让我们来做点小练习吧🤓！

$\LARGE{习题1}$

$1.已知\{ a，\frac{b}{a}，1\} =\{ a^2，a+b，0\} ，则a^3-b^4=\underline{~~~~~}$.

未完待续......(如有错误，请指出，谢谢🤝🏻🤝🏻)