物理

[几何最值]浅谈胡不归模型

最近课内一直在学这东西，开个坑打算通过讲解来加深印象

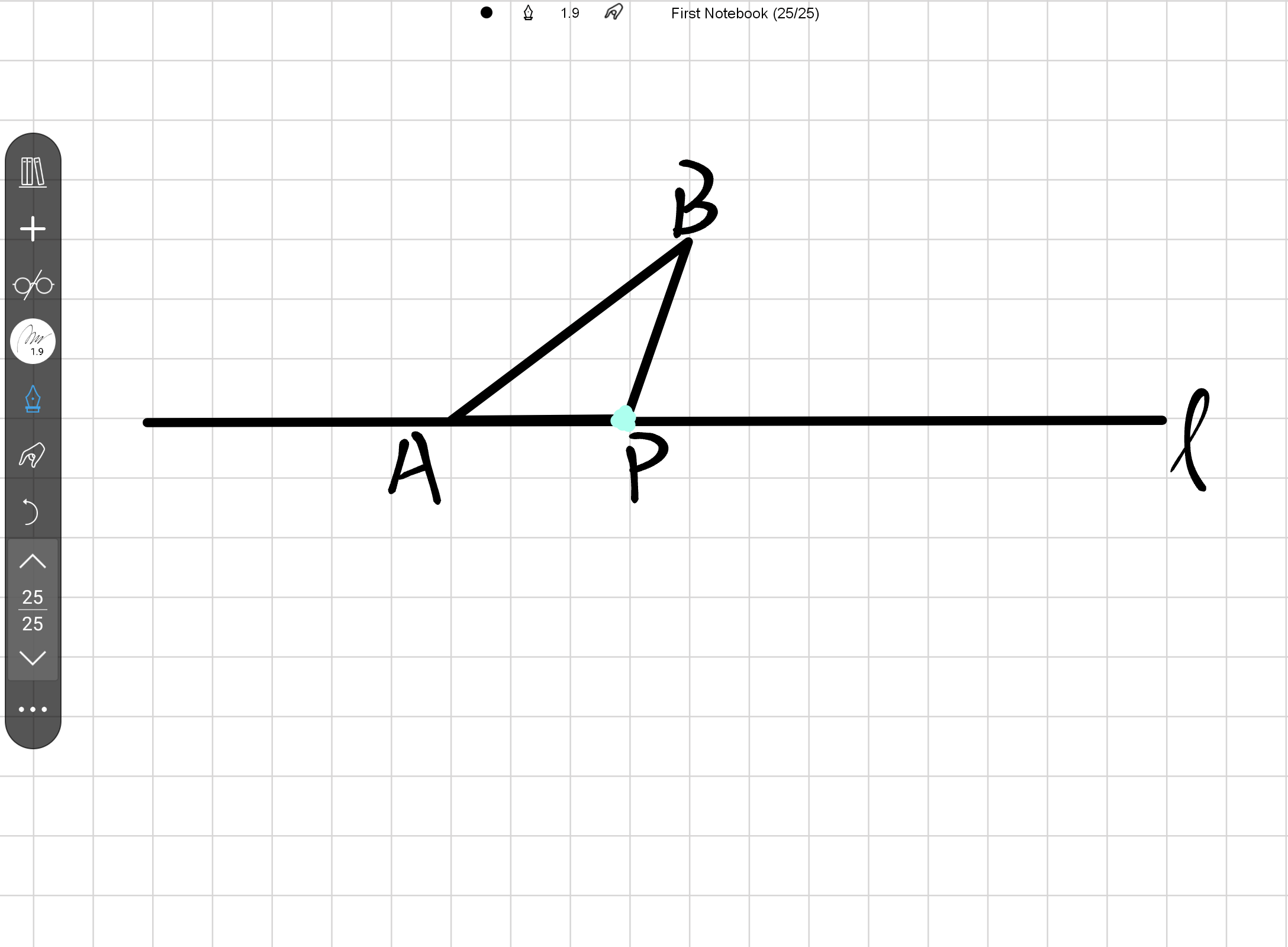
$$点A为直线l上一定点，点B为直线外一定点，点P在直线l上运动

$$问：如何确定点P，使得kAP+BP(0<k<1)最小？

抽象分析：这种带有系数的折线最值问题，通常我们会采用“化折为直”的办法

$$说正常点就是把折的变成直的（线段），再利用两点之间线段最短或者垂线段最短来解决

$$图中我们可以利用垂线段最短的性质，具体解题步骤如下：

$$一找：找到带有系数k的线段kAP

$$二构：在点B异侧，构造以线段AP为斜边的直角三角形

$$如图所示（ink绘图一直出问题😭）：

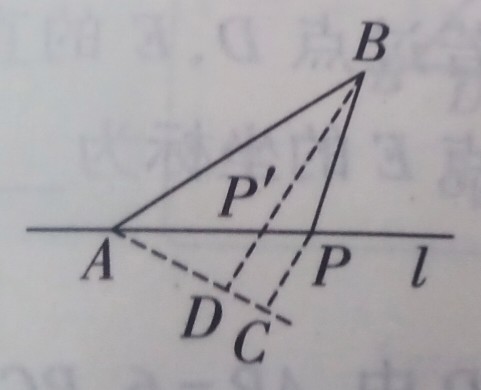
$$三转化：化折为直，$$将kAP转化为PC

$$四求解：$$使得kAP+BP=PC+BP，利用垂线段最短转化为求BD长度

$$例题：

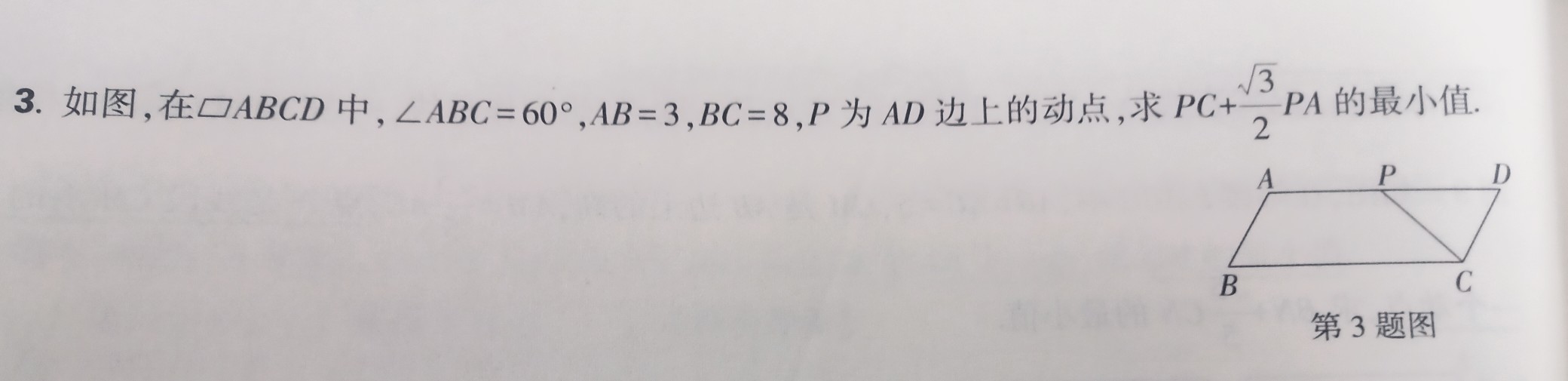
做法：