物理

分数量子霍尔效应

$\huge{已完结}$

建议先阅读上个帖😋

$\huge{引言}$

霍尔电阻不仅在强磁场下有整数变化的规律，还有分数变化的规律。分数量子霍尔效应可以说是打开了一个全新的领域，甚至可以说是把凝聚态物理的地位提升到了一个新的高度。分数量子霍尔效应意味着，我们可以通过凝聚态的量子系统去人为创造出一些自然界本不存在的物理学规律。

比如基本粒子在量子统计规律上分为两大类：玻色子、费米子。如果两个玻色子相互交换位置，它们整体的波函数会获得一个数值是 1 的相位，比方本来的波函数假设是$\phi(x, y)，x和y$ 分别是两个玻色子的坐标，然后把两个玻色子交换，变成了$\phi(y, x)$，两个玻色子的交换会告诉我们,    $\phi(x, y)=\phi(y, x)$，但如果是费米子的话，它会获得一个 -1 的相位，也就是 $\phi(x, y) =-\phi(x, y)$。

但是分数量子霍尔效应这个“分数”的意义在于，我们可以在量子系统中获得一些准粒子（quasi-particle），它们并非粒子物理当中那些真实存在的基本粒子，而是凝聚态物理系统中被激发起来的一些量子行为，这些行为像是量子粒子的行为。其实我们前文提到的“声子”也可以被认为是一种准粒子，它不是粒子物理意义上的基本粒子，而是一个量子系统在某种情况下表现得像粒子（act like a particle），这些准粒子是从凝聚态物理系统中“涌现”（emergent）出来的。准粒子的概念最早也是由朗道提出的。分数量子霍尔效应中的一些准粒子在量子统计规律上，它们既不是玻色子也不是费米子。交换这两个准粒子，它们的波函数获得的相位不是 1 也不是 -1 ，而是一个模是 1 的复数。这种统计规律叫分数统计（fractional statistics）。当然，它们只能存在于分数量子霍尔效应这样的二维量子多体系统中。这些既不像玻色子也不像费米子的准粒子也被称为任意子（anyon）。

这样的任意子，目前在自然界看来是不存在的，也就是说，粒子物理的实验中完全没有发现这样拥有分数统计的粒子，粒子物理中也没有针对分数统计的理论。这完全是分数量子霍尔效应当中产生的奇特现象。这其实是给我们的基础物理研究指出了一个新方向，就是除了用高能对撞机不断撞出更小的粒子以外，我们还可以尝试用人为构造的凝聚态系统，模拟一些最基本的物理原理，分数量子霍尔效应就是一个很好的例子。我们通过这个凝聚态系统甚至模拟出了自然界中本不存在的粒子物理规律。这同时也启发了我们，准粒子是从凝聚态系统中涌现出来的，那么粒子物理意义上的这些基本粒子，是不是也是某些更加基本的“凝聚”当中“涌现”出来的呢？也就是，时空未必只有时间和空间，基本粒子并非独立存在于时空当中，基本粒子也许只是一些更基本的“凝聚”系统中的“涌现”。由华人物理学家文小刚提出的“弦网凝聚”（string-net condensation）阐述的正是这种思想，弦网凝聚理论中，电子和光子都是从弦网中涌现出来的。

$\huge{Part 1.分数量子霍尔效应的发现}$

整数量子霍尔效应已经够令人吃惊了，但是，1982年Tsui和Stormer发现了更令人吃惊的事情，他们在低温和更强磁场下测量了霍尔电阻$ρ_{xy}$，结果发现，不仅在$\nu$等于整数的时候会出现量子化平台，而且在$\nu$为分数的时候也会出现量子化平台，如下图

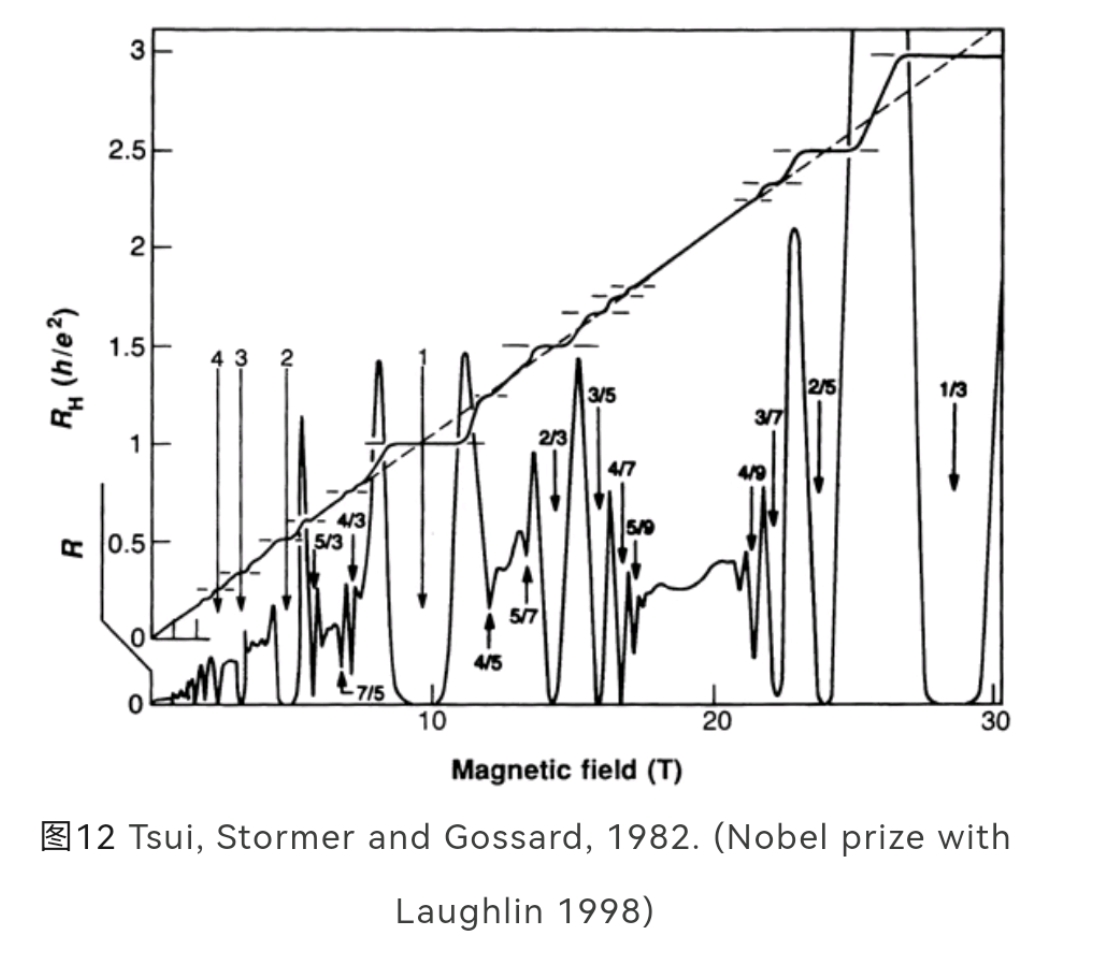
显然为了理解这种分数量子霍尔效应我们不能再忽略电子间的相互作用，否则的话前面我们理解整数量子霍尔效应时使用的单电子填充朗道能级就依然完全成立，那我们就只能得到整数量子霍尔效应。为了解释朗道能级部分填充时出现的分数量子化现象，电子间的库伦排斥力将非常重要，估算库伦排斥能$\frac{e^2}{4πε_0l_{b}}=\frac{\hbar\alpha_c}{l_B}$,会发现它和朗道能级$\hbarω_B$相差不大，所以某种意义上人们应该考虑为什么量子霍尔效应中的解释可以忽略电子间的库伦排斥力，所以分数量子霍尔效应的发现其实是使得人们开始意识到，单电子近似有时候是不成立的，电子间的相互作用可能非常重要，这就是所谓的强耦合强关联问题。

之所以量子霍尔效应可以忽略电子间相互作用，是因为重要的是讨论朗道能级被填满的情况，相互作用不会实质的改变物理图像，但对于分数量子霍尔效应，它的朗道能级是部分填充的，将会有巨量的不同填充方式，比如对于$\nu=\frac{1}{3}$的情况，这时候将$N=\frac{N_{\Phi}}{3}$的电子填充到最低朗道能级的$N_{\Phi}$个态中，填充方式将会有

$C^{\frac{N_{\Phi}}{3}}_{N_{\Phi}}=\frac{N_{\Phi}!}{(\frac{N_{\Phi}}{3})!(N_{\Phi}-\frac{N_{\Phi}}{3})!}$

填充数通常都非常大，而这些不同的填充方式都是简并的，对应于整个材料的简并量子态。

神奇的是，在分数量子霍尔效应的系统基态(整个材料的基态)之上，可以出现奇异的准粒子激发，所谓准粒子意思就是不是自然界中普遍存在的粒子，因此不是组成霍尔片材料本身的电子和离子，而是在霍尔片中出现的行为和一个粒子的行为完全类似的一种局部状态。它们本质上是分数量子霍尔效应中的电子通过相互作用产生的东西，但是分数量子霍尔效应中出现的这些准粒子非常奇怪，它们可以有分数电荷！比方说在$\nu=1/3$的霍尔态中可以出现$e/3$电荷的准粒子激发，而且根据上文，我们可以知道自然界中的粒子可以分为玻色子和费米子，而在引言中我们提到了这些粒子被称为任意子。而且我们知道电子可以有两种不同的自旋状态自旋向上和自旋向下，它们是电子的内禀状态，但是在某些分数量子霍尔效应中出现的准粒子甚至可以有诸如$\sqrt{2}$这样无理数个不同的内禀状态！

$\huge{Part.2基态波函数———Laughlin函数}$

根据任意基态的表示方式$\Psi_0,m∼w^me^{-\frac{|w|^2}{4l^2_B}}$

电子最低朗道能级$(\nu=1)$的单粒子态为$u_i(w,\overline{w})=w^ie^{-\frac{|w|^2}{4l^2_B}}$

式中$w=x+iy为二维平面的复坐标。这样的2+1维电子系统满足全同费米统计，因此对于填满最低朗道能级的\N_{\Phi}=\frac{eBS}{2π\hbar}$个电子而言，它们的多体波函数必须是一个全反对称波函数，填充方式唯一。因此波函数也是唯一的，由下面的行列式给出

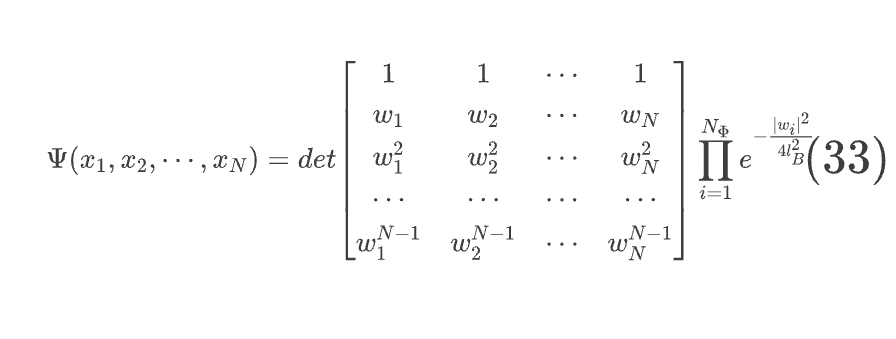
其中的行列式是范德蒙行列式，利用其标准计算结果，多体波函数表达为

$\Psi=(x_1,x_2,\cdots,x_N)=\prod_{1≤i≤j≤N_{\Phi}}(w_i-w_j)\prod^{N_{\Phi}}_{I=1}e^{-\frac{|w|^2}{4l^2_B}}$

Laughlin正是通过推广这个整数量子霍尔效应波函数，从而给出了分数量子霍尔效应的一个理论解释。

起初人们不觉得这个波函数有多大的重要性，然而laughlin用他的神来之笔将这个波函数作了一点“简单”推广就成了人们理解分数量子霍尔效应的基础。Laughlin指出对于$\nu=1/m，m$是一个奇数的分数量子霍尔效应，其基态的试探波函数可以取成如下形式

$\Psi(\mathrm{x})^{(m)}=\prod_{1≤i≤j≤N_{\Phi}}(w_i-w_j)\prod^{N_{\Phi}}_{I=1}e^{-\frac{|w|^2}{4l^2_B}}$

这就是著名的Laughlin波函数，式中电子数目$N_{\Phi}=m(N-1)$

从而，$N$很大的时候填充分数$\nu=N/N_{\Phi}\rightarrow\frac{1}{m}$。之所以有$N_{\Phi}=m(N-1)$是因为$m(N-1)$是Laughlin波函数全纯多项式部分的最高次幂，这个最高次幂(角动量量子数m)决定了霍尔液滴的半径$r_m\sqrt{2m}l_B，两个相邻量子数m$的霍尔液滴之间的面积差是$2πl^2_B$，对于一个磁通量子。所以这个幂次本身应该等于朗道能级的总磁通量子数$N_{\Phi}$。正因为电子数目公式的成立有自然的理由，所以我们反过来知道，Laughlin波函数的确解释了填充分数$\nu=1/m$。

$\huge{Part3.等离子体类比}$

Laughlin波函数是一个看起来不错的分数量子霍尔效应的试探波函数，下一步是利用这个多体波函数来计算各种物理量的期望值，但由于$N$数目太大，这不容易下面简要看一种处理这一问题的统计物理方法。

假设我们想要计算出量子霍尔液滴的平均密度，我们需要计算密度算子的期望值

$n(z)=\sum^N_iδ(w-w_i)$

对波函数无量纲化为

$\Psi^{(m)}_L=\prod_{i小于j}\frac {(w_i-w_j)^m}{l^m_B}e^{-\sum{}_i\frac{|w_i|^2}{4l^2_B}}$(PS：请自己在ij之间加一个<，我这里加了会乱码)··········(a)

计算归一化给出：

$n(z)=\sum^N_iδ(w-w_i)=\frac{∫Π^N_{i=1}d^2w_in(z)P[w_i]}{Π^N_{i=1}d^2w_inP[w_i]}$············(b)

此处引入了与Laughlin波函数相关的非归一化概率密度

$P[w_i]=\prod_{i小于j}\frac {(w_i-w_j)^m}{l^m_B}e^{-\sum{}_i\frac{|w_i|^2}{4l^2_B}}$(同式a)

积分很难，如何进行呢？

重要的观察是，期望值(a)具有与我们在经典统计力学中计算的类型相同的形式结构，其中分母解释为配分函数。

$Z=\prod^N_{i=1}d^2w_iP[w_i]$

实际上可以把概率分布(b)写成玻尔兹曼分布函数，

$P[w_i]=e^{-βU[w_i]}$

$βU[w_i]=-2m\sum_{i小于j}log\left(\frac{|w_i-w_j|}{l_B}\right)+\frac{1}{2l_B^2}\sum^N_{i=1}|w_i|^2$

为了看出这个统计物理系统到底是什么系统，我们进一步将逆温度$β$取成如下形式

$β=\frac{2}{m}$

那么这个统计物理系统的相互作用能$U[w]$就应取成

$U[w]=-m^2\sum_{i小于j}log\left(\frac{|w_i-w_j|}{l_B}\right)+\frac{m}{4l_B^2}\sum^N_{I=1}|w_i|^2$

'这刚好是N个“电荷”$q=m$的带电粒子在一个背景负“电荷”上的等离子体势能。也即是说，计算Laughlin波函数的归一化以及物理量期望值的问题，等价于一个逆温度$β=2/m$的二维等离子体系统的统计物理问题，所以我们把这种方法称作等离子体类比。

理解它有两个关键，首先要看第一项，它描述的是两维平面内多个电荷为$q=m$的带电粒子之间的库伦相互作用势能。为了理解这一点，请注意二维泊松方程告诉我们，点电荷q产生的静电势$\phi$为

$-\nabla^2\phi=2πqδ^2(\mathbf{r})\Rightarrow\phi=-qlog\left(\frac{r}{l_B}\right)$

注意到两个点电荷之间的电势能$U=qphi$我们容易知道$U[w]$的第一项确实是两维带电粒子系统的相互作用电势能。

第二项描述的是一个恒定电荷背景下的中和环境。一个恒定的电荷密度$ρ_0$背景将会产生服从于$- abla^2phi=2πρ_0$的静电电势，第二项服从

$- \nabla^2\left(\frac{|w_i|^2}{4l_B^2}\right)=-\frac{1}{l^2_B}$

它告诉我们每一个电子感受到一个背景电荷密度

$ρ_0=-\frac{1}{2πl_B^2}$

背景负电荷密度$ρ_0$的大小正好是磁通量子的密度。

现在我们可以用这幅等离子图像帮助我们思考了。为了使能量最小化，平均而言，等离子体想要中和背景电荷密度。每个粒子带电荷$q=m$，这意味着粒子密度n但补偿密度应为$nm+ρ_0=0$，或

$n=\frac{1}{2πl_B^2}\frac{1}{m}$

这刚好是填充分数$ u=1/m$的分数量子霍尔系统的电子数密度。这是因为，等离子体类比中的$q=m$带电粒子正好相应于原来Laughlin波函数中的电子。所以我们这里实际上是利用等离子体类比得到了正确的填充分数

$\huge{Part.4准粒子激发—分数电荷}$

分数量子霍尔效应的神奇之处之一是，它有一些带分数电荷的准粒子激发。实际上，有两种不同电荷符号的准粒子激发，分别称作准空穴和准电子。准空穴带正电，准电子带负电。下面讨论如何利用Laughlin波函数描述这些准粒子激发。

4.1准空穴(Quasiholes)

描述一个位于复坐标 $(\eta) $的准空穴的波函数$\Psi_{qh}(w; \eta)$为

$\Psi_{qh}(w;\eta)=\prod^N_{I=1}(w_i-\eta)\Psi^{(m)}_L(w)}$

式中$\Psi_L^{(m)}(w)$就是刚才给出的Laughlin波函数。从这个波函数我们很容易看出，电子在$\eta$位置出现的概率密度为0。也就是说，我们在原来的多电子形成的液体中创生了一个空穴，所以称之为准空穴。

准空穴的奇异性质之一是，它携带$e^* = e/m$的分数电荷。注意，电子携带的是$-e$的电荷，因此准空穴携带的是正电荷。值得注意的是，在这个描述中，准空穴是系统在$\eta$位置的一个缺陷，因此$\eta$本身并不是动力学变量，而是准空穴波函数的一个参数，动力学变量是电子的坐标$w_i$。

为了解释为什么准空穴的电荷是$e/m$，我们不妨在$\eta$位置放$m$个相同的准空穴，描述这$m$个准空穴的波函数当然应该是

$\prod_{i=1}^{N} (w_i - \eta)^m \Psi_L^{(m)}(w) $

很明显的是，如果$\eta$是一个动力学变量，那这个波函数就是标准的Laughlin波函数，只不过位置也有一个电子。但现在$\eta$不是动力学变量，而只是一个参数，因此$\eta$位置的这个电子实际上是缺失的。也即是说$\eta$位置的$m$个准空穴等价于$\eta$位置的一个电子缺失，因此一个准空穴就相当于$1/m$个电子缺失。由于电子带$-e$的电荷，电子缺失就相当于$+e$的正电荷，因此一个准空穴就相当于一个$e/m$的正电荷。

将这个描述推广到$M$个准空穴，相应的波函数是

$\Psi_{qh}(w; \eta_1, \eta_2, \cdots, \eta_M) = \prod_{\alpha=1}^{M} \prod_{i=1}^{N}(w_i - \eta_\alpha)\Psi_L^{(m)}(w)$

4.2准电子(Quasielectrons)

与准空穴相反，准电子是一种携带负分数电荷的准粒子，其电荷为$-e/m$。写出准电子的试探波函数相对更难一些。

首先，我们注意到准空穴的存在会增加多电子波函数全纯多项式部分的幂次，从而扩大了霍尔液滴所占的总面积，降低了液滴的密度。这是因为空穴的存在将电子排挤到了更远一点的地方。而准电子则相反，它相当于在霍尔液滴上多鼓出了一个小包，因此准电子的存在会升高液滴的密度，从而也就需要缩小霍尔液滴所占的面积，这就意味着准电子的存在应该降低波函数全纯多项式部分的幂次。如果我们想减小角动量，我们不允许除以              $Π_iw_i$，因为得到的波函数非常奇异。我们也不能乘以$Π_i\bar{w}_i$，因为尽管这会降低角动量，但得到的波函数不再位于最低朗道能级。相反，降低多项式次数的一个简单方法是做微分。基于此，Laughlin猜测一个位于坐标原点的准电子将有如下波函数

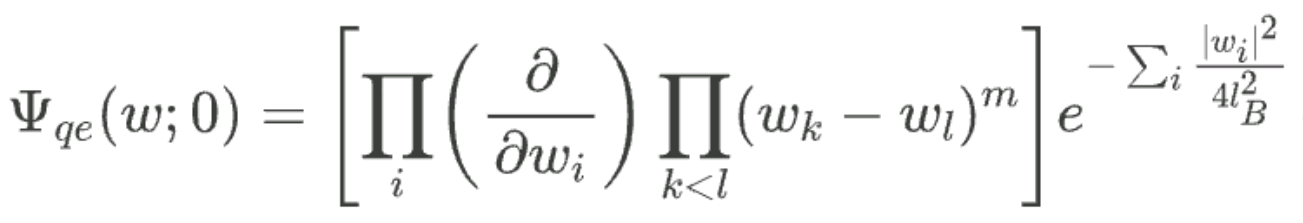
很显然，偏导项的存在正确地将每一个$w_i$的幂次降低了1，从也就将每一个电子的角动量量子数降低了1，因此每一个电子都会朝原点挪动一个轨道，由于所有的单电子轨道中，实际被电子占据的只有$\nu = 1/m$，所以总的来说，原点处就会累积出$ -\nu e = -e/m$的电荷，这就是原点处的准电子的电荷。

如果准电子不是位于坐标原点，而是位于复坐标$\eta$处，注意到轨道角动量量子数的吻合，人们应该将准电子波函数写成

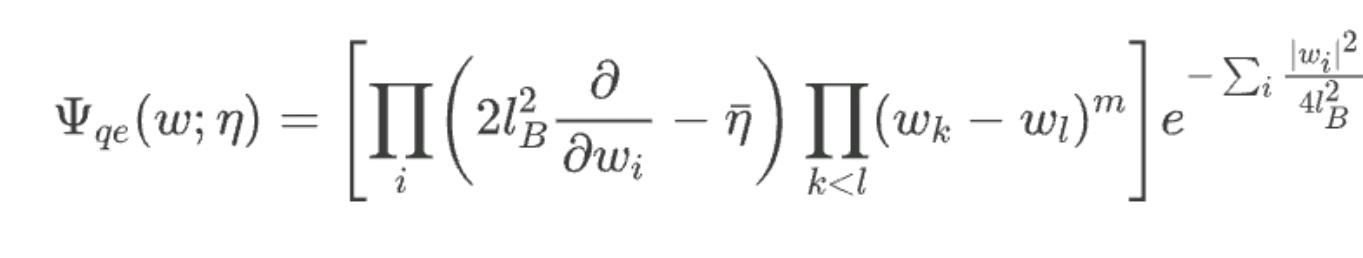
式中$\bar{\eta}$是$\eta$的复共轭，式中偏导前面的因子$2l_B^2$来自于$\bar{w}_i$的朗道能级正好是$2l_B^2 \partial/\partial w_i$。