物理

一道物理题

应该是1/2吧……

我是新人如果做错了请原谅😥

这是即答给出的回答：

为了求解 \(\frac{t_1}{t_2}\) 的值，我们首先需要逐步分析题目中给出的信息。

### 1. 理解初始条件

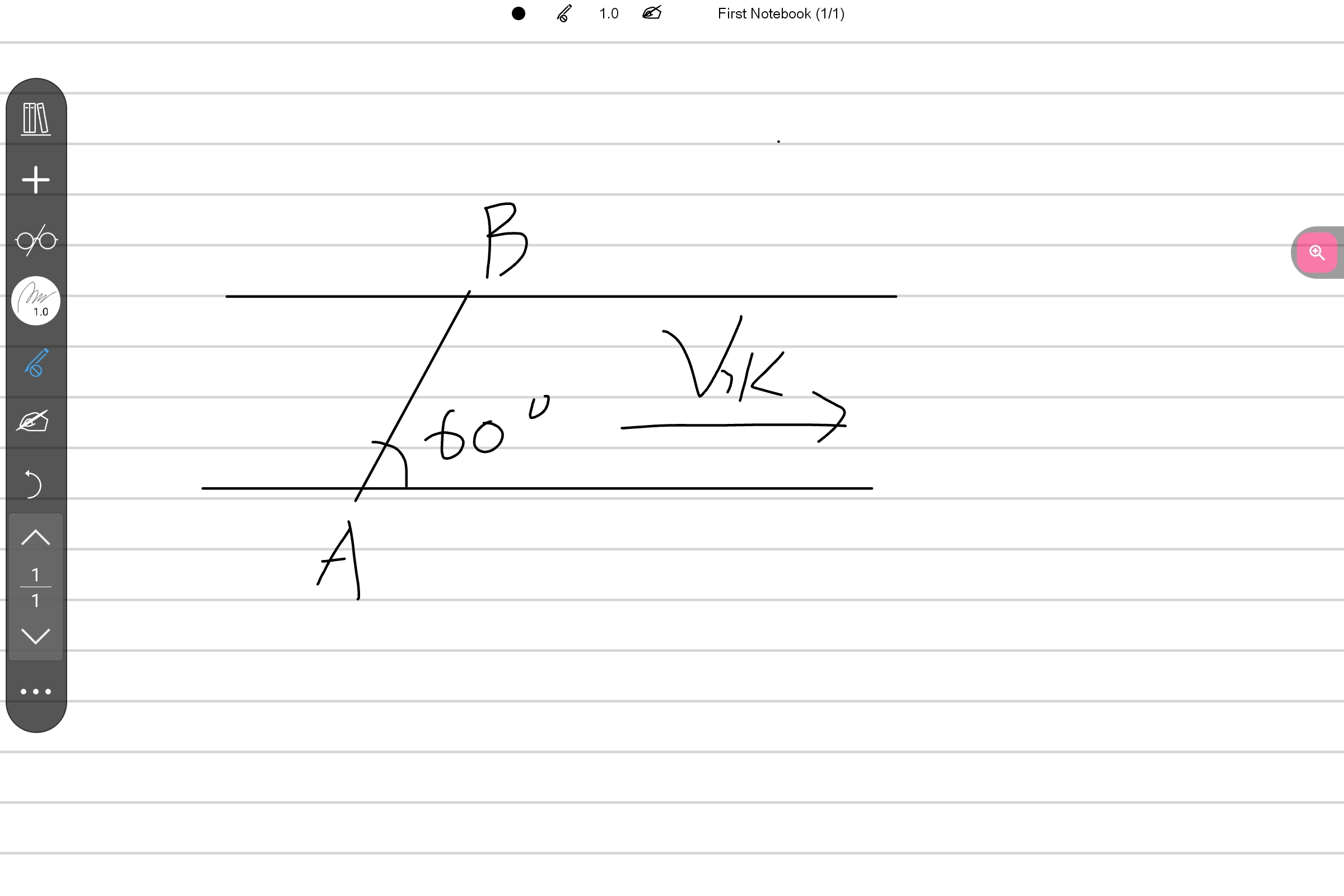
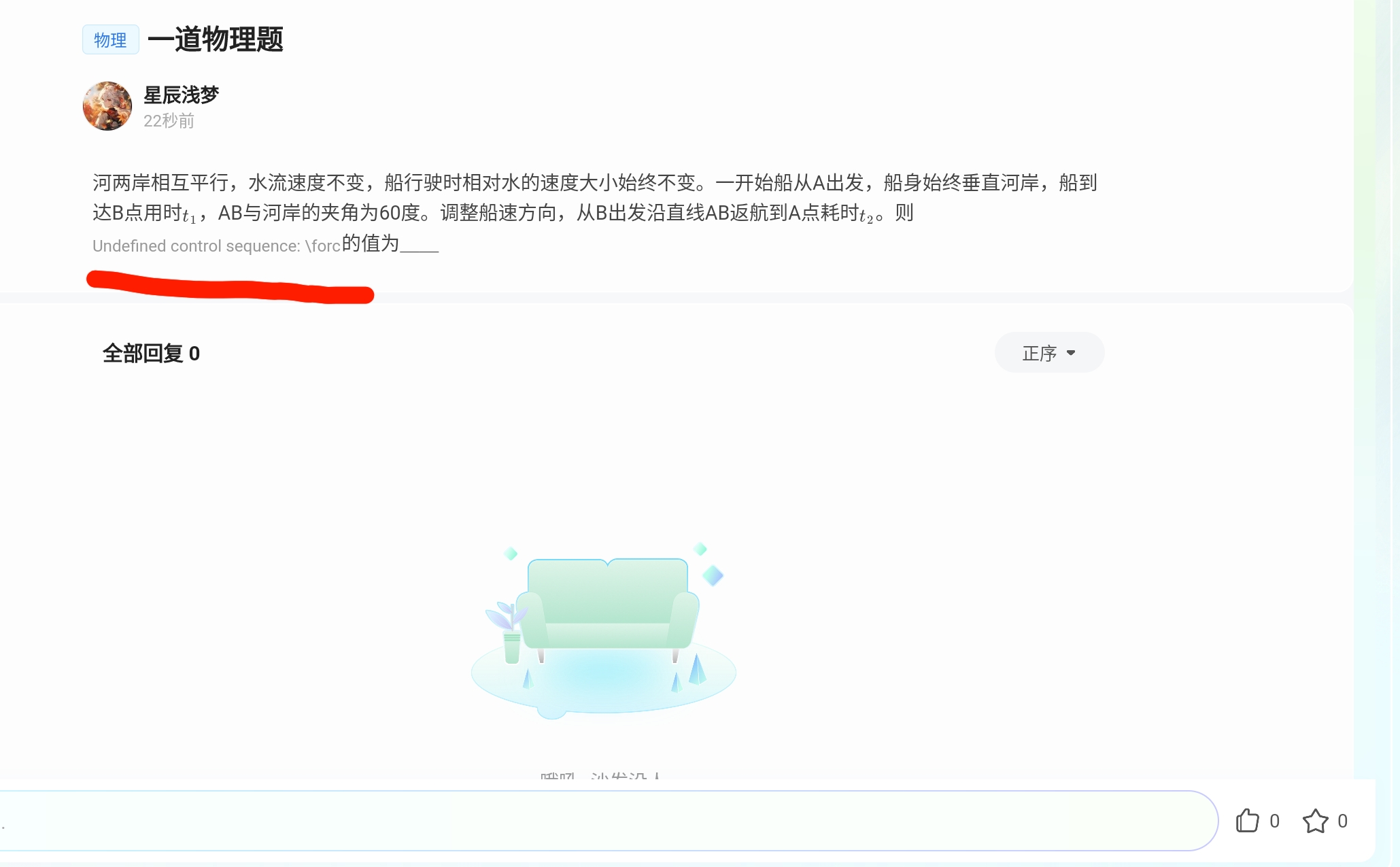
- **河两岸相互平行，水流速度不变，船行驶时相对水的速度大小始终不变。**

- **船从A出发，船身始终垂直河岸，船到达B点用时 \(t_1\)，AB与河岸的夹角为60度。**

### 2. 确定船速和水流速

设：

- 船在静水中的速度为 \(v_c\)，

- 水流速度为 \(v_w\)，

- 河宽为 \(d\)（即A到对岸的垂直距离）。

### 3. 船从A到B的运动分析

- **船身始终垂直河岸**，即船的初始速度方向垂直于河岸，因此，船相对于水的水平分速度为0，垂直分速度为 \(v_c\)。

- **船到达B点用时 \(t_1\)**，则有 \(t_1 = \frac{d}{v_c}\)。

- **AB与河岸的夹角为60度**，这意味着船的实际位移（即AB段）在水平方向上的分量为 \(d \tan(60^\circ) = d\sqrt{3}\)。

- **船在水平方向上的实际速度** 为 \(v_w\)（因为船身垂直河岸，水平速度完全由水流提供），因此，船在水平方向上的位移为 \(v_w t_1 = d\sqrt{3}\)，即：

  \[

  v_w t_1 = d\sqrt{3} \implies v_w \cdot \frac{d}{v_c} = d\sqrt{3} \implies v_w = v_c \sqrt{3}

  \]

### 4. 船从B返回A的运动分析

- **调整船速方向，从B出发沿直线AB返航到A点耗时 \(t_2\)**。

- **船沿直线AB返航**，即船的实际速度方向沿AB线，设船在静水中的速度 \(v_c\) 与AB线的夹角为 \(\theta\)，则：

  \[

  \cos(\theta) = \frac{v_c \cos(\theta)}{\sqrt{(v_c \cos(\theta))^2 + (v_w - v_c \sin(\theta))^2}} = \cos(60^\circ) = \frac{1}{2}

  \]

  这意味着：

  \[

  v_c \cos(\theta) = \frac{v_c}{2}

  \]

  因此：

  \[

  v_c \sin(\theta) = \sqrt{v_c^2 - \left(\frac{v_c}{2}\right)^2} = \sqrt{\frac{4v_c^2 - v_c^2}{4}} = \sqrt{\frac{3v_c^2}{4}} = \frac{\sqrt{3}v_c}{2}

  \]

- **船沿AB线的实际速度** \(v_{\text{actual}}\) 为：

  \[

  v_{\text{actual}} = \sqrt{\left(v_c \cos(\theta)\right)^2 + \left(v_w - v_c \sin(\theta)\right)^2} = \sqrt{\left(\frac{v_c}{2}\right)^2 + \left(v_c\sqrt{3} - \frac{\sqrt{3}v_c}{2}\right)^2} = \sqrt{\left(\frac{v_c}{2}\right)^2 + \left(\frac{2\sqrt{3}v_c}{2} - \frac{\sqrt{3}v_c}{2}\right)^2} = \sqrt{\left(\frac{v_c}{2}\right)^2 + \left(\frac{\sqrt{3}v_c}{2}\right)^2} = \sqrt{\frac{v_c^2}{4} + \frac{3v_c^2}{4}} = \sqrt{\frac{v_c^2 + 3v_c^2}{4}} = \sqrt{\frac{4v_c^2}{4}} = v_c

  \]

- **船从B返回A的 时间 \(t_2\)** 为：

  \[

  t_2 = \frac{\text{distance AB}}{v_{\text{actual}}} = \frac{\text{distance AB}}{v_c}

  \]

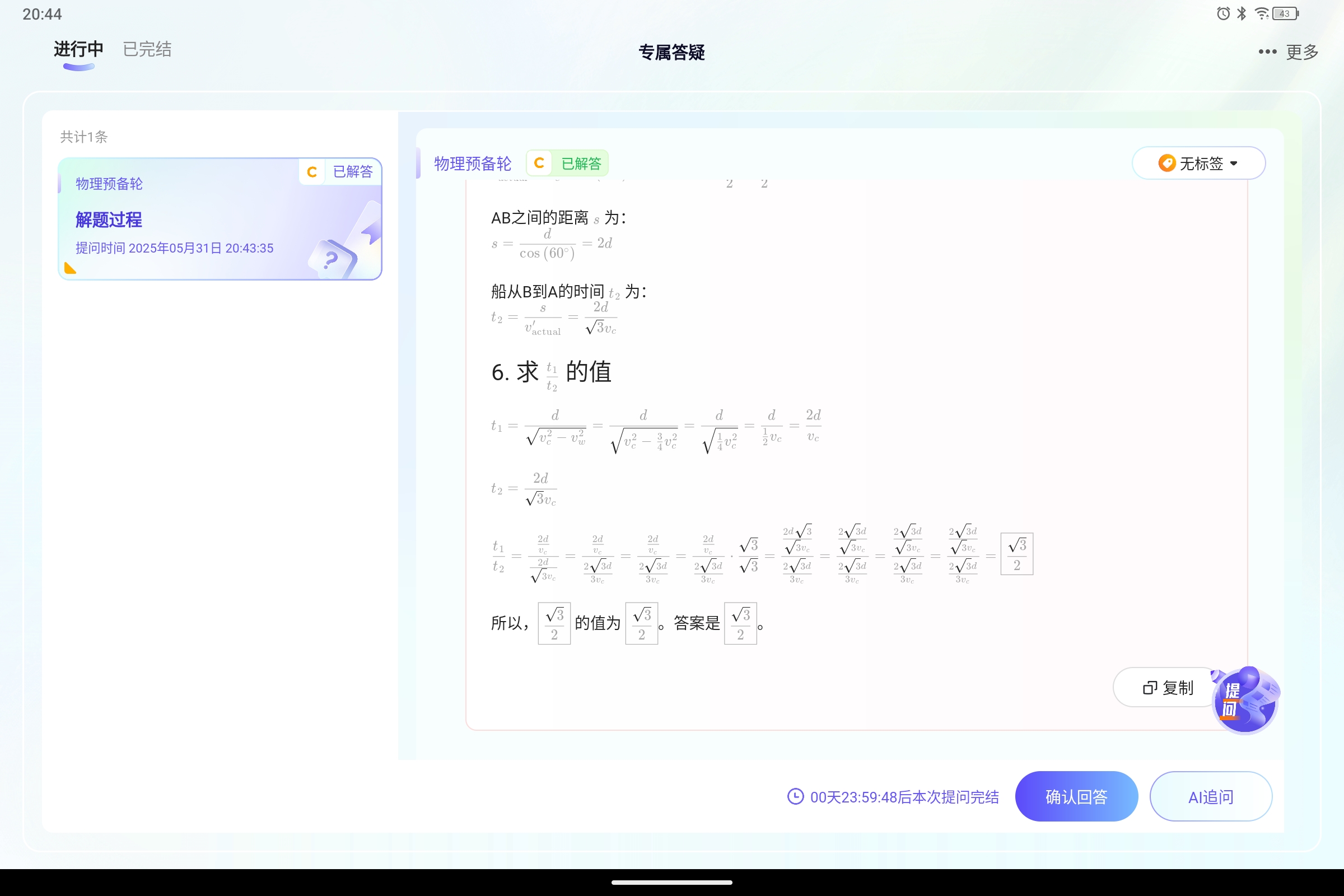
  而 \(\text{distance AB} = \frac{d}{\cos(60^\circ)} = \frac{d}{\frac{1}{2}} = 2d\)，因此：

  \[

  t_2 = \frac{2d}{v_c}

  \]

### 5. 求 \(\frac{t_1}{t_2}\) 的值

- \(t_1 = \frac{d}{v_c}\)

- \(t_2 = \frac{2d}{v_c}\)

因此：

\[

\frac{t_1}{t_2} = \frac{\frac{d}{v_c}}{\frac{2d}{v_c}} = \frac{\frac{d}{v_c}}{\frac{2d}{v_c}} = \frac{d}{v_c} \cdot \frac{v_c}{2d} = \frac{1}{2}

\]

所以，\(\boxed{\frac{1}{2}}\) 是最终答案。答案是 \(\boxed{\frac{1}{2}}\)。