物理

量子霍尔效应

第一个学术帖，$\huge{完结辣！！！}$

给大家推荐一本适合物竞未入门的人读的一本书，也是本帖知识来源之一，叫六极物理，对数学基础零要求，初中生都能看懂，介绍了许多近代物理的内容

量子霍尔效应是我在一本书上看到的，经过一些资料查阅和整理，最终整理出以下内容

$\huge{1.霍尔效应}$

霍尔效应在1879年由美国物理学家霍尔发现，其内容为：一块厚度为$h$宽度为$d$的导体板放在垂直于它的磁感应强度为$B$的磁场中，当有大小为$I$的电流通过时，在导体板的上下侧面会产生大小为$U=k\frac{IB}{d}$的电势差

原理：电流通过时，磁场使得通过的电子受洛伦兹力聚集在导体板的一侧，在另一侧会出现正电荷，从而形成电场，电场对电子施加与洛伦兹力方向相反的电场力，当两个力相互平衡后即$B=\frac{U}{hv}$时,上下两侧会形成稳定的电势差

同时，在此处我们定义一个量霍尔电阻，它等于霍尔电压大小比上通过的电流的大小

$\huge{Part.2量子霍尔效应}$

在20世纪七十年代科学家们发现了量子霍尔效应，根据定义霍尔电阻$R_{H}=\frac{U}{I}=\frac{kB}{d}$,很显然，$R_{H}$与B是成正比的，画出来的图像应该是线性的，可是实际上当磁场达到10T以上，温度只有1K时，画出来的图像是一个阶梯状的图像，如下图

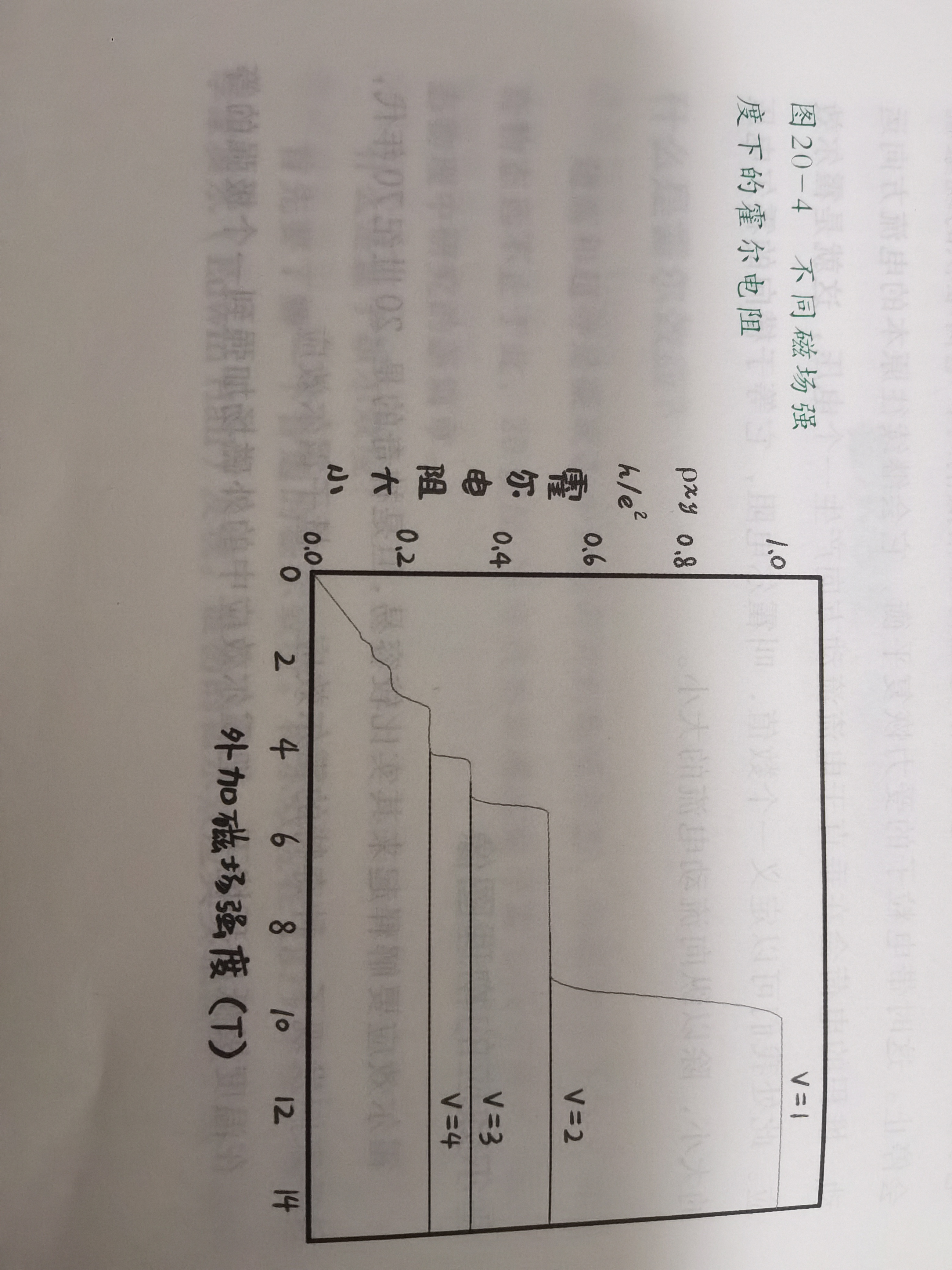
也就是说，随着外加磁场的变化，当磁场很强的时候，霍尔电阻在一定范围内都是一个精确的恒定值，这每一个台阶，其实都可以写成

$R_{H}=\frac{h}{e^2 u}$的形式，其中$\nu$叫填充因子(filling factor)($\nu=1,2,3,4……$可取任意正整数)

当我们看到离散时就想到量子化，并且这个电阻里还有普朗克常数，说明与量子力学有关，极低温下，正是多粒子系统量子力学效果占据优势的时候

当磁场比较弱的时候，洛伦兹力比较小，电子做圆周运动的半径较大，无法产生大的偏转，可当磁场比较强的时候，电子半径就会减小，甚至原地转圈，如图

在这种情况下，金属板想要导电就没有那么容易了，在金属板内部的电子都在原地转圈，就没法在电路中形成电流。但在边缘的电子还是可以形成电流的。对于边缘的电子，我们假设它与金属板边是是弹性碰撞，正面碰上去后会原速反弹继续形成一个新的半圆转下去，再正碰，再反弹，如此往复，所以在磁场极强的情况下，只有边缘的电子可以参与导电

对于这些电子，我们显然不能再用经典的电磁学去描述这些电子的运动，而是应该用薛定谔方程来描述它们的量子行为，我们知道，电子的能量有两部分，一部分是电子的动能，一部分是电子的电势能，对于量子霍尔效应也一样，这个金属板里的电子有动能，并且由于金属板里的电子是自由子，所以电子的势能只需要考虑外磁场的势能，这样就可以求解电子的薛定谔方程了，那么很自然的，可以猜想这跟原子里的电子轨道一样，量子霍尔效应里解出来的量子化的能级，叫做朗道能级，接下来是推导

$考虑二维平面上质量为m电荷量为e的电子$，处在沿$z方向的匀强磁场\mathbf{B}=B\hat{z}$中，考虑对称规范$\mathbf{A}=\frac{B}{2}(-y,x,0)$，

根据正则动量$\mathbf{p}与机械动量\mathbf{k}的关系\mathbf{p}=\mathbf{k}+\frac{e}{c}\mathbf{A}(这里取c=1自然单位制)$

那么电子的哈密顿量$H=\frac{1}{2m}\left[(p_x+\frac{eBy}{2})^2+(p_y-\frac{eBx}{2})^2\right]$

并定义产生算符$a^{\dagger}=\frac{1}{\sqrt{2}}\left(\frac{∂}{∂u}-u\right)和湮灭算符a=\frac{1}{\sqrt{2}}\left(\frac{∂}{∂u}+u\right)$

经过一系列数学变换，可将哈密顿量改写为$H=\hbarω_c\left(a^{\dagger}a+\frac{1}{2}\right),其中ω_c=\frac{eB}{m}为回旋频率$

根据量子力学中的对易关系$[a^{\dagger},a]=1,可以求解上述哈密顿量的本征值。因为a^{\dagger}a的本征值是n(n=0,1,2,3....)$

所以能量本征值$E_n=\hbarω_c\left(n+\frac{1}{2}\right)这就是朗道能级，每个朗道能级的简并度$

$N=\frac{eB}{\hbar}\frac{L_{x}L_{y}}{(2π)^2},其中L_x，L_y是二维系统在xy方向上的二维尺寸,设填充因子\nu=\frac{N_e}{N}$

霍尔电导量子化的推导

①Laughlin 的规范论证

Laughlin考虑了一个环形（或圆柱形）的二维电子系统，轴向施加均匀磁场。假设在环的中心引入随时间缓慢变化的磁通量$\Phi(t)$，其变化率产生环绕环的电场。根据法拉第定律，电场驱动电流，霍尔电导$σ_{xy}$可通过电流响应与磁通变化的比值确定,当磁通$\Phi(t)$变化一个量子单位

$\Phi_0=\frac{h}{e}$(磁通量子)时，系统的哈密顿量经历规范变换。波函数的周期性边界条件要求，此时波函数最多累积一个整体相位（单值性条件），系统回到原物理态。这一过程不改变物理可观测量，但导致电子在环的横向（径向）移动磁通变化$\Phi_0驱动霍尔电流，导致电荷Q$从环的一侧转移到另一侧。电荷转移量$Q与霍尔电导σ_{xy}$的关系为：

$Q=σ_{xy}·\Phi_0=σ_{xy}·\frac{h}{e},$由于电荷必须量子化为电子电荷的整数倍($Q=e\nu,\nu为整数$),联立方程得：$σ_{xy}=\nu·\frac{e^2}{h}$

直接导出霍尔电导的量子化

②Kubo公式计算霍尔电导

1.线性响应理论框架

$假设系统处于平衡态，受到弱均匀电场\mathbf{E}的扰动，电场通过矢势\mathbf{A}(t)=-\mathbf{E}t引入，微扰哈密顿量为：$

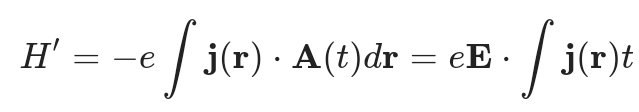
其中$j(r)$是电流密度算符

根据线性响应理论，电流的期望值$〈J_{\alpha}〉$可表示为：

$〈J_{\alpha}〉=σ_{\alpha\beta}E_{\beta}$

其中电导率张量$σ_{αβ}$由kubo公式给出：

$σ_{αβ}(ω)=\frac{1}{iω}[\Pi_{αβ}(ω+i0^{+})-\Pi_{αβ}(0)]$

这里$\Pi_{αβ}是电流—电流关联函数的松原函数，解析延拓后得到直流电导(ω\rightarrow0):

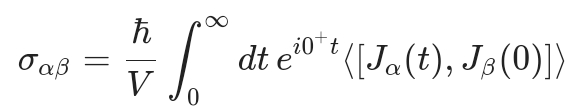
$其中V是系统体积，$J_{α}=\int~j_{α}(r)dr$,为总电流算符

霍尔电导对应横向响应$σ_{xy},在直流极直流极限(ω\rightarrow0)$下，公式简化为

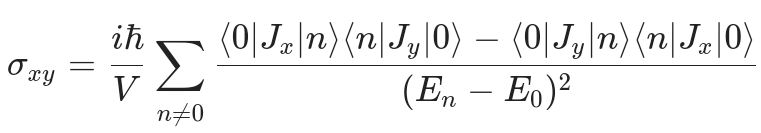
其中$|0\rangle为基态，|n\rangle为激发态，E_n为对应能量。$

在整数量子霍尔效应中，系统处于强磁场下的朗道能级填充态，基态为完全填充的能带，此时激发态与基态间有能隙$Δ$，低温下仅基态贡献主导，并且此时霍尔电导可表达为陈数(Chern number):

$σ_{xy}=\frac{e^2}{h}·C,C=\frac{1}{2π}\int_{BZ}Ω_{xy}(\mathbf{k})d^2k$

其中$Ω_{xy}(\mathbf{k})$是贝里曲率，积分覆盖整个布里渊区(BZ)，陈数C为整数，直接导致了霍尔电导的量子化

③两种论证的联系

kubo公式中的陈数与Laughlin中的磁通量子化均反映了系统的拓扑不变性，同时均导出了相同的霍尔电导

那么我们要怎么利用朗道能级来解释量子霍尔效应呢？

霍尔电阻就是横向电压比电流，我们知道电流只与边缘电子的运动状态有关，横向电压只与金属板边缘电荷数量有关，两个密度之比其实就决定了霍尔电阻的大小，在磁场变化的条件下，如果电荷密度与电流的电子密度之比是一个恒定不变的值这样就可以解释为什么霍尔电阻在提升磁场的情况下是一个恒定不变的值了

通过上述推导可以发现，电子不同的能量等级对应了不同的朗道能级，它的排布是从低能量开始，填满了低能量的朗道能级，才会再填高能量的朗道能级。

再来看单个朗道能级的特点，每个朗道能级中电子所处的状态只有转圈或转半圈。定义一个物理量$N_{Φ}$，它是单位面积中能够存在的一个朗道能级所对应的电子转圈的个数。那么可以知道外磁场越强，朗道能级的圆圈的面积就越小，$N_{Φ}就越大，再引入物理量电荷密度N_e$,，填充因子就是二者之比。

我们现在来看一个朗道能级对应的圆圈所占据的面积当中，有多少电子，单个朗道能级所占面积中的电子数实际上就是填充因子$\nu$。我们论证，外磁场越大,$\nu$就越小，则导电性越差，霍尔电阻就越大。当外部磁场增强的时候，单个朗道能级对应的圆圈面积就越小，单位面积中的朗道能级数量就越多，因此$N_{Φ}$就越大，根据填充因子$\nu$的定义,$\nu$越小。朗道能级的圆圈面积越小，这块面积当中存在的电子数就越少，因此在边缘上，能够参与导电的电子数就越少，参与导电的电子数越少就说明电流越小，电流越小则说明霍尔电阻越大。因此我们就论证了，即便在量子霍尔效应的情况下，增大外磁场也会使得霍尔电阻变大。

电阻的阶梯状又应该怎么解释呢？这里的关键是，正常情况下导体金属板不可能没有任何杂质，这种杂质体现为系统中的无序（disorder）效果，电子的运动状态是局域化地集中在紊乱地区附近的，它们都不参与导电，在外磁场强度变化比较小的过程中，这些局部的紊乱无法被破坏，因此在外磁场强度变化不大时，霍尔电阻呈现出稳定不变的特性。反而当系统极其纯净的时候，电阻的阶梯状是不存在的。

这就是为什么霍尔电阻在强磁场的情况下，不是连续变化，而是跳跃变化的。磁场的大小在一定范围内，霍尔电阻的变化呈阶梯状。

上述的量子霍尔效应是“整数量子霍尔效应”没有考虑电子间的相互作用，当我们考虑时，就是“分数量子霍尔效应”了，我们下一个帖子再说