物理 【论坛资料室】高等数学——函数与极限
$\color{red}{\Huge{都来看!!!!!终于更完辣!!!}}$
$\Huge{更新进度:\color{cyan}{100\%}}$
$\color{red}{[2025.6.24已更新]}$
——————————————————————————————以下是正文——————————————————————————————
$\Huge{入门篇}$
















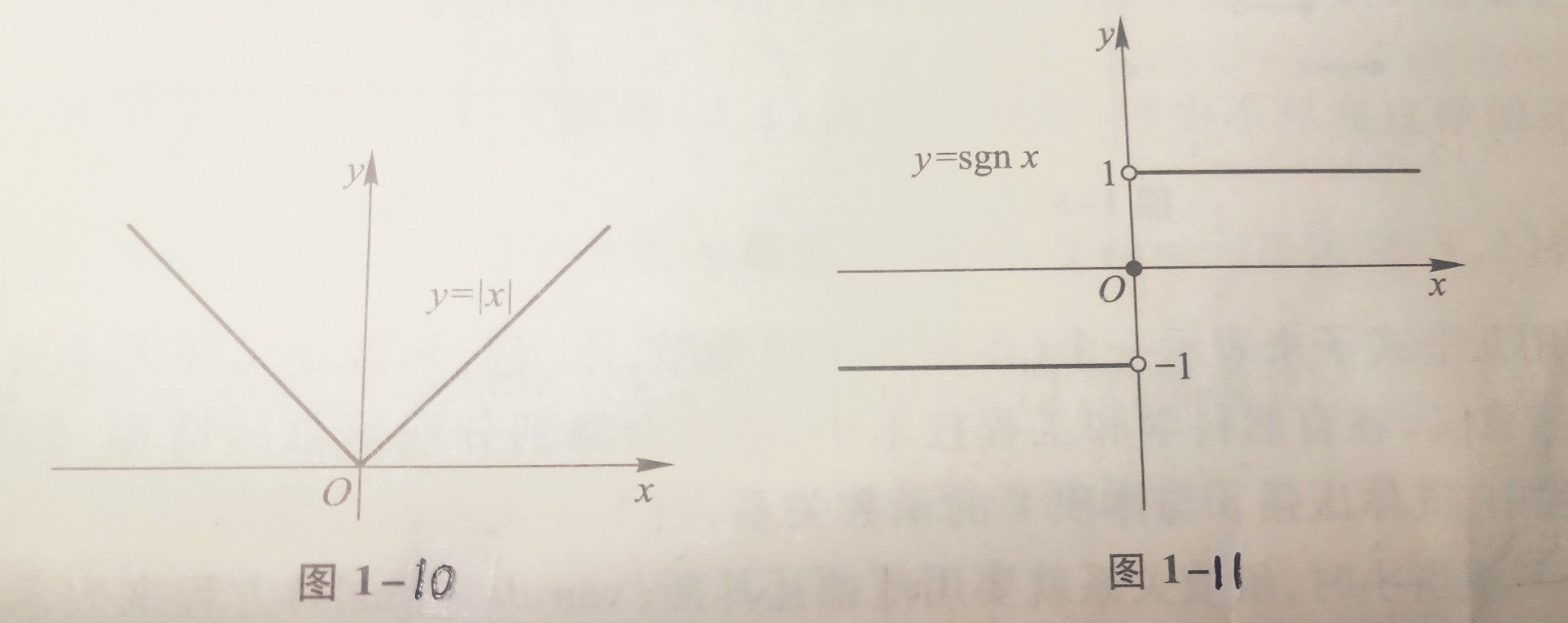

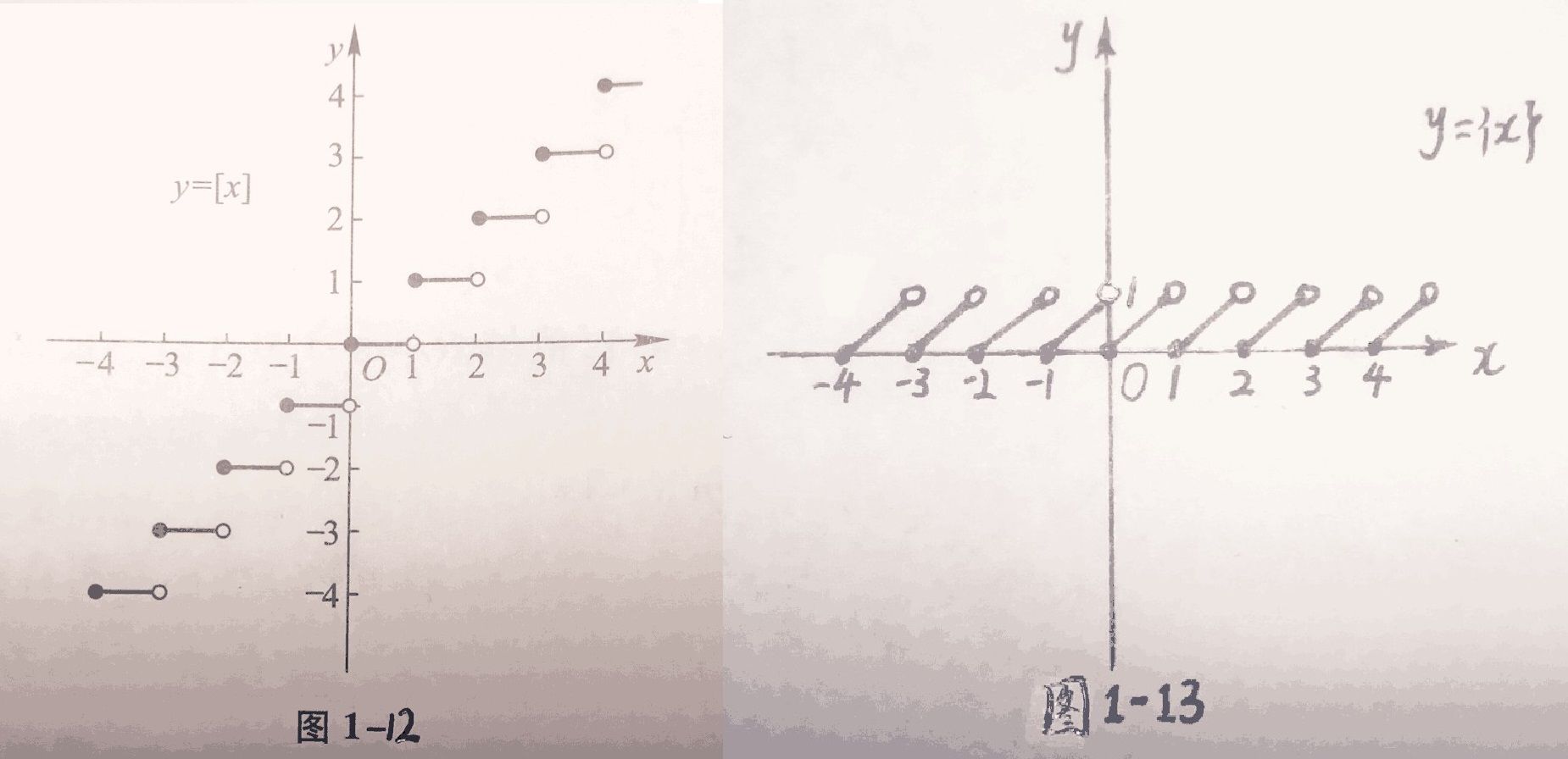

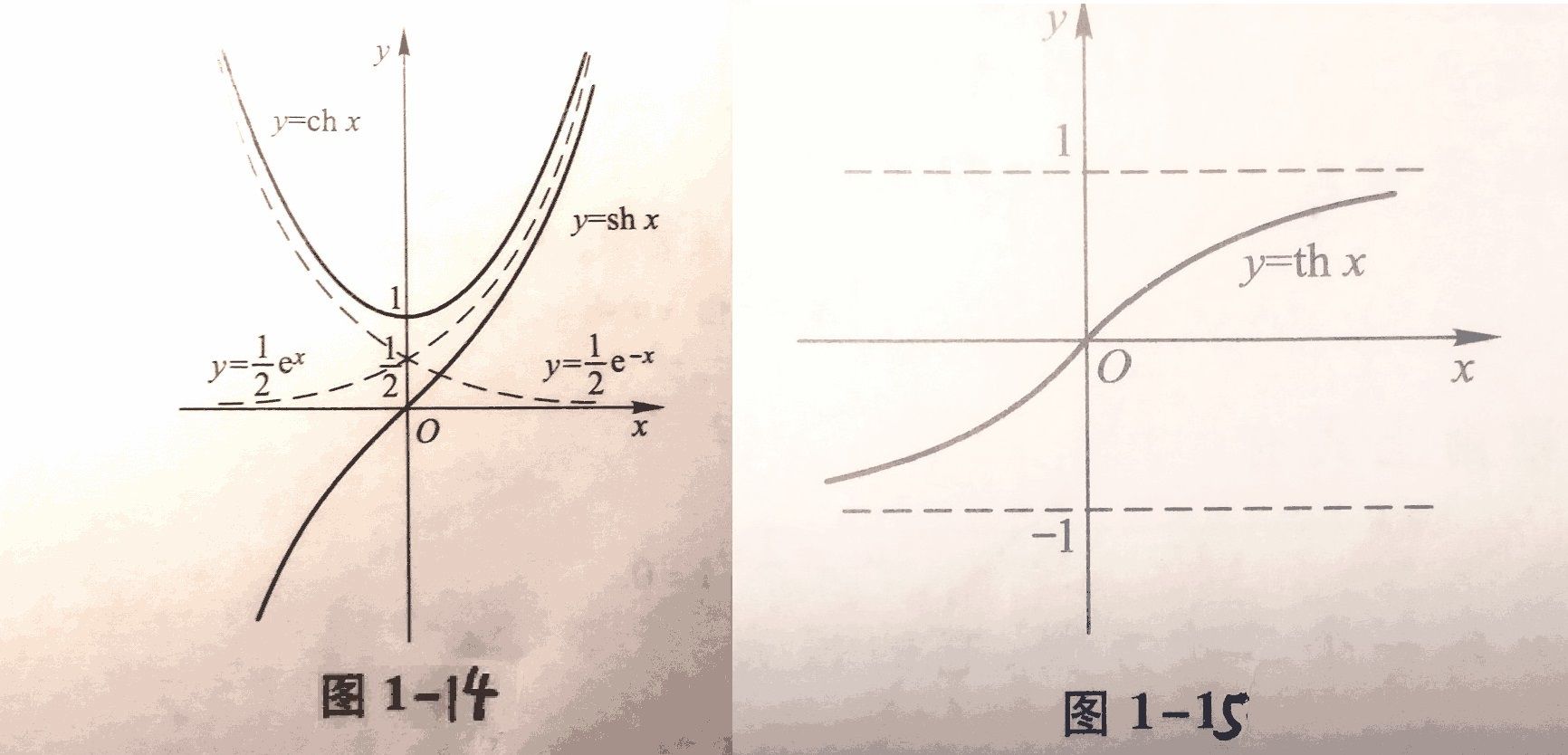
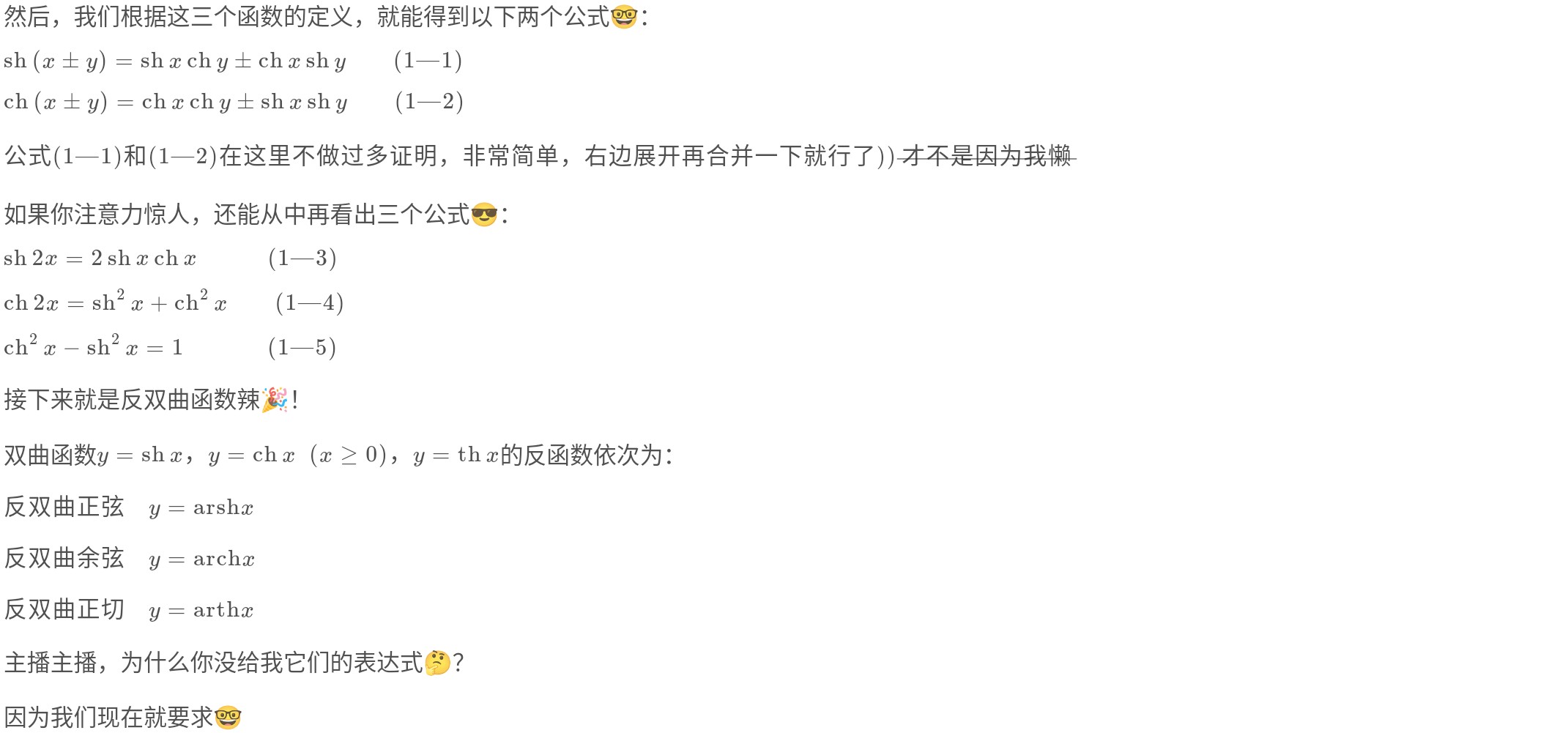

接着,讨论$y=\ch x(x\ge 0)$的反函数🤓.由$x=\ch y(y\ge 0)$,有
$x=\frac{e^y+e^{-y}}{2},y\ge 0$.
$同理可得e^y=x\pm \sqrt{x^2-1}$
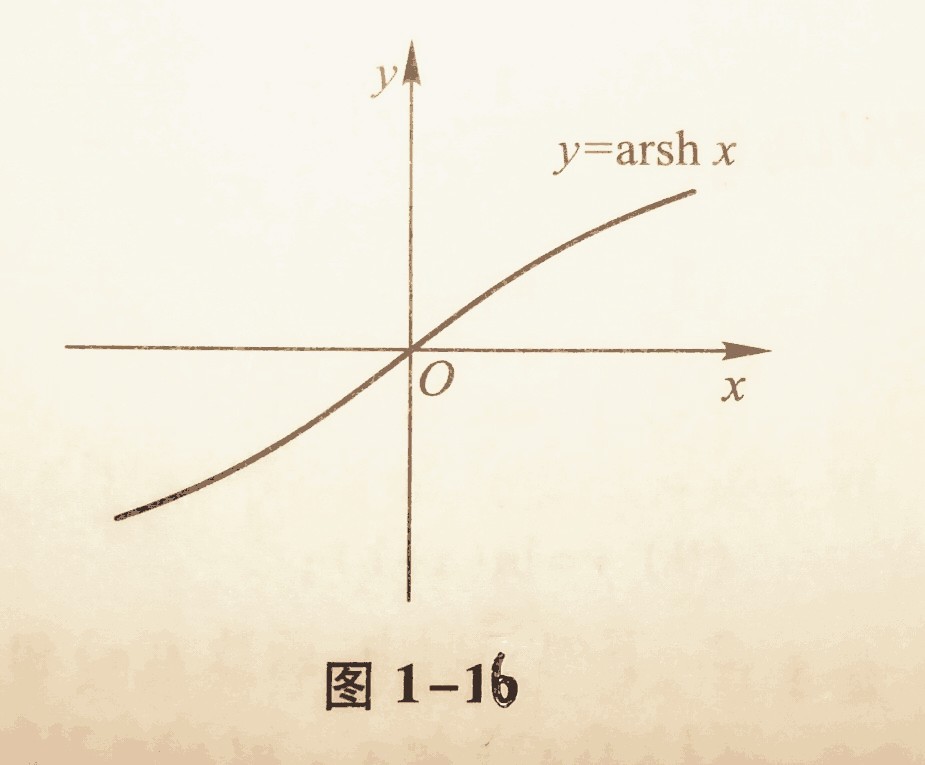
因为$y\ge 0应取正,可得反双曲余弦$
$y=\text{arch}x=\ln (x+\sqrt{x^2-1})$.
函数$y=\text{arsh}x的定义域D=[1,+\infty ),值域R_f=[1,+\infty ),在区间[1,+\infty )单调递增(1—17).$
同样,我们可得反双曲正切
$y=\text{arth}x=\frac{1}{2}\ln\frac{1+x}{1-x}.$
它的定义域$D=(-1,1),值域R_f=(-\infty ,+\infty ),是奇函数,在开区间(-1,1)内单调递增,有垂直渐近线x=-1与x=1(图1—18).$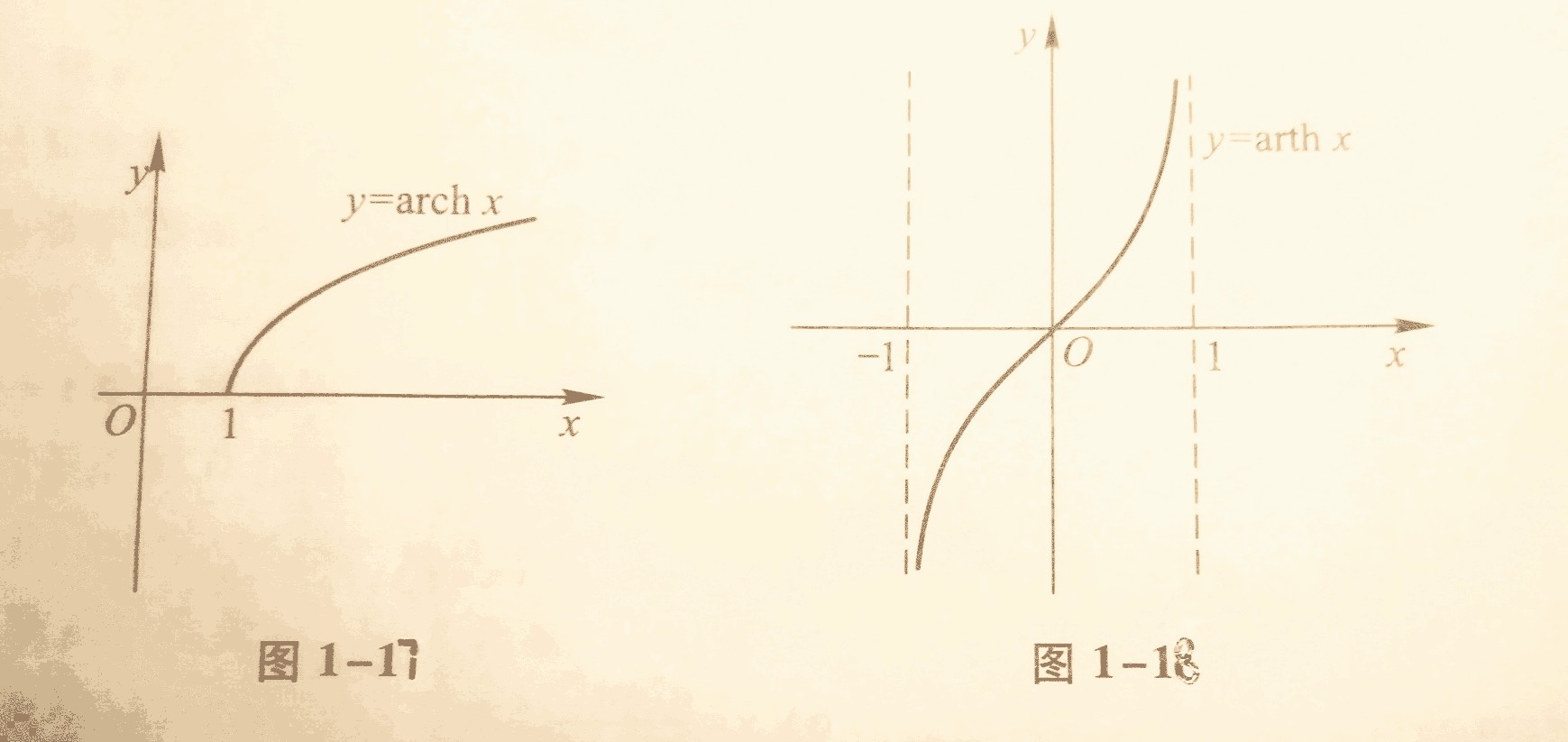
$———————————————\textbf{The~end}———————————————$
$\color{coral}{完结撒花🎊🎊🎈🎉🎉🎉🎉🎉🎉🎉🎈🎊🎊}$
共8条回复
时间正序
