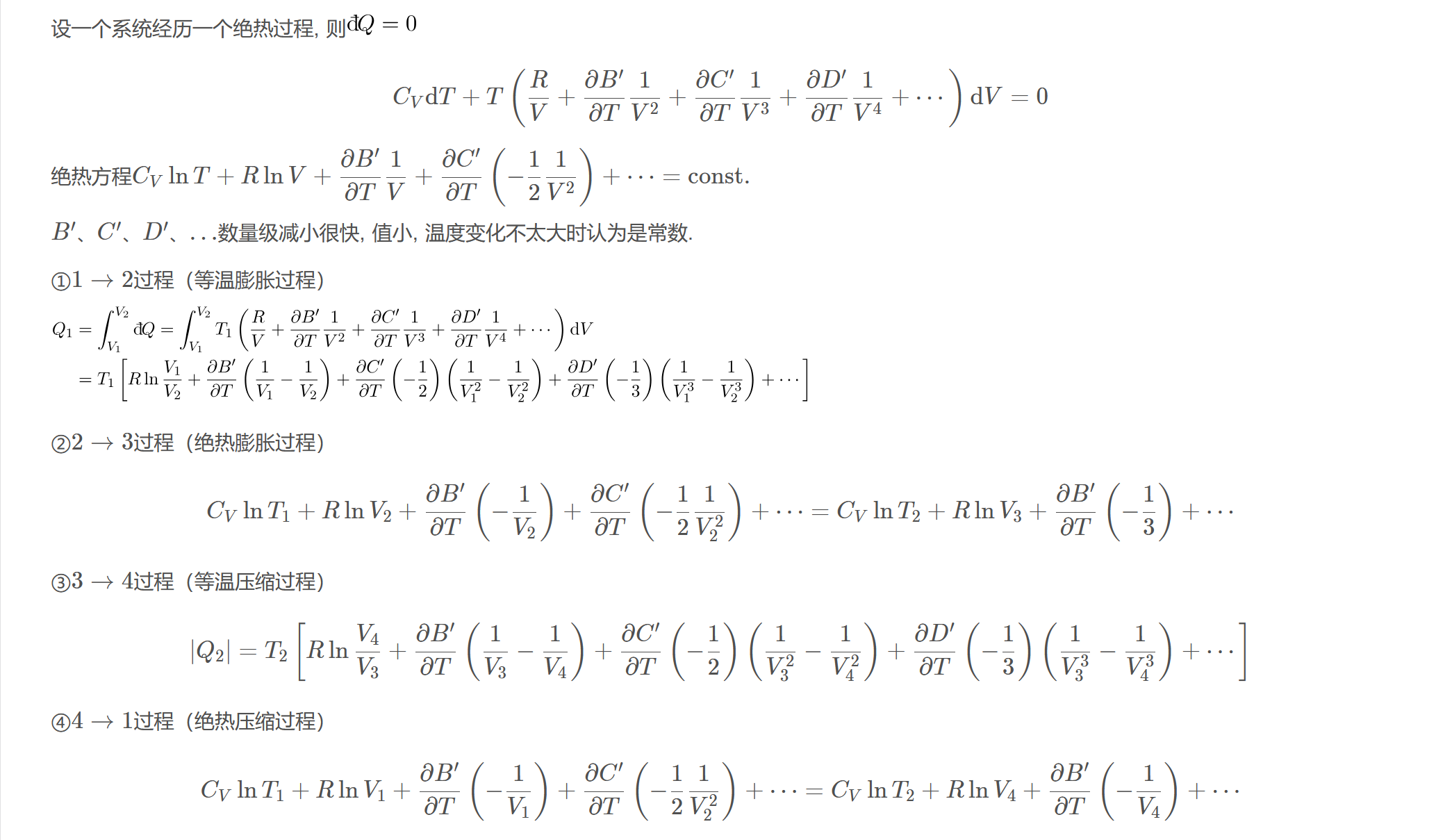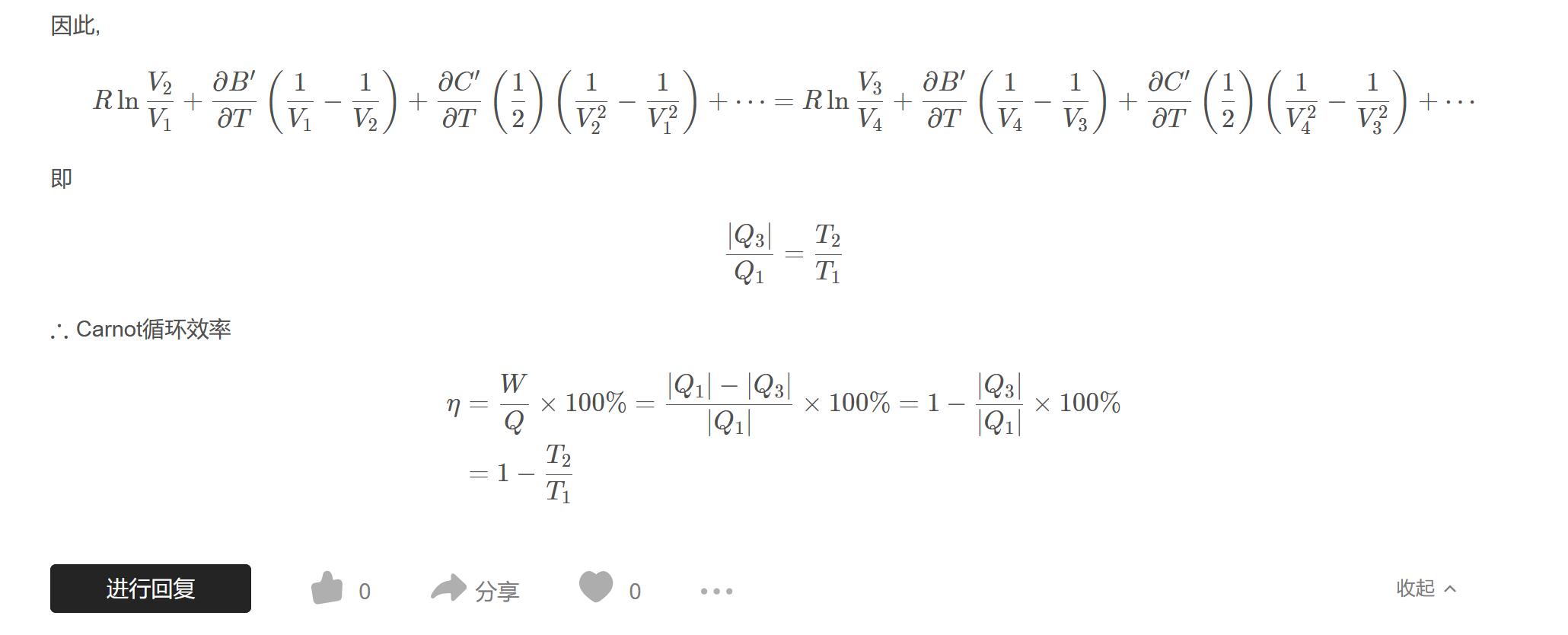物理

Carnot循环效率是否与工作物质无关？（Onnes气体）

考虑更一般性，我们讨论

2. 工作物质为Onnes气体

Onnes气体物态方程为

$$PV=A+\dfrac{B^{\prime}}{V}+\dfrac{C^{\prime}}{V^{2}}+\dfrac{D^{\prime}}{V^{3}}+\cdots$$

其中, $A=RT$、$B^{\prime}$、$C^{\prime}$、$D^{\prime}$、$\ldots$都是$T$的函数.

$$P=\dfrac{A}{V}+\dfrac{B^{\prime}}{V^{2}}+\dfrac{C^{\prime}}{V^{3}}+\dfrac{D^{\prime}}{V^{4}}+\cdots$$

$$\left(\dfrac{\partial P}{\partial T}\right)_{V}=\dfrac{R}{V}+\dfrac{\partial B^{\prime}}{\partial T}\dfrac{1}{V^{2}}+\dfrac{\partial C^{\prime}}{\partial T}\dfrac{1}{V^{3}}+\dfrac{\partial D^{\prime}}{\partial T}\dfrac{1}{V^{4}}+\cdots$$

$$\left(\dfrac{\partial U}{\partial V}\right)_{T}=T\left(\dfrac{\partial P}{\partial T}\right)_{V}-P=T\left(\dfrac{R}{V}+\dfrac{\partial B^{\prime}}{\partial T}\dfrac{1}{V^{2}}+\dfrac{\partial C^{\prime}}{\partial T}\dfrac{1}{V^{3}}+\dfrac{\partial D^{\prime}}{\partial T}\dfrac{1}{V^{4}}+\cdots\right)-P$$

$$dU=\left(\dfrac{\partial U}{\partial V}\right)_{T}\mathrm{d}V+\left(\dfrac{\partial U}{\partial T}\right)_{V}\mathrm{d}T=C_{V}\mathrm{d}T+\left[T\left(\dfrac{R}{V}+\dfrac{\partial B^{\prime}}{\partial T}\dfrac{1}{V^{2}}+\dfrac{\partial C^{\prime}}{\partial T}\dfrac{1}{V^{3}}+\dfrac{\partial D^{\prime}}{\partial T}\dfrac{1}{V^{4}}+\cdots\right)-P\right]\mathrm{d}V$$

设一个系统经历一个绝热过程, 则

$$C_{V}\mathrm{d}T+T\left(\dfrac{R}{V}+\dfrac{\partial B^{\prime}}{\partial T}\dfrac{1}{V^{2}}+\dfrac{\partial C^{\prime}}{\partial T}\dfrac{1}{V^{3}}+\dfrac{\partial D^{\prime}}{\partial T}\dfrac{1}{V^{4}}+\cdots\right)\mathrm{d}V=0$$

绝热方程$C_{V}\ln T+R\ln V+\dfrac{\partial B^{\prime}}{\partial T}\dfrac{1}{V}+\dfrac{\partial C^{\prime}}{\partial T}\left(-\dfrac{1}{2}\dfrac{1}{V^{2}}\right)+\cdots=\text{const}.$

$B^{\prime}$、$C^{\prime}$、$D^{\prime}$、$\ldots$数量级减小很快, 值小, 温度变化不太大时认为是常数.

①$1\to 2$过程（等温膨胀过程）

②$2\to 3$过程（绝热膨胀过程）

$$C_{V}\ln T_{1}+R\ln V_{2}+\dfrac{\partial B^{\prime}}{\partial T}\left(-\dfrac{1}{V_{2}}\right)+\dfrac{\partial C^{\prime}}{\partial T}\left(-\dfrac{1}{2}\dfrac{1}{V_{2}^{2}}\right)+\cdots=C_{V}\ln T_{2}+R\ln V_{3}+\dfrac{\partial B^{\prime}}{\partial T}\left(-\dfrac{1}{3}\right)+\cdots$$

③$3\to 4$过程（等温压缩过程）

$$|Q_{2}|=T_{2}\left[R\ln\dfrac{V_{4}}{V_{3}}+\dfrac{\partial B^{\prime}}{\partial T}\left(\dfrac{1}{V_{3}}-\dfrac{1}{V_{4}}\right)+\dfrac{\partial C^{\prime}}{\partial T}\left(-\dfrac{1}{2}\right)\left(\dfrac{1}{V_{3}^{2}}-\dfrac{1}{V_{4}^{2}}\right)+\dfrac{\partial D^{\prime}}{\partial T}\left(-\dfrac{1}{3}\right)\left(\dfrac{1}{V_{3}^{3}}-\dfrac{1}{V_{4}^{3}}\right)+\cdots\right]$$

④$4\to1$过程（绝热压缩过程）

$$C_{V}\ln T_{1}+R\ln V_{1}+\dfrac{\partial B^{\prime}}{\partial T}\left(-\dfrac{1}{V_{1}}\right)+\dfrac{\partial C^{\prime}}{\partial T}\left(-\dfrac{1}{2}\dfrac{1}{V_{2}^{2}}\right)+\cdots=C_{V}\ln T_{2}+R\ln V_{4}+\dfrac{\partial B^{\prime}}{\partial T}\left(-\dfrac{1}{V_{4}}\right)+\cdots$$

因此,

$$R\ln\dfrac{V_{2}}{V_{1}}+\dfrac{\partial B^{\prime}}{\partial T}\left(\dfrac{1}{V_{1}}-\dfrac{1}{V_{2}}\right)+\dfrac{\partial C^{\prime}}{\partial T}\left(\dfrac{1}{2}\right)\left(\dfrac{1}{V_{2}^{2}}-\dfrac{1}{V_{1}^{2}}\right)+\cdots=R\ln\dfrac{V_{3}}{V_{4}}+\dfrac{\partial B^{\prime}}{\partial T}\left(\dfrac{1}{V_{4}}-\dfrac{1}{V_{3}}\right)+\dfrac{\partial C^{\prime}}{\partial T}\left(\dfrac{1}{2}\right)\left(\dfrac{1}{V_{4}^{2}}-\dfrac{1}{V_{3}^{2}}\right)+\cdots$$

即

$$\dfrac{|Q_{3}|}{Q_{1}}=\dfrac{T_{2}}{T_{1}}$$

$\therefore$ Carnot循环效率

$$\begin{aligned}\eta&=\dfrac{W}{Q}\times100\%=\dfrac{|Q_{1}|-|Q_{3}|}{|Q_{1}|}\times 100\%=1-\dfrac{|Q_{3}|}{|Q_{1}|}\times 100\%\\&=1-\dfrac{T_{2}}{T_{1}}\end{aligned}$$

板砖特供