数学

关于0.9九的循环等于一？？？

1/3=0.3循环

1/3十1/3+1/3=1=0.9循环

这种试图用初等知识解释极限的其实可以不用理会了，完全没有半点道理。

如果严谨证明的话需要用到R的稠密性和δ-ε理论。

其实很简单

因为： 1%3 = 1/3

              1/3  = 0.333333.......... 

              0.333333........*3 = 0.999999999.....

              1/3 * 3 = 1

所以：0.9999999...... = 1

注： “ % "为除号   “    ........    "为省略号。

1/3=0.333…

2/3=0.666…

3/3=0.999…=1

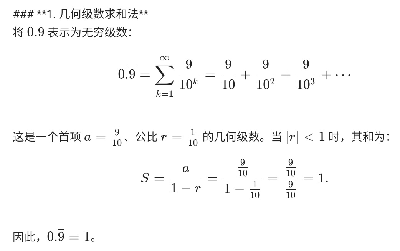
1. 几何级数求和法

将 \(0.\overline{9}\) 表示为无穷级数：\[0.\overline{9} = \sum_{k=1}^{\infty} \frac{9}{10^k} = \frac{9}{10} + \frac{9}{10^2} + \frac{9}{10^3} + \cdots\]这是一个首项 \(a = \frac{9}{10}\)、公比 \(r = \frac{1}{10}\) 的几何级数。当 \(|r| < 1\) 时，其和为：\[S = \frac{a}{1 - r} = \frac{\frac{9}{10}}{1 - \frac{1}{10}} = \frac{\frac{9}{10}}{\frac{9}{10}} = 1.\]因此，\(0.\overline{9} = 1\)。

2. 实数完备性：柯西序列等价性

在实数构造中，实数可定义为柯西序列的等价类。考虑以下两个柯西序列：- 序列 \(a_n = 0.\underbrace{99\ldots9}_{n\text{个}}\)；- 常数序列 \(b_n = 1\)。它们的差为：\[|a_n - b_n| = 1 - 0.\underbrace{99\ldots9}_{n\text{个}} = \frac{1}{10^n}.\]当 \(n \to \infty\) 时，\(\frac{1}{10^n} \to 0\)，因此两个序列等价。由实数定义可知，\(0.\overline{9}\) 与 \(1\) 代表同一实数。

3. 戴德金分割法

戴德金分割将实数定义为有理数集的一个划分 \((A, B)\)，其中 \(A\) 无最大元，\(B\) 为所有上界。假设存在 \(x = 0.\overline{9}\) 和 \(y = 1\)：- 若 \(x \neq y\)，则存在有理数 \(q\) 满足 \(x < q < y\)。- 但任何 \(q < 1\) 必然小于某个 \(0.\underbrace{99\ldots9}_{n\text{个}} < x\)，矛盾。因此，\(x\) 和 \(y\) 的分割相同，故 \(0.\overline{9} = 1\)。

4. ε-δ 极限定义

设 \(x = 0.\overline{9}\)。对任意 \(\epsilon > 0\)，选择 \(N\) 使得 \(\frac{1}{10^N} < \epsilon\)。当 \(n > N\) 时：\[1 - 0.\underbrace{99\ldots9}_{n\text{个}} = \frac{1}{10^n} < \epsilon.\]由极限定义，\(x = \lim_{n \to \infty} 0.\underbrace{99\ldots9}_{n\text{个}} = 1\)。

5. 十进制表示唯一性

在标准实数系中，十进制展开唯一，除非某数可表示为有限小数或无限循环9。例如：\[1.000\ldots = 0.999\ldots\]为避免表示不唯一，数学上约定这两种形式代表同一实数，即 \(0.\overline{9} = 1\)。

这个是AI伴学给我的解释，不知道对不对:(

将就着看看吧，欢迎指正！

对于无穷的运算和有限的运算是不一样的，

是不能以我们的惯性思维，用简单的加减乘除去解释的。

举个不恰当的例子，希尔伯特的旅馆都听过吧，

∞+1=∞，∞+∞=∞，∞×∞=∞，(这里也许表达得不太严谨，因为∞不能参与运算)

这听起来很反直觉，但这是事实。

正是因为我们生活在一个“万物皆(可)数”的世界里，无穷这种东西才显得如此抽象。

世间万物都是有限的，除了思想。

在物理世界中，你永远画不出完美的几何图形，也找不到那绝对光滑的理想平面，宇宙中更没有无穷的东西，

但在我们的思想中，这是可以做到的。

鄙人认为：数学，就是一门用“物理”的大脑，去创造一个“反物理”的理想世界的学科。

如何去创造这个世界，乃是我们学习数学的目的。

所以也别争了，真要证明这东西，还是得用实数的稠密性，没用到极限思想的都纯属无稽之谈。

抱歉写了篇小作文，是不是跑题了？把我当个LZ看就行💦💦💦

你的方法目前可以这么理解，但本质不对

严谨的要用极限

具体看看高数书

1÷3=0.333333333.......

0.9999999........÷3=0.33333333........

所以1=0.99999999.......