- 时间正序
- 时间倒序
- 评论最多
首更---将军饮马![]()
一、背景故事的数学隐喻
“将军饮马”虽以古代战争为背景,实则为古希腊数学家海伦提出的最短路径问题的寓言化表达。其核心思想与光反射定律(入射角=反射角)一致,揭示了自然界中能量最小化的普遍规律。通过将实际问题抽象为几何模型,训练从具象到抽象的数学思维。
二、核心知识点详解
1. 几何反射原理的本质
我们先用物理类比导入新课:光线从一点出发,经镜面反射到另一点的最短路径,对应将军饮马的最优解。
数学操作:构造对称点 \(B'\),将折线路径 \(A \rightarrow P \rightarrow B\) 转化为直线 \(A \rightarrow B'\),利用“两点之间线段最短”公理求解。
公式推导:若直线 \(l\) 的方程为 \(ax + by + c = 0\),点 \(B(x_0, y_0)\) 的对称点 \(B'\) 坐标为: \[ B'\left( x_0 - \frac{2a(ax_0 + by_0 + c)}{a^2 + b^2},\ y_0 - \frac{2b(ax_0 + by_0 + c)}{a^2 + b^2} \right)
2. 轴对称变换的深层意义
几何意义:对称变换不改变距离,但改变了路径的“可见性”,使隐藏的最短路径显性化。
动态验证:若饮马点 \(P\) 偏离理论最优位置,总路径长度必然增加(可通过几何画板动态演示)。
三、解题步骤的精细化拆解
例题:点 \(A(1,3)\) 和 \(B(4,1)\),河岸为 \(x\) 轴,求饮马点 \(P\)。
解析:1. 构造对称点 \(B'\) 因河岸为 \(x\) 轴(\(y=0\)),对称点 \(B'(4,-1)\)。
2. 求直线 \(AB'\) 的方程:斜率 \(k = \frac{-1-3}{4-1} = -\frac{4}{3}\),方程为 \(y - 3 = -\frac{4}{3}(x - 1)\),化简得 \(y = -\frac{4}{3}x + \frac{13}{3}\)。
3. 求交点 \(P\)令 \(y=0\),解得 \(x = \frac{13}{4}\),故 \(P\left(\frac{13}{4}, 0\right)\)。
4. 验证路径最短:计算 \(AP + PB = \sqrt{\left(\frac{13}{4}-1\right)^2 + (0-3)^2} + \sqrt{\left(4-\frac{13}{4}\right)^2 + (1-0)^2} = 5\),而 \(AB' = \sqrt{(4-1)^2 + (-1-3)^2} = 5\),验证等距性。
四、经典变式题型全解析
1. 多次反射型问题
例题:将军需先后经过两条平行河岸 \(l_1\) 和 \(l_2\),求最短路径。
解法: 先对目标点 \(B\) 关于 \(l_2\) 对称得 \(B'\),再对 \(B'\) 关于 \(l_1\) 对称得 \(B''\);连接 \(A\) 与 \(B''\),交 \(l_1\) 于 \(P_1\),交 \(l_2\) 于 \(P_2\),路径 \(A \rightarrow P_1 \rightarrow P_2 \rightarrow B\) 即为最优解。
2. 非直线型约束问题
问题:若河岸为折线或曲线,如何转化?
解法:对于分段直线河岸,在每段应用反射原理;对曲线河岸,需使用微积分求极值,但中学阶段通常限定为直线。
五、易错点与实战技巧(画星星)
对称轴选择错误:若河岸为 \(y = kx + b\),需用直线一般式求对称点,而非简单坐标取反。
忽略可行性验证:构造的对称点可能位于不可行区域(如山体后方),需结合实际问题调整。
计算失误:建议分步计算对称点坐标,避免符号错误。
六、拓展探究题
1. 动态将军饮马:若河岸随时间移动,如何建立动态优化模型?
2. 三维空间扩展:将问题拓展至三维空间,最短路径是否仍由反射原理决定?
3. 博弈论视角:若敌方预判将军路径并设伏,如何调整模型引入风险因子?
- 1
课后练习(请根据能力自行选择题目,不懂可问)
基础题型 题目1(轴对称基础) (难度:1) 已知点 A(2,5) 和点 B(6,1),河岸为 x 轴。将军从 A 出发到河岸饮马后前往 B,求最短路径长度及饮马点坐标。
变式题型
题目2(多次反射) (难度:2)
将军需先到直线 l1:y=2 饮马,再到直线 l2:y=−1 取物资,最后到达 B(3,4)。起点为 A(1,5),求最短路径。
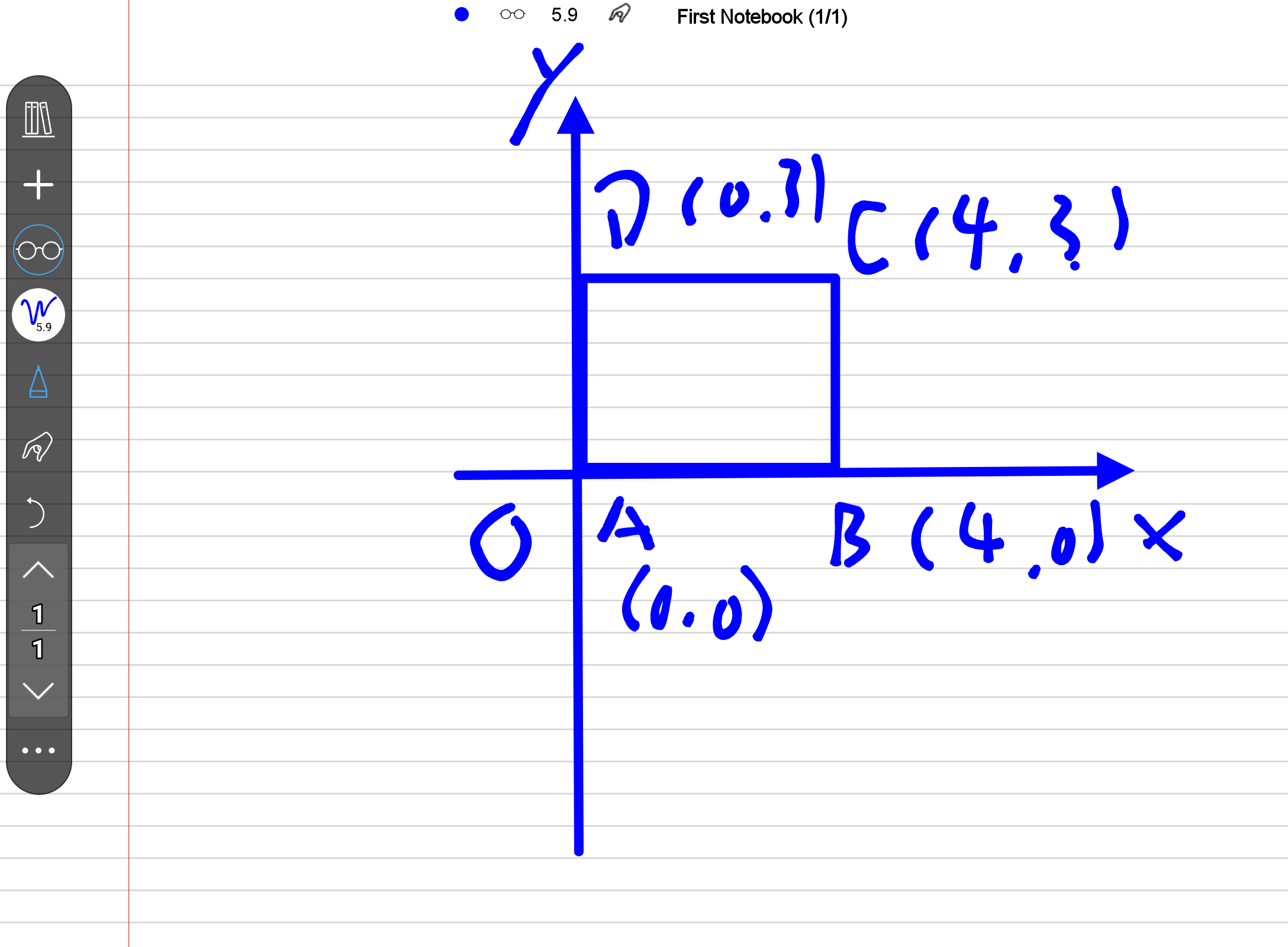
附加一到几何结合的(难度:1.5)
如图,已知矩形ABCD中,AB=12,AD=3,EF 分别为AB,DC上的两个动点。求AF+FE+EC 的最小值。
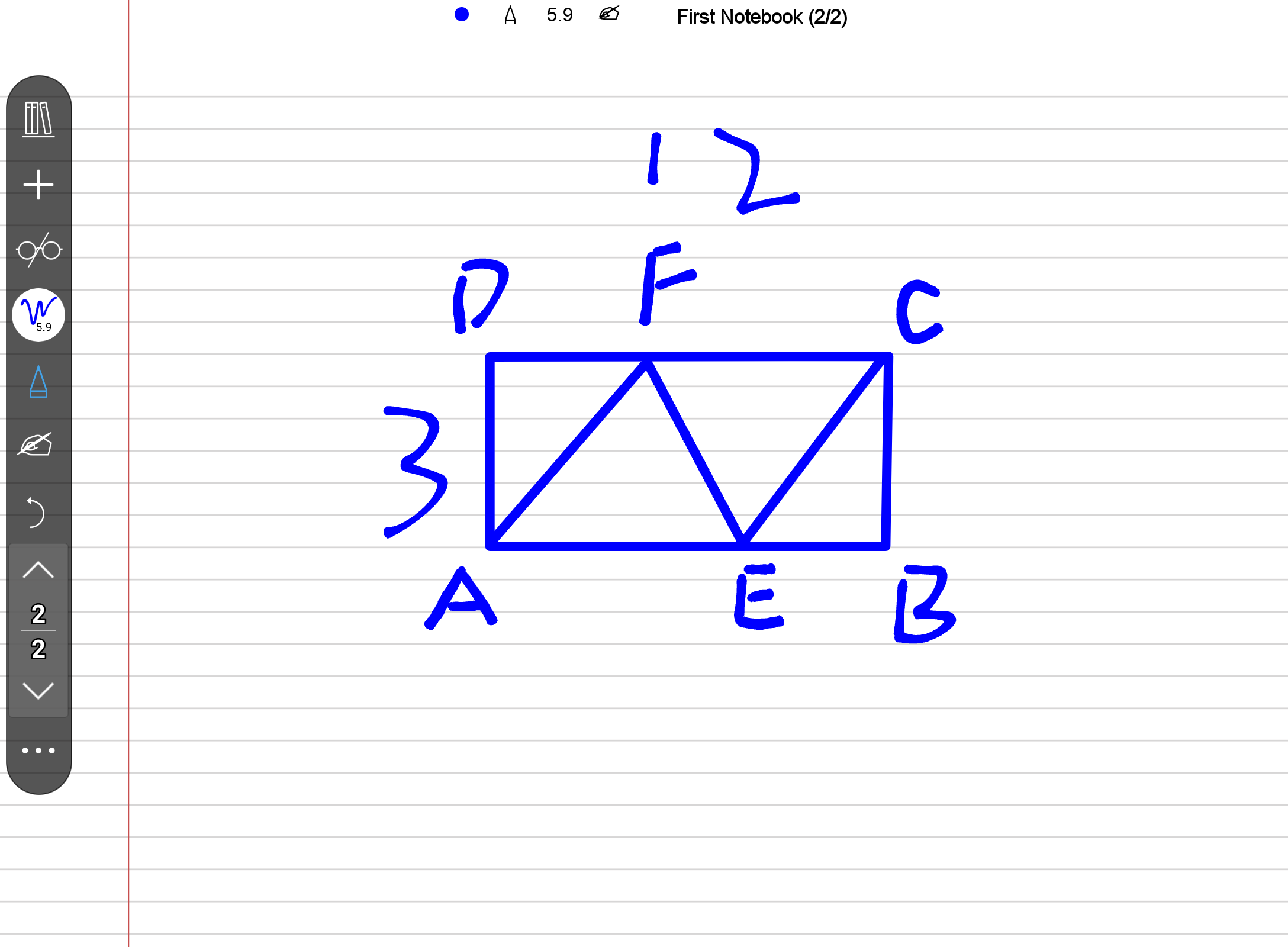
课后练习!!!
练习题1(基础几何应用) 题目: 点 A 在直线 l 外,AB⊥l 于 B,且 AB=6。动点 P 在直线 l 上,从 A 出发,先以速度 2 单位/秒到 P,再以速度 1 单位/秒到 B。求总时间最短时 BP 的长度。练习题1(基础几何应用)
练习题2(坐标系中的计算) 题目: 在平面直角坐标系中,点 A(1,3),直线 l:y=2x,点 B 在 l 上。从 A 出发,先以速度 3 单位/秒到直线 l 上的点 P,再以速度 1 单位/秒到 B(2,4)。求总时间最短时 P 的坐标。练习题3(综合压轴题)
题目:
如图,抛物线 y=x2−4x+3 与直线 l:y=x−1 交于
重发一下
练习题3(综合压轴题) 题目: 如图,抛物线 y=x2−4x+3 与直线 l:y=x−1 交于 A 和 B。点 P 在抛物线上,从 A 出发,以速度 2 单位/秒到 P,再以速度 1 单位/秒到 B。求总时间最短时 P 的坐标。
练习题4(易错点辨析) 题目: 判断正误并修正: “胡不归问题中,若速度 v1=v2,则最短时间路径是直线 AB。因此,将军饮马问题与胡不归问题本质相同。”
一、知识点梳理
瓜豆模型(主从联动模型)描述两个动点(主动点“瓜”和从动点“豆”)之间的几何关系,其核心为:
1. 轨迹一致性:若主动点沿直线/圆运动,从动点轨迹也为直线/圆。
2. 变换关系:从动点由主动点通过旋转、缩放、反射等变换得到。
3. 关键结论:
直线轨迹:主动点与从动点移动路径均为直线,且两直线夹角等于变换角度。
圆轨迹:若主动点绕定点旋转,从动点轨迹为同圆心或缩放后的圆。
二、典型考点
1. 轨迹类型判断(直线或圆)。
2. 路径长度计算(利用相似比或缩放比例)。
3. 最值问题(如线段最小距离、面积最大值)。
4. 综合应用:与旋转相似、圆的性质、函数图像结合。
三、核心解题步骤
1. 确定变换关系:分析从动点如何由主动点变换得到(如旋转60°+缩放0.5倍)。
2. 构造相似/全等三角形:将动态问题转化为静态图形分析。
3. 轨迹模拟:根据主动点轨迹推断从动点轨迹。
4. 几何最值:利用“垂线段最短”“三点共线”等求极值。
四、真题与例题
例题1(基础轨迹判断)
已知点 A 在直线 l 上运动,点 B 由 A 绕点 O 逆时针旋转 90∘ 得到。求 B 的轨迹。
答案:直线 l 绕 O 逆时针旋转 90∘ 后的直线。
例题2(路径长度计算)
主动点 P 在半径为2的圆上运动,点 Q 由 P 绕圆心缩放到 50% 得到。求 Q 的轨迹长度。
答案:2π×0.5=π。
六、易错点与技巧
1. 易错点:
忽略变换顺序(如先旋转再平移 vs 先平移再旋转)。
未正确构造相似三角形导致轨迹判断错误。
2. 技巧:
轨迹模拟法:主动点取特殊位置(如端点、中点),观察从动点位置。
逆向构造:固定从动点,反推主动点位置验证逻辑。
@和光
轨迹方程定义是
1.有一个点在运动。
2. 这个点在运动过程中会留下一条路径(这条路径就是“轨迹”)。轨迹可以是直线、圆、椭圆、抛物线、双曲线,或者更复杂的曲线。
3. 用数学语言(方程)来描述这条路径的形状和位置,这个方程就叫做轨迹方程。
简单来讲就是用来描述动点运动轨迹的数学语言(就是分很多种)


 格式发出来公式全没了,将就着这样看吧
格式发出来公式全没了,将就着这样看吧