数学

【论坛资料室】等幂求和问题

$\color{red}{\Huge{终于更完辣！！！}}$

$\Huge{更新进度:\color{cyan}{100\%}}$

2025.5.23已更新，终于快更完了！(可恶，不能改学科力😭♿♿♿♿♿)

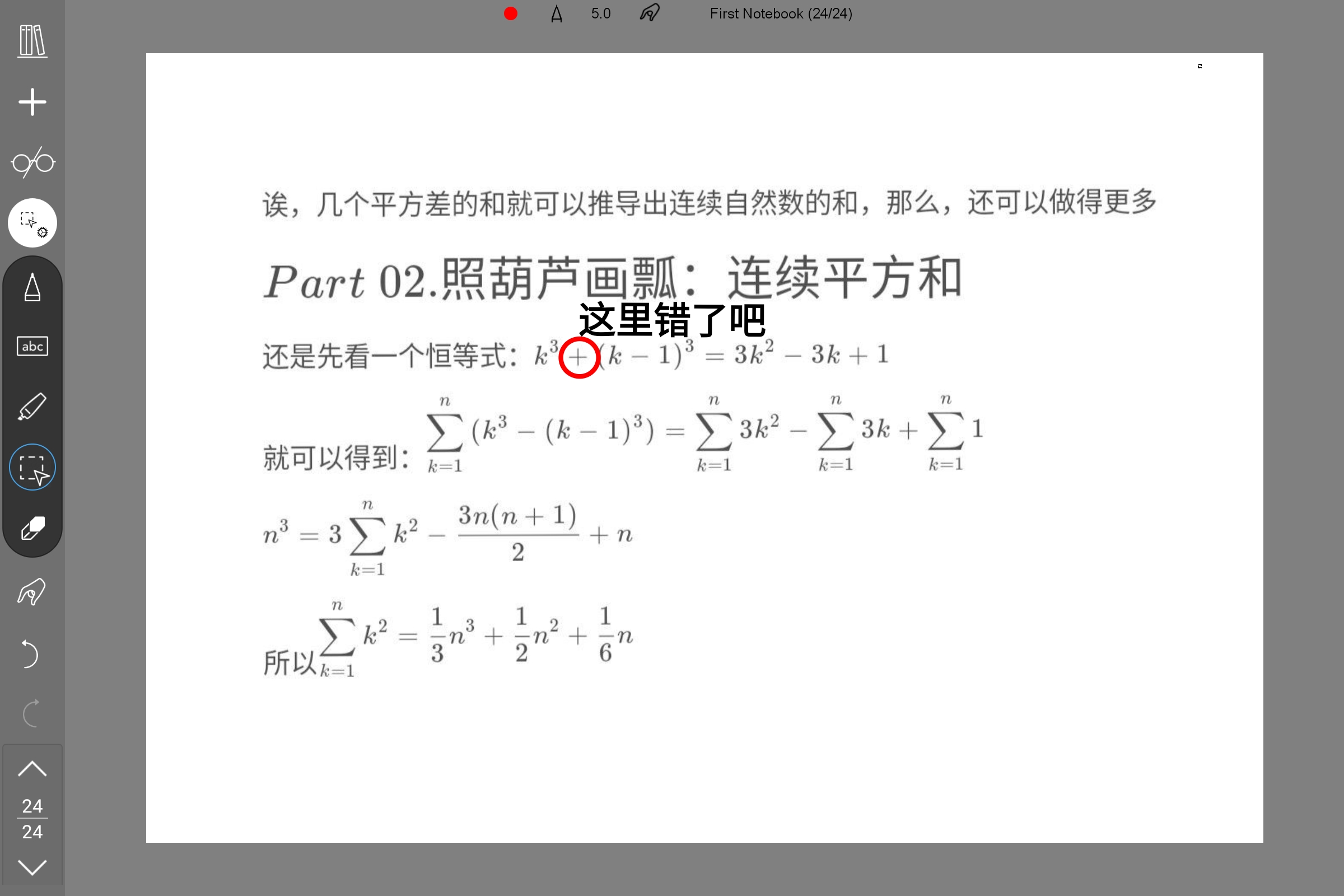
注：INK里备份的$\LaTeX$被吞了呜呜呜，只能放个图了

累了，每次小幅度更新

——————————————————————————————————以下是正文——————————————————————————————————

直接告诉你吧，是$\frac{t}{e^t-1}=\sum^{\infty}_{n=0}B_n\frac{t^n}{n!}(\left| t\right| \lt 2\pi)$

主播主播，为什么还要要求$\left| t\right| \lt 2\pi$啊？🤔

道理很简单，生成函数的分母$e^t-1$在$t=2\pi ik(k\in \mathbb{Z}^{*})$处有零点

这些零点对应的奇点是函数$\frac{t}{e^t-1}$ 的极点

其中，最近的奇点位于$t=\pm 2\pi i$，距离原点的距离为$2\pi$

根据复分析中的结论，幂级数的收敛半径由展开中心(此处为$t=0$)到最近的奇点的距离决定

最近的奇点距离原点的距离为$2\pi$，因此收敛半径为$2\pi$(这里佬们就不用看了♿♿♿)

现在，我们就可以回答前一部分的问题了😃

将$\frac{t}{e^t-1}进行泰勒展开，便会发现B_1=-\frac{1}{2}！$

因为在$Fauhaber$公式中，伟大的$J.Fauhaber$为了解决这个与众不同的$B_1$,令$B_1^+=\frac{1}{2}$

也就是说，$B_j与B_j^+的区别就仅在于B_1=-B_1^+$

接下来我们就可以了解一下$B_n$的几个性质了😋：

$1.B_{2n+1}=0\quad(n\in \mathbb{N}^*)$

证明过程也难度不大🤓

证明：考虑$B_n$的生成函数$\frac{t}{e^t-1}$，若将其与$\frac{t}{2}$相加，得到：

$\frac{t}{e^t-1}+\frac{t}{2}=\frac{t(e^t+1)}{2(e^t-1)}=\frac{t}{2}\cdot\frac{e^{\frac{t}{2}}+e^{-\frac{t}{2}}}{e^{\frac{t}{2}}+e^{-\frac{t}{2}}}=\frac{t}{2}\coth\frac{t}{2}$

$\iff\frac{t}{e^t}=\frac{t}{2}\coth\frac{t}{2}-\frac{t}{2}$

其中$\frac{t}{2}\coth\frac{t}{2}$为偶函数，仅含偶数次幂

$-\frac{t}{2}$为奇函数

因此原生成函数的展开式中，除1次项外，其他奇数次幂的系数必然为零

即$B_{2n+1}=0\quad(n\in \mathbb{N}^*)$

$Q.E.D$

这个小小的结论可以在我们使用$Faulhaber$公式时方便计算

主播主播，我是新手轮蒟蒻，上面关于伯努利数的还是太次操作了，看不懂怎么办？

那你就看看下面这个$\Downarrow$

$2.\forall n\gt 0,有\sum^n_{j=0}\binom{n+1}{j}B_j=0$

这个结论不是$Jacob~Bernoulli$证明的

但是,$\color{red}{Leonhard~Euler显灵！🤓}$他的学生欧拉后来证明了这个性质

证明：$B_n的生成函数为G(t)=\frac{t}{e^t-1}$

则$t=G(t)(e^t-1)=(\sum^{\infty}_{m=1}\frac{t^m}{m!})(\sum^{\infty}_{n=0}B_n\frac{t^n}{n!})=\sum^{\infty}_{k=1}(\sum^{k-1}_{j=0}\frac{B_j}{j!(k-j)!})t^k$

$\therefore 当k\gt 1时,\sum^{k-1}_{j=0}\frac{B_j}{j!(k-j)!}=0$

令$k-1=n$,则$n\gt 0$

等式两边同乘$(n+1)!$

则$\sum^n_{j=0}\binom{n+1}{j}B_j=0$

$Q.E.D.$

完结撒花🎊🎉🎉🎉🎉🎉🎊