物理

一只物竞蝶的交友and问题帖

欢迎所有想交朋友的人啊

这是一个交友帖，但是会附一些物竞的问题

—————————————————————介绍and交友区—————————————————————

本人系物竞生，兼修一点化竞，10后，徐州人，喜欢上海，坐标无锡（上学）锡龄两年，什么都会一点，语文比较差，严重偏科物理化学，目前生病宅在家潜心学习物竞（其实不是很潜心，一天会抽一个小时打phigros）想交知心好友，自认为对外比较开朗善良，会emo但不表现出来

私以为自己理解力很强，给别人讲题也比较好理解，面对面一般都能讲懂，闲暇时喜欢抱着一本大学化学书读，或者自己拿一些奇奇怪怪的结论推来推去，偶尔也会积出来一些奇奇怪怪的东西就是了。。

爱好很多，比如音乐！！本人网易云四年半村龄，听歌时长500h+，收藏750+首英文歌。还有各种棋类（五子，围，中象，国象等等），牌类（扑克，贯蛋，三国杀等等）还有很多博弈类都比较喜欢。球类比较喜欢乒乓

成分应该不算很复杂（

φ人（臀批），方块人，小骑士

b站大会员，宇航兔，鸟蛋，雀粉，-_-，九鸟，耗汁，慕洛六人组，皮医生，qiqisb，药，草蜢，豹豹

总之我很想交朋友，欢迎大家评论，我一般都会回复哒

———————————问问题如果置顶可能会把人赶跑———————————

前一段时间翻程书，突然看到开普勒三定律，就想起来自己好像没推过关于椭圆的东西，然后接下来自己对着公式怎么都想不出来怎么推导，然后回去又把数学里的椭圆恶补了一下但还是没有思路，有没有大佬提供一下推导过程或者思路

开普勒第一定律：天体运动的轨迹是椭圆         没什么思路

开普勒第二定律：天体与中心天体的连线在相同时间内扫过面积相等          🤓☝️诶这个我会，角动量守恒可以做

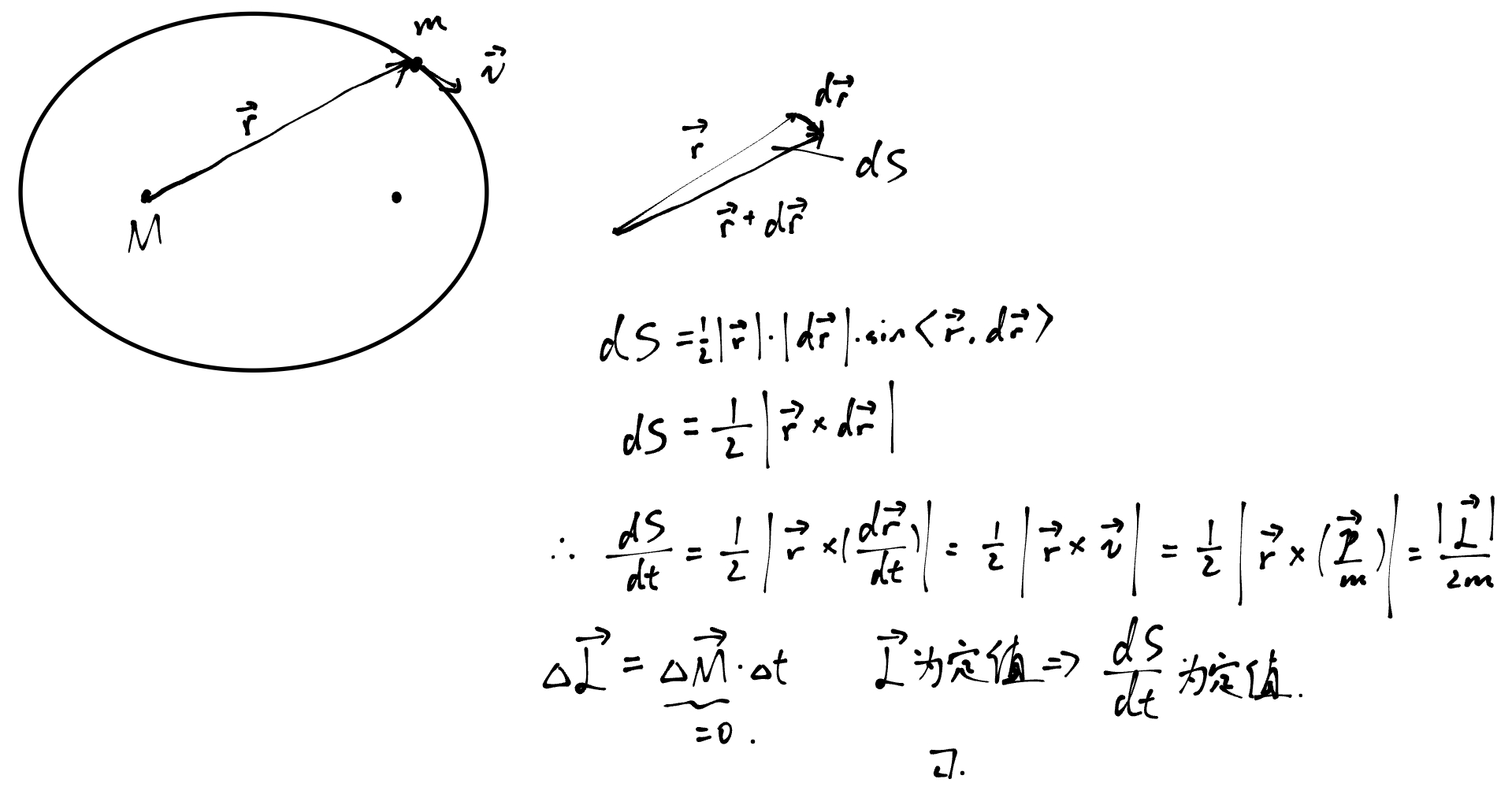
开普勒第三定律：（直接写公式吧 $\frac{a^3}{T^2}=\frac{GM}{4π^2}$      感谢各位大佬，我又去找了一遍一轮竞赛，找到了蔡老师讲的，听了一遍自己终于推出来了

虽然可能有一些多余的过程，但是我终于搞懂了，谢谢大佬们

还剩开一，很多大佬已经提供了思路，我去尝试攻略一下（握拳）

诚心求大佬的帮助，谢谢大佬们！！！