物理 论加密与破译
加密与解密是一对逆运算，加密有很多方法，但破译很难。本贴希望与他人交流。
加密
- 倒置：如123→321或237=、：4%6^$3→3$^6%4：、=732
- 做加法：如凯撒密码或12345→23456
- 语言转换：如1234→abcd(26个字母与26个数字对应) 你好啊→nihaoa
- 矩阵运算：这要求把数据变为矩阵后运算，且由于矩阵不满足乘法交换率而最难破译
- 映射：这要求双方都知道规则，如果做的好几乎无法破译
解密
很简单，只需把加密的操作反着做就好了。
破译
很难，我们连加密了几次都不知道，但也有些方法。
- 频率分析：在字母中，e出现最多，a次之。可以观察加密信息，如果有些字母或数字出现多次，可能就是把英文加密成了字母或数字。
- 尝试：纯运气，但有时加密信息有明显特征(如摩斯密码)，可以试着破译
238120 9141916918519 251521(来自质心,不会破译，但频率分析似乎出了结果，因为1和9反复出现，可能有1→e,9→a，或类似结果)
@质心小姐姐 加密方法是？破译过程是？
- 1
额，那证书加密呢？加密与解密只能在同一台计算机进行，它用的也是这个原理吗？
（本人纯无知，仅此疑问，没有恶意额，纯路人）
只需要加密过程可逆且已知，换一台电脑💻也是可以解密的哦
wk 贴主怎么把帖子放o box里了
加密有多种形式，比如字母顺序和数字对应，数字或字母之间顺序调换，(假设原代码是230578，我从中间分开再合起来变成253708，这个是二分法，还有三分，四分法，但适用于较短句)(或者原代码有张对应的表)两种语言的互译其实也是加密和破译，还有我们常用的摩斯密码，这个可以是笔记，声音，甚至手指敲打，眨眼……还有就是复杂的数字计算式的，比如用函数，方程，倒数，积分等解密。以上方法只要掌握规律就可以破译，还有一种常见的是双方约定的代码和密码本，比如甲把信息转为某本书的多少页，几行几列，可用数字表示，但如果第三方不知道密码本和代码，就无法破译。
同志高几，哪的人啊，交个朋友吧，希望多多交流
栅栏：把密码分成若干份，每行最多k个（自己定），不一定要整除，然后竖着排列
例：i like maths（k＝3）
i l i
k e m
a t h
s
i kasl etimh
键盘：把a－z按26键的顺序排列（a对应q，b对应w）
我怎么记得是97呢
是 97
我记错了
表示之前信息竞赛有背过
啊，我咋记得是ASCLL码表啊
非对称加密法：
加密：
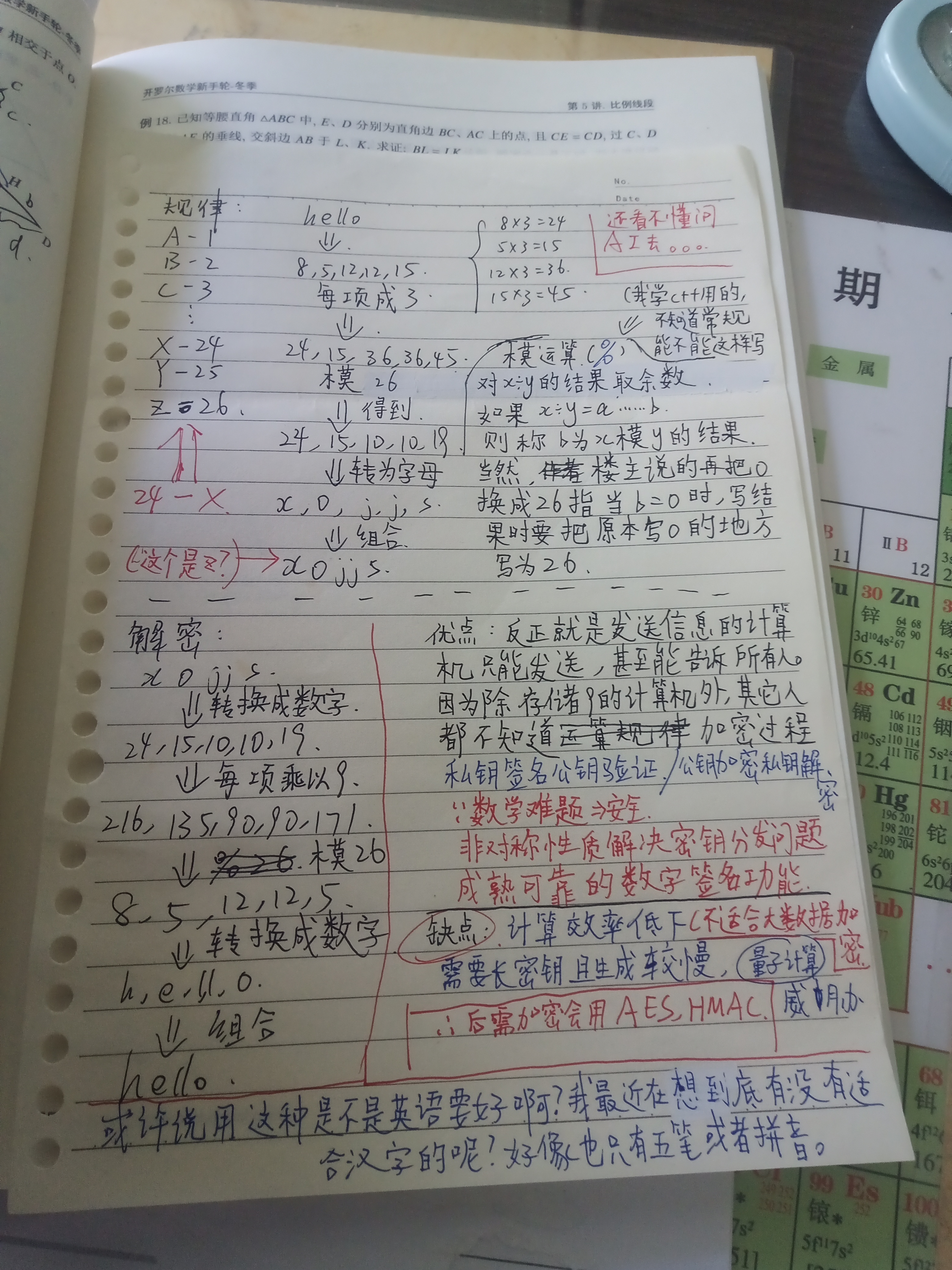
比如把 $\texttt{hello}$ 加密，先把字母转为数字：$8,5,12,12,15$。
把每一项乘以 $3$，得到 $24,15,36,36,45$。
模 $26$，再把 $0$ 换成 $26$，得到 $24,15,10,10,19$。
转为字母：$\texttt{zojjs}$，得到密文。
解密：把 $24,15,10,10,19$ 每一项乘以 $9$，得到 $216,135,90,90,171$。
模 $26$，再把 $0$ 换成 $26$，得到 $8,5,12,12,5$。
转为字母：$\texttt{hello}$。
优点：$3$（公钥）和 $9$（私钥）是两个密钥，可以分别存储在两个计算机，存储 $3$ 的计算机只能发送信息。$3$ 甚至可以公开。
例如用户向银行发送一个加密后的信息，公钥可以存储在每一个用户的手机里，但私钥只存储在服务器里。即使有人找到公钥和密文，也难以推断原文。（在公钥和私钥较大时，如 $10^{1000}$ 左右）
这就是 RSA 的简单版本。
卧，，，槽了终于写完了
汉字用 Unicode 码
或者用电报、盲文等也可以
（突然发现我刚才讲的不是 RSA）
关于量子计算有 Shor 算法能快速分解质因数
一般 RSA 用来加密其他对称加密系统密钥，计算量不会非常大
其实你知道快速幂算法后，会发现其实计算 $a^b\bmod m$ 非常简单
注意，有些解密不是把加密反着来！
注意，有些解密不是把加密反着来！
注意，有些解密不是把加密反着来！
免责声明，以下内容由AI生成
在密码学中，确实存在很多解密过程**并非**简单地将加密过程“倒放”或“逆向执行”的情况。
这通常发生在非对称加密、基于数学难题的方案、或涉及密钥派生和单向函数的场景中。
以下是一些主要的例子：
1. 非对称加密（公钥密码学）：
原理：使用一对数学上相关但不同的密钥：公钥（公开）和私钥（保密）。
加密：用公钥加密明文。
解密：用私钥解密密文。
为什么不是“反过来”：解密过程不是用公钥对密文进行某种逆操作。它使用的是完全不同的密钥（私钥）进行一个不同的数学运算。公钥加密的信息只能用对应的私钥解开，反之亦然（私钥签名只能用公钥验证）。加密和解密是两个不对称的路径。
例子：RSA, ElGamal, ECC (椭圆曲线加密)。
2. 单向散列函数（哈希函数）：
原理：将任意长度的输入（消息）映射为固定长度的输出（哈希值、摘要）。设计上要求是单向的和抗碰撞的。
“加密” (计算摘要)：输入消息 -> 应用哈希函数 -> 输出哈希值。
“解密” (不存在)：没有可行的方法从哈希值反推出原始消息。理论上存在无限多的消息可以产生同一个哈希值（碰撞），但找到它们或找到原像在计算上极其困难。
为什么不是“反过来”：哈希函数没有设计解密过程。它的目的不是保密，而是验证完整性和唯一性。试图“解密”哈希值只能通过暴力猜测（穷举）或利用弱点（碰撞攻击），但这都不是对哈希函数本身的“逆向操作”。
例子：SHA-256, SHA-3, MD5 (已不安全), BLAKE2。
3. 密钥派生函数：
原理：从一个主密钥（如密码、口令）或其他熵源，派生出一个或多个密码学上强的密钥。
“加密” (派生)：输入主密钥 + 盐 + 其他参数 -> 应用 KDF (如 PBKDF2, scrypt, Argon2) -> 输出派生密钥。
“解密” (不存在)：没有可行的方法从派生出的密钥反推出原始的主密钥（如用户密码）。KDF 被设计成单向的。即使你知道派生密钥和盐，也无法有效计算出原始密码。
为什么不是“反过来”：KDF 的核心通常包含哈希函数或类似的计算密集型、内存密集型操作，这些操作本质上是单向的。派生的目的是产生密钥，而不是为了后续能从密钥恢复输入。
例子：PBKDF2, bcrypt, scrypt, Argon2.
4. 数字签名：
原理：用私钥对消息的摘要进行加密（或特定运算）生成签名，验证者用公钥验证签名是否有效。
签名生成 (“加密” 私钥操作)：输入消息 -> 计算哈希 -> 用**私钥**对哈希值进行签名运算 -> 输出签名。
签名验证 (“解密” 公钥操作)：输入消息 + 签名 + 公钥 -> 计算消息哈希 -> 用**公钥**对签名进行验证运算 -> 比较运算结果是否与消息哈希匹配。
为什么不是“反过来”：生成签名用的是私钥，验证签名用的是公钥，密钥不同。验证过程不是简单地将签名运算反过来生成哈希值。它是用公钥对签名进行一个特定的数学运算（在RSA中可能是“解密”签名，在ECC中是点运算验证），然后将结果与独立计算的消息哈希值进行比较。验证过程本身并不“恢复”出原始哈希值，而是检查一个等式是否成立。
例子：RSA签名, ECDSA, EdDSA.
5. 基于身份的加密：
原理：用户的公钥直接是其身份信息（如邮箱地址），由可信的密钥生成中心根据主私钥为该身份生成对应的私钥。
加密：用接收者的身份（作为公钥）和系统参数加密消息。
解密：接收者使用由密钥生成中心为其身份生成的个人私钥解密密文。
为什么不是“反过来”：解密使用的个人私钥是通过一个复杂的、基于主私钥的派生过程生成的，而不是对加密过程的简单反转。加密过程依赖身份和系统参数，解密则依赖个人私钥。
总结一下关键点：
密钥不对称：加解密使用不同的密钥（公钥/私钥），这是最主要的非对称特性。
数学路径不同：解密过程通常是一个独立的数学运算，而不是加密运算的逆过程。它们可能基于不同的数学难题（如大数分解 vs. 离散对数）。
单向性：哈希和KDF的核心是单向函数，它们的设计目标就是不可逆。没有解密过程。
验证而非恢复：数字签名验证是检查等式/关系是否成立，而不是恢复出原始签名输入。
因此，虽然对称加密（如AES）的解密确实是加密的严格逆过程，但现代密码学中大量重要的机制都打破了这种对称性，依靠非对称性、单向函数和复杂的数学关系来实现更强大的安全目标（如密钥分发、身份认证、数据完整性验证）。