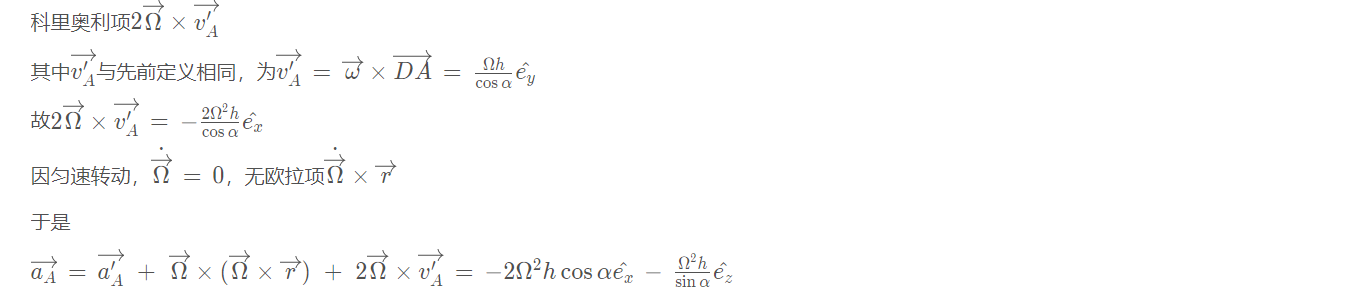物理

自己做的程力习题2-36

正式写之前先说几句废话个人感慨，想看内容可直接跳到分割线后

目前初二，平板上的论坛大约半年前应我妈的要求给删了，当时体验了几天，甚至还想自己去资料室编教材的（虽然水平低下），过了半年了，竞赛学到机械波了，这几天回去速通程力，没想到在习题2-36卡了几天（问题是答案也错了），最后终于弄出来了，想找个地方发一下，电脑上开了个新号开质心论坛看了一圈也没人发，就想着发一下

另说一嘴，现在看到资料室发展得这么全面，真挺欣慰的，竟然有复变函数的教程……唉，真的感谢5汉

其实最初为了赶刷题进度到处问，想问个正确的过程，但是同学都放弃了这个解法，都说把两个转动合成，搞一个瞬时转动轴再去做。我大概也理解这个思路，但总觉得最初的解法不弄明白心里有道坎过不去，就自己尝试了一下

先放题

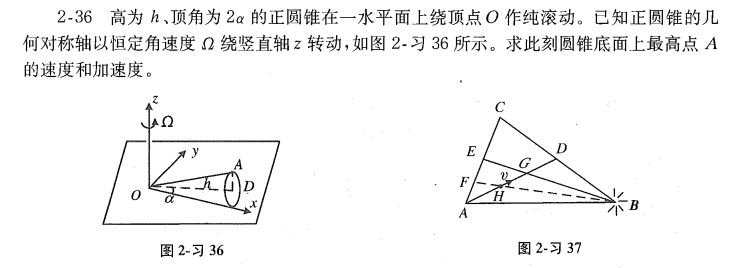
分析

看到这道题，学完运动学的同学可能会有两个想法：

1.由于存在多个转动系，所以可以看作是相对运动，通过转换参考系，补充牵连项，最后导出地面系的速度和加速度

2.由于是刚体，并且是两个纯转动，也只求瞬时速度、加速度，所以可以将两个转动合成出瞬时轴，认为那一瞬间圆锥绕瞬时轴转动，再写出位矢，求导得出速度与加速度

两种都可以，这里不评价哪个更简便。解法1题解给的错了，下面放我的想法。解法2题解给的答案没问题。

解答

对于圆锥上任意一点E的速度，应为其绕z轴转动的速度，加上其绕圆锥中心轴的速度，即

$v_E\,=\,\overrightarrow{\Omega}\times\overrightarrow{OE}\ +\ \overrightarrow{\omega}\times\overrightarrow{DE}$

上式中$\omega$为圆锥自转角速度

记$AD$延长后交$x$轴于$C$，在上式中取$E$为$C$，由纯滚条件，$v_C=0$，可得

$v_C\,=\,(\Omega\frac{h}{\cos\alpha}-\omega h\tan\alpha)\^{e_y}\,=\,0$

即得$\omega=\frac{\Omega}{\sin \alpha}$

此时取$E$为$A$，得

$\overrightarrow{v_A}\,=\,\overrightarrow{\Omega}\times\overrightarrow{OA}\ +\ \overrightarrow{\omega}\times\overrightarrow{DA}\,=\,(\Omega\frac{h}{\cos\alpha}\cos 2\alpha\ +\ \frac{\Omega}{\sin\alpha}h\tan\alpha)\^{e_y}=\,2\Omega\cos\alpha\^{e_y}$

现求加速度。地系中$A$的加速度可视为由$A$系还原至圆锥系，再还原至地系。记圆锥系中，$A$的加速度为$\overrightarrow{a_A'}$；在以$\Omega$的角速度绕$z$轴匀速转动的转动系中观测到的$A$的速度（即A相对圆锥中心轴的速度）为$\overrightarrow{v_A'}$

由$A$系还原至圆锥系：

惯性加速度$\overrightarrow{a_A'}$仅有惯性离心力（无平动，无相对圆锥速度，无角加速度），为

$\omega^2\overrightarrow{AD}\,=\,\frac{\Omega^2}{\sin^2\alpha}h\tan\alpha(\sin\alpha\,\^{e_x}\,-\,\cos\alpha\,\^{e_z})\,=\,\frac{\Omega^2h}{\cos\alpha}\^{e_x}\,-\,\frac{\Omega^2h}{\sin\alpha}\^{e_z}$

圆锥系还原至地系：

惯性离心项$\overrightarrow{\Omega}\times(\overrightarrow{\Omega}\times\overrightarrow{r})$

$\overrightarrow{\Omega}\times(\overrightarrow{\Omega}\times\overrightarrow{OA})\,=\,\overrightarrow{\Omega}\times(\frac{\Omega h\cos 2\alpha}{\cos\alpha})\,=\,\frac{\Omega^2 h\cos 2\alpha}{\cos\alpha}$

科里奥利项$2\overrightarrow{\Omega}\times\overrightarrow{v_A'}$

其中$\overrightarrow{v_A'}$与先前定义相同，为$\overrightarrow{v_A'}\,=\,\overrightarrow{\omega}\times\overrightarrow{DA}\,=\,\frac{\Omega h}{\cos\alpha}\^{e_y}$

故$2\overrightarrow{\Omega}\times\overrightarrow{v_A'}\,=\,-\frac{2\Omega^2h}{\cos\alpha}\^{e_x}$

因匀速转动，$\dot{\overrightarrow{\Omega}}\,=\,0$，无欧拉项$\dot{\overrightarrow{\Omega}}\times\overrightarrow{r}$

于是

$\overrightarrow{a_A}\,=\,\overrightarrow{a_A'}\ +\ \overrightarrow{\Omega}\times(\overrightarrow{\Omega}\times\overrightarrow{r})\ +\ 2\overrightarrow{\Omega}\times\overrightarrow{v_A'}\,=\,-2\Omega^2h\cos\alpha\^{e_x}\,-\,\frac{\Omega^2h}{\sin\alpha}\^{e_z}$

感兴趣的，可以自行按照同样的方法自行计算圆锥上任意一点的速度和加速度，当做一道计算练习题

可能平板上显示有乱码，下面放图片形式