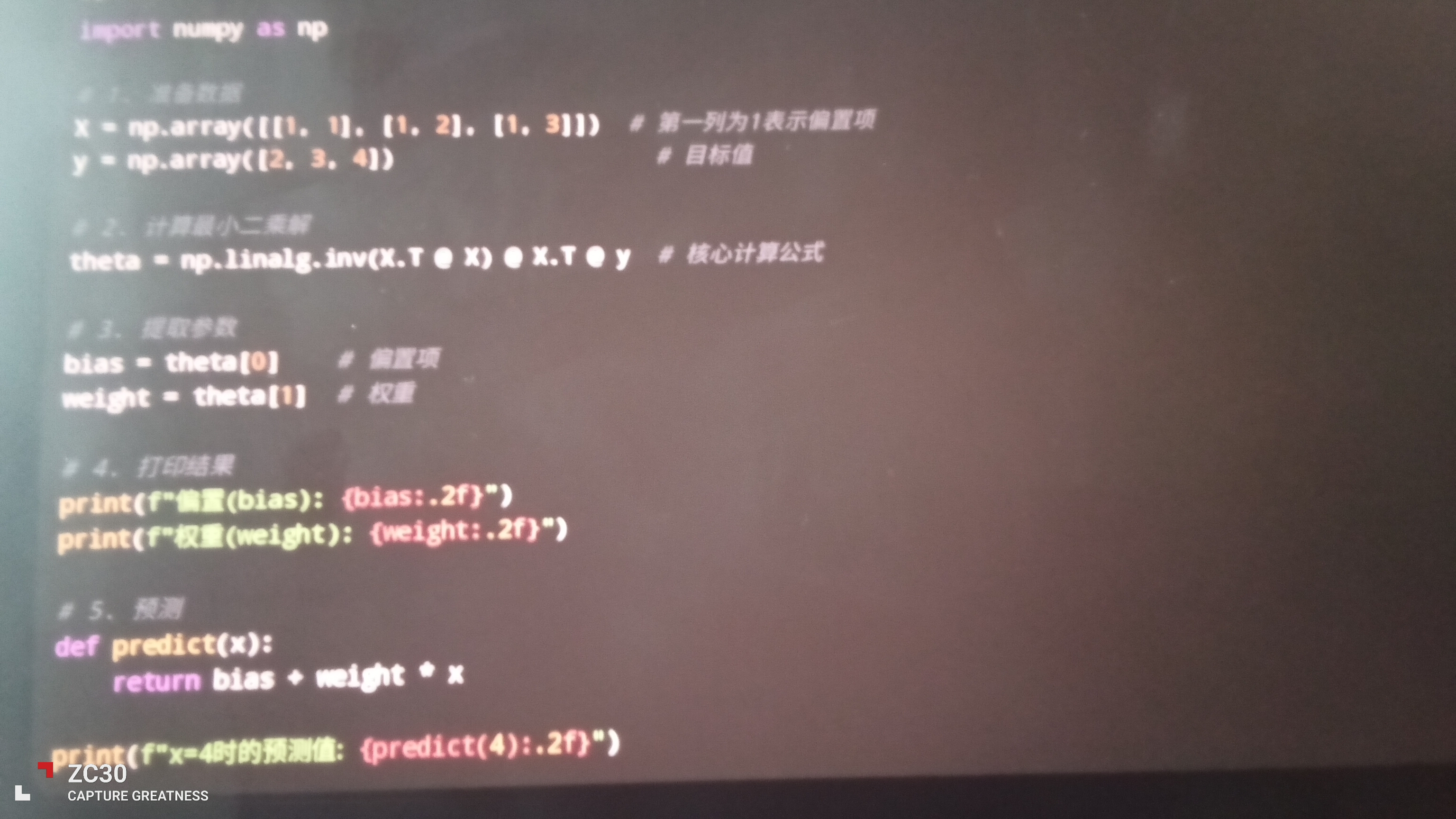
物理 线性回归-Python
import numpy as np
import pdb
from scipy import linalg
def LU_decomposition(A):
n = len(A[0])
L = np.zeros((n, n))
U = np.zeros((n, n))
for i in range(n):
L[i][i] = 1
if i == 0:
U[0][0] = A[0][0]
for j in range(1, n):
U[0][j] = A[0][j]
L[j][0] = A[j][0] / U[0][0]
else:
for j in range(i, n):
temp = 0
for k in range(0, i):
temp = temp + L[i][k] * U[k][j]
U[i][j] = A[i][j] - temp
for j in range(i + 1, n):
temp = 0
for k in range(0, i):
temp = temp + L[j][k] * U[k][i]
L[j][i] = (A[j][i] - temp) / U[i][i]
return L, U
def least_square(x, y):
"""
para X: 矩阵, 样本特征矩阵
para Y: 矩阵, 标签向量
return: 矩阵, 回归系数
"""
# 计算增广特征矩阵 X_tilde
one_temp = np.ones((len(x)))
one_temp = one_temp.reshape((len(x), 1))
X_tilde = np.c_[one_temp, X]
# 定义 A, b 的值
A = np.dot(X_tilde.T, X_tilde)
b = np.dot(X_tilde.T, y)
# 对矩阵 A 进行 LU 分解, 求 Aw = b
# 过程: A = LU, LE = b, Uw = I
L, U = LU_decomposition(A)
Z = linalg.solve(L, b)
w = linalg.solve(U, Z)
print("L=", L)
print("U=", U)
print("Z=", Z)
print("Exact solution: w=", w)
return w
X = [25, 40, 55, 80, 122, 135]
Y = [136, 140, 155, 160, 157, 175]
W = least_square(X, Y)
import matplotlib.pyplot as plt
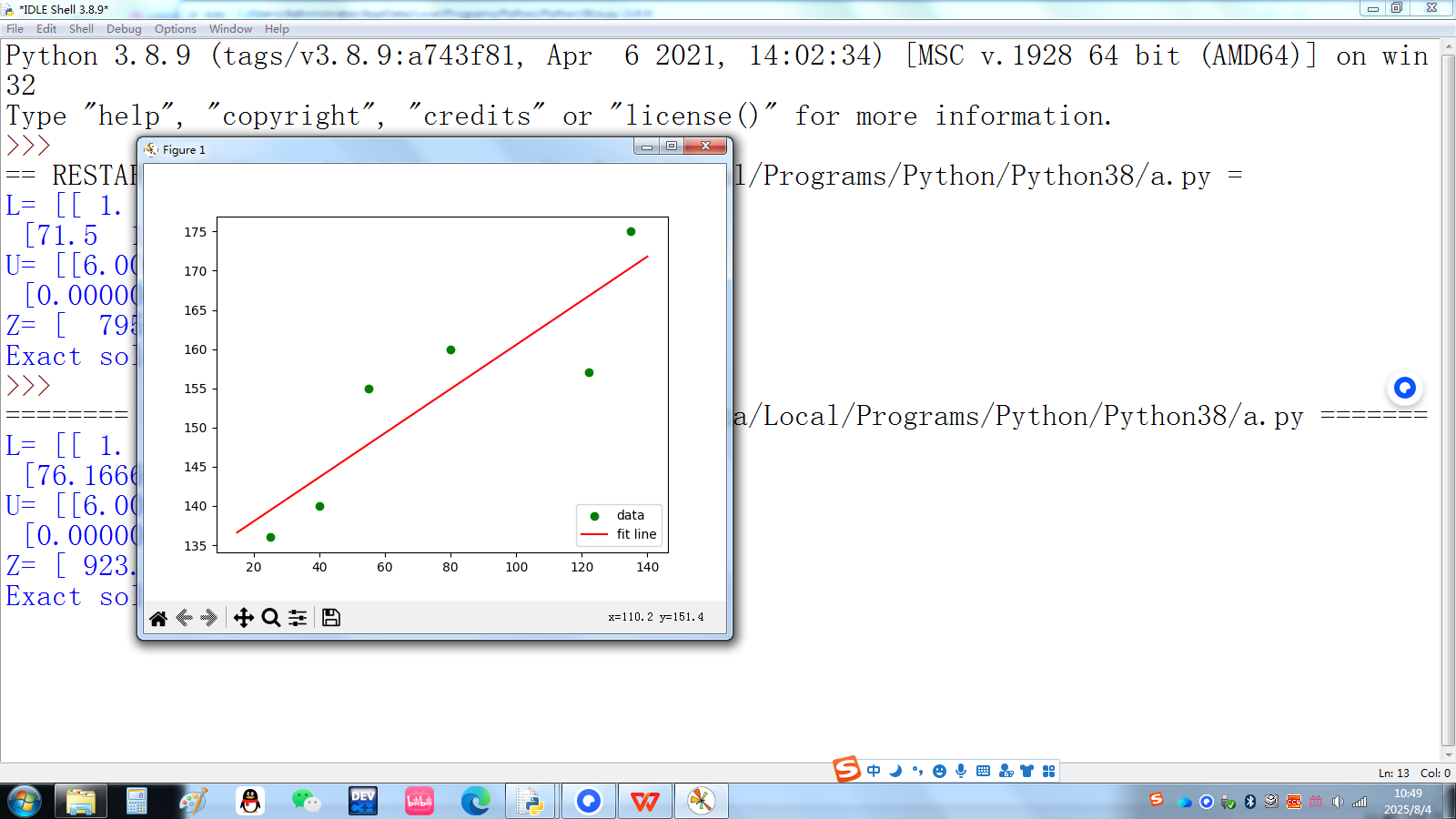
plt.scatter(X, Y, color="green", label="data")
x1 = np.linspace(15, 140, 100)
y1 = W[1] * x1 + W[0]
plt.plot(x1, y1, color="red", label="fit line")
plt.legend(loc='lower right')
plt.show()
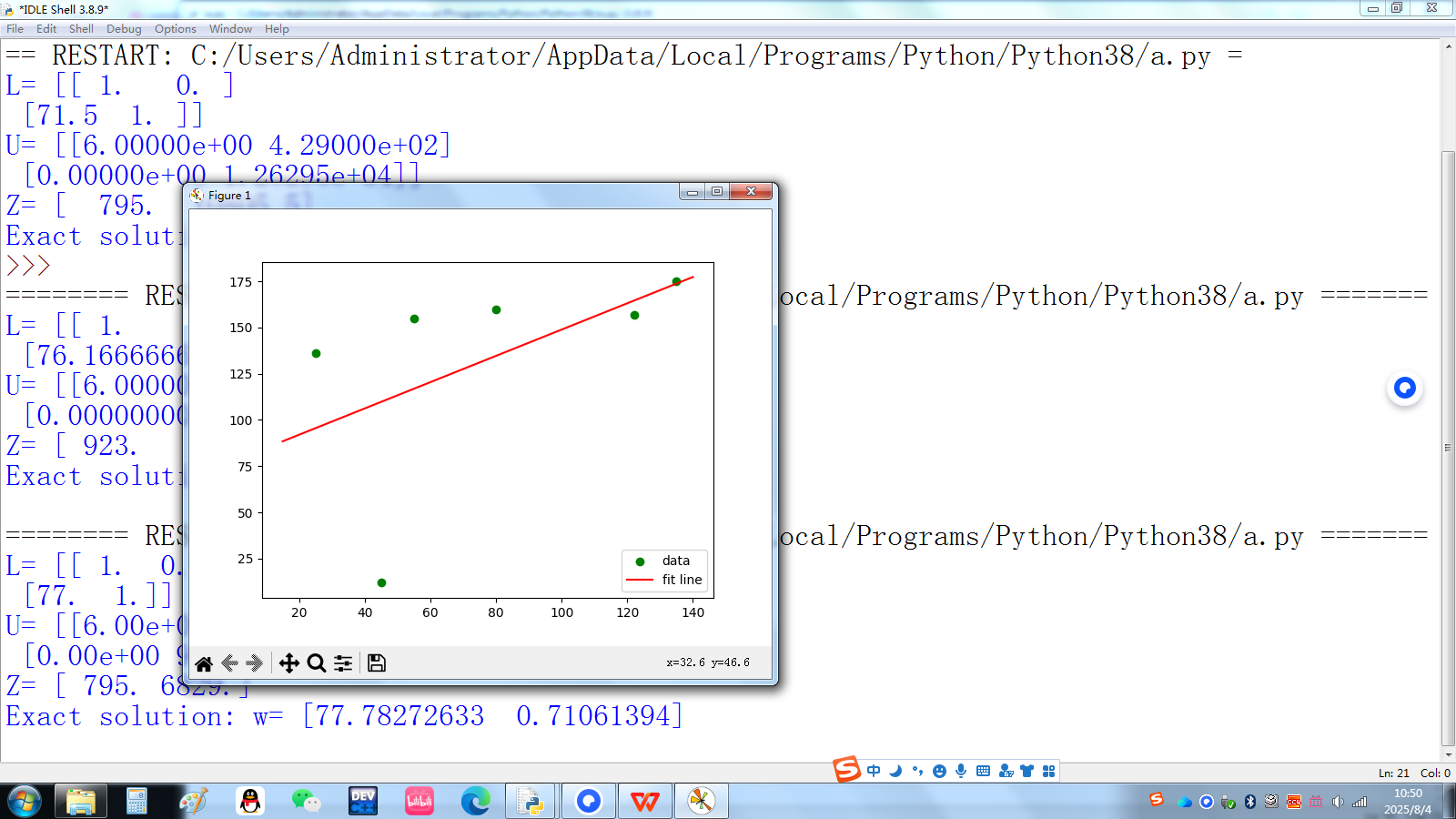
当数据中存在极为离谱的数据时会和原来的回归极为不同引发极为可怕的结果
共2条回复
时间正序