物理 [论坛资料室]专题:碰撞与圆周率
码字中…
让我们直入主题吧.
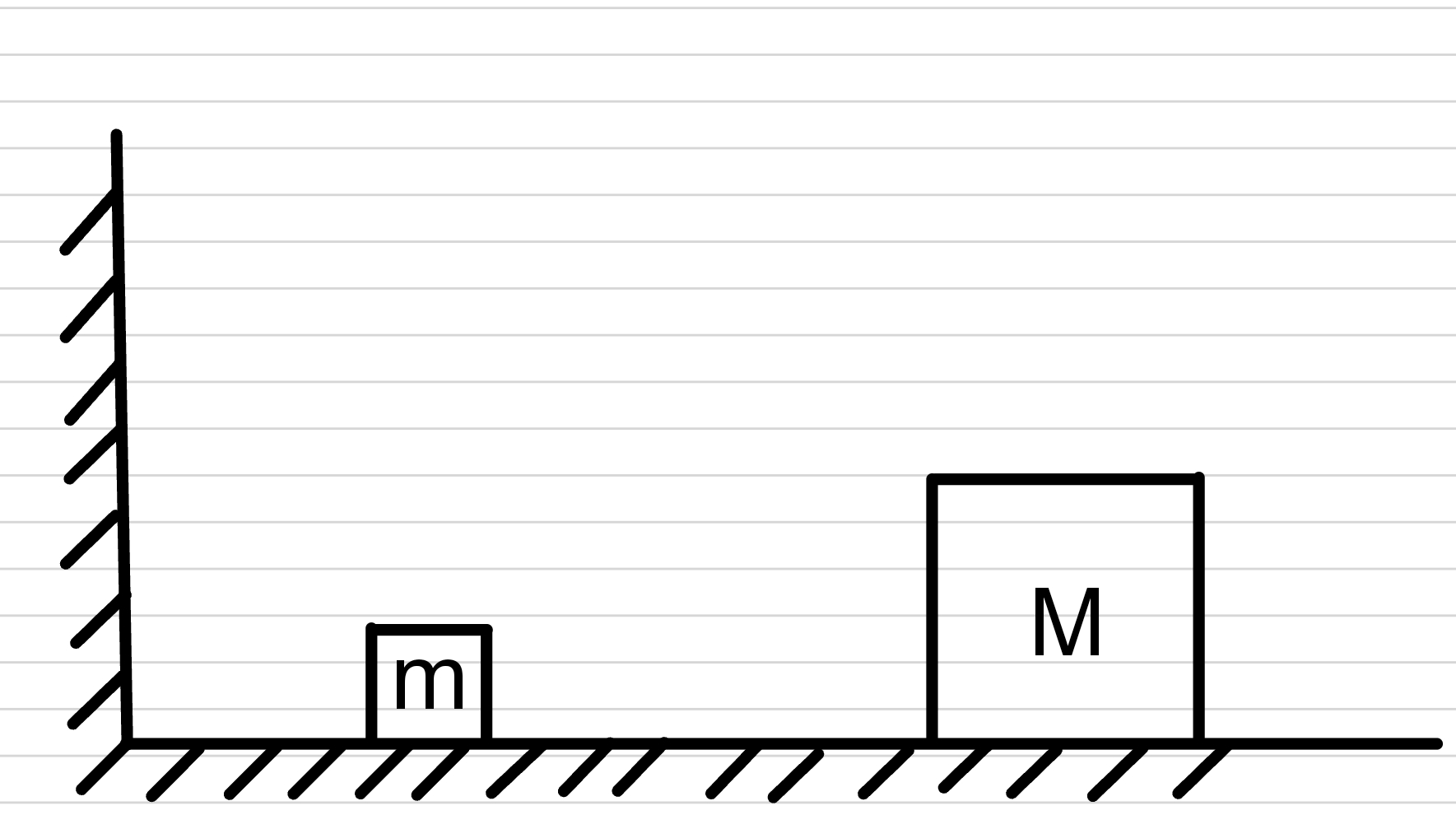
如图所示,在光滑地面上从左到右依次为固定挡板,质量为$m$的物体A和一质量为$M=km$的物体B.现给$M$一个初速度,假设所有碰撞均为弹性碰撞,将$m$与挡板的碰撞计入在内,求:
(1)当$k=1$时,总碰撞次数$N_1$;
(2)当$k=100$时,总碰撞次数$N_2$;
(3)当$k=10^2n$时,总碰撞次数$N_3$.
(1)瞪眼法出$N_1=3$.第一问纯送分;
(2)我们班的 物 竞 大 佬 已经开始列式了:
$v_m'=\frac{(m-M)v_m+2Mv_M}{m+M}$
$v_M'=\frac{(M-m)v_M+2mv_m}{m+M}$
然后就是代值求解和无脑迭代…如果你这么做了,说明你是个人物;如果你还做出来了,那么mol佬(♿
那么,真正精妙的做法是什么呢?我们先看到第三问.先列出能量和动量守恒:
$\frac{1}{2}mv_m^2+frac{1}{2}Mv_M^2=C_1$
$\mv_m+Mv_M=C_2$
特别注意$C_2$由于与挡板的碰撞会改变.
接下来我们可以画出$v_1—v_2$坐标,就会发现:能量守恒为一个椭圆,其方程为
$(\frac{v_m}{sqrt{frac{M}{m}v})^2+(frac{v_M}{v})^2=1$
而动量守恒为一条条斜率为$k$的直线
其中$k=—\frac{m}{M}$
$然而椭圆显然不方便计算,因此我们可以变换坐标系为\sqrt{M}v_m—sqrt{M}v_M坐标$
如此做,能量守恒的曲线为圆,如图。
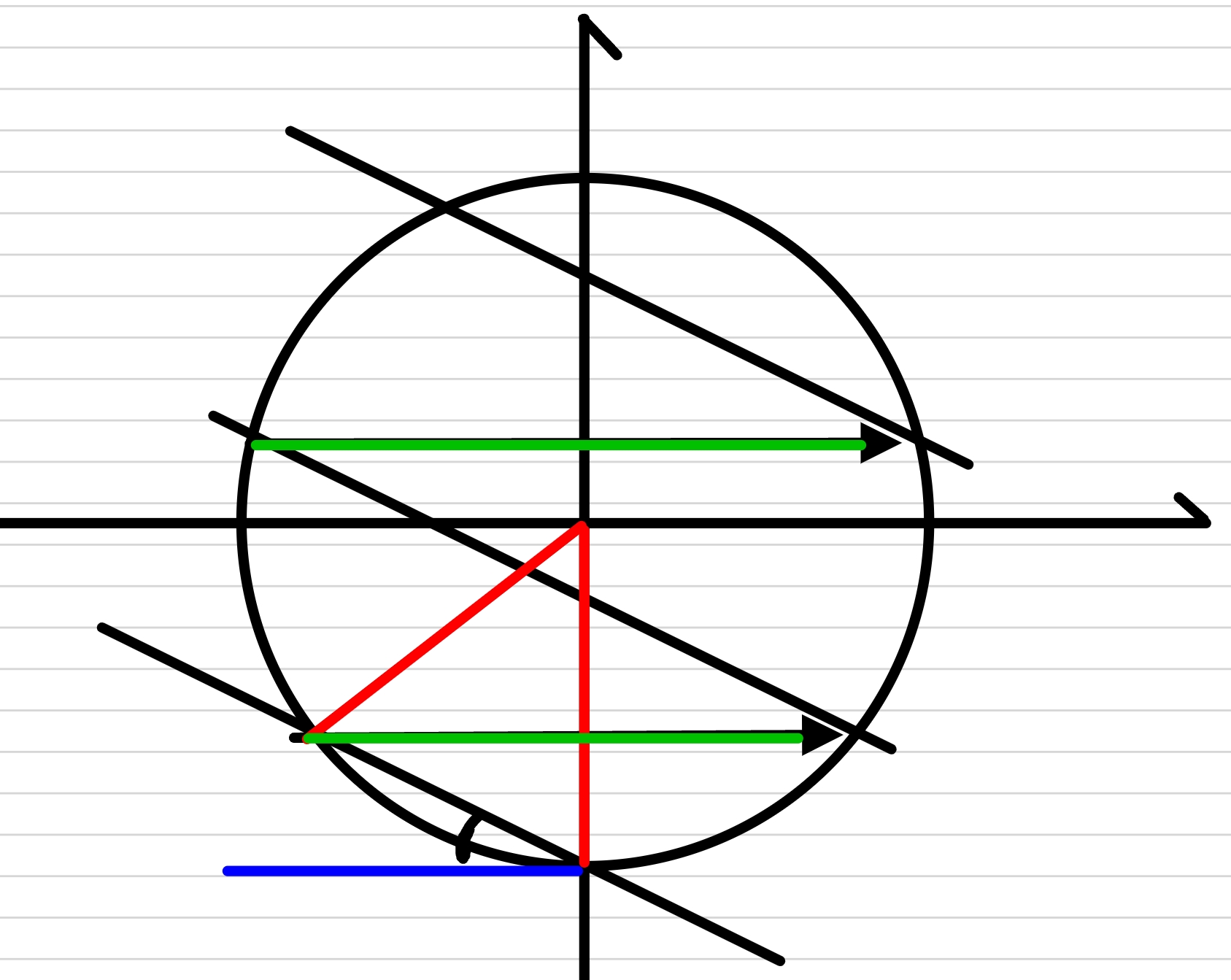
$初始坐标显然为(0,\sqrt{m}v)$
以此点画动量守恒直线,与圆另一交点即为第一次碰撞后的坐标。
$\由弦切角定理,圆心角 theta与弦切角 theta_0的关系为$
$\theta=2 theta_0$
共1条回复
时间正序
