物理

[论坛资料室]生物信息之信息学知识

简单说一下什么是动态规划

动态规划可以理解成一个矩阵，具体看下图：（手打的比较难看忍忍哈）

规则，从（0，0）走到＊号，走过的格子数值加起来最大，每个格子只能走一遍，只能向右或向下走，请问最大值是多少

那么我们可以通过动态规划解决这个问题，先简单思考一下吧

因为机器不像我们一样可以较为感性的判断大小，所以他得走完所有路径，那么从（0，0）到＊要走90（如果没算错的话）条路非常的麻烦

那么我们要如何解决这个问题呢，因为题目规定只能向右或下两个方向，所以我们就可以用双层循环即

外边是纵向循环，里面是横向循环（横向走完一圈纵向向下移动一格，横向重新从零开始

纵向循环是i从0到6，横向循环是j从0到5

我们可以根据数学知识推得动态转移方程

在我们i==0,j从0到5的时候，我们需要比较，上方的数字和左方的数字谁打，谁打就用大的加上[i][j]本身的数

川川也讲过这东西叫DP 数组（我就直接用这个名字了）

所以我们动态转移方程就是DP[i][j]=DP[i][j]+max(DP[i-1][j],DP[i][j-1]);//max是取最大值的意思

这样我们的这个数组处理好了，我们的＊号位就是最大值了

注意，因为在第一排和第一列的时候没有这个内存空间（你的数组方块就那么大，超出去是不可以的）

所以记得在i==1或j==1时做出特殊处理，现在，让我将转移后的数组画出，大家手动做一遍这个操作即可（我应该没算错）

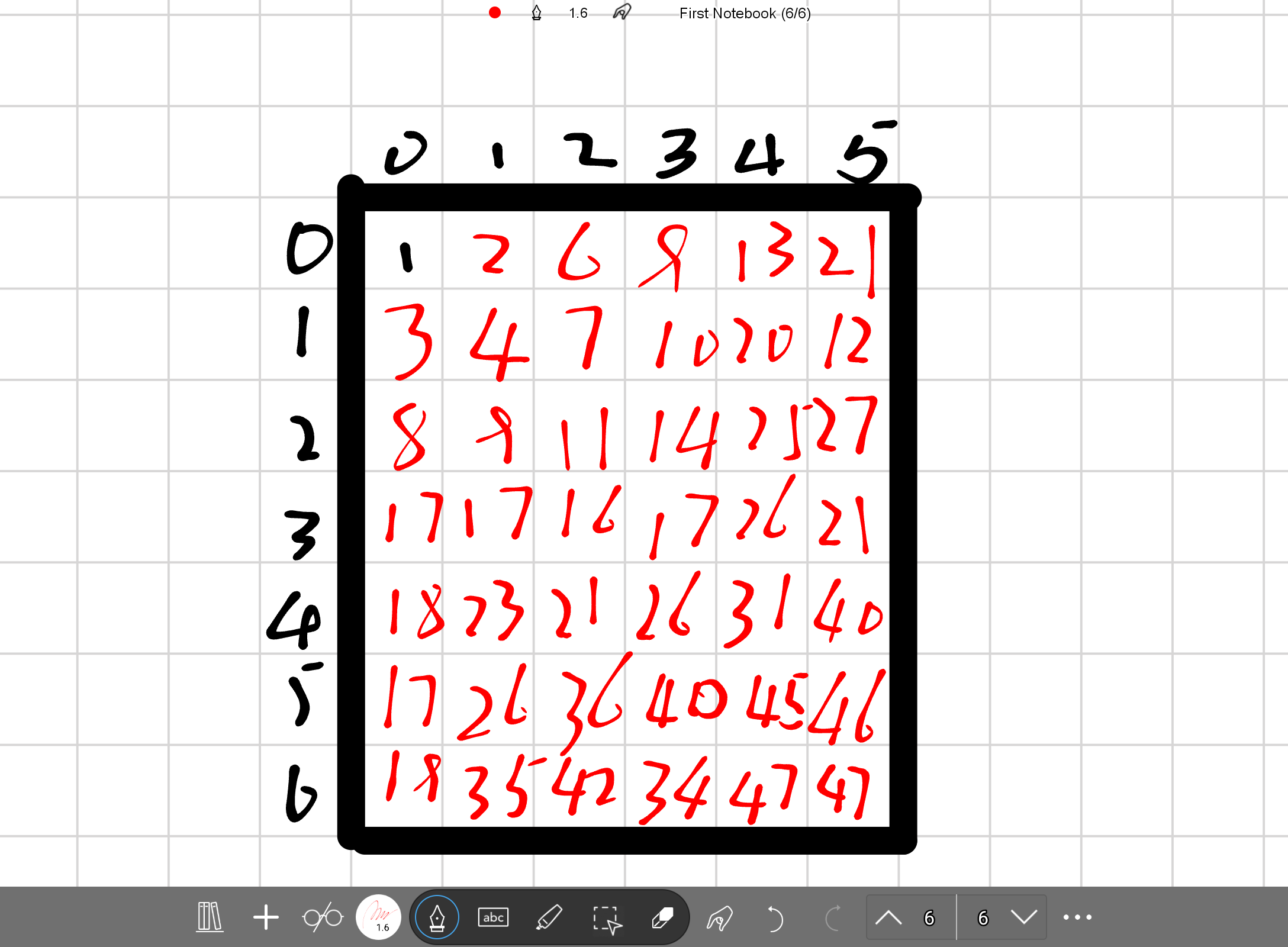
由于个人水平原因只能教到这里了，@柠檬味的小龙虾康康吧

所以答案是多少？@这个可以有

完结撒花，就这吗一点需要知道的，剩下的生信老师都会讲的

（完结的最快的知识帖哈哈哈哈）

统计的建树呢我没学明白（我不会说我的临接链表就是史的）

最后@柠檬味的小龙虾你自己过来学哈