物理

[论坛资料室]《拓扑原卷》其一

禁止沙发，禁止水评。

置顶：证明更完力，我需要来一个天才帮我做一个穿孔棱柱的折纸教程，或者帮我把那个对偶图Γ画出来，我需要看看它的圈和增厚后的样子。另：马上要说到映射，但我没有学，需要等我自学一下。

下周回来必须写完作业才能看板砖www。一切更新计划取消。等我高中就自由了😯.这几天的更新计划是今天更证明，下周更一个二级证明，四月底更出来最重要的同胚等价。目前帖内错误已改正。多面体有时候我会打成多边体，一个意思区别二维和三维就看是形还是体就够了。

                                                         $Huge{版权声明}$

参照教材是马克著的基础拓扑学，原作声明不可复制或抄袭原作任何部分，故此贴所有内容均为笔者所思考总结或询问他人说得经验组成，笔者[星空]享有全部版权，本文允许借鉴转运，复制请遵循CC协议(鞠躬)。由于作者学是浅薄，文本内容也会有些许错误，欢迎有见识的学者指出。

(出帖顺序及目录同原著)

(此贴为第一章      引论)

(所需图片来源，若为表明，均为原著所给)

$large{优美的Euler}$

       Euler定理极其证明是拓扑学中很多思想的根源(摘自原文)

       首先我们要清楚Euler定理是针对什么而定的，在拓扑学中，我们的主要研究对象是几何体，对于欧式几何，多边体是起最显著代表，你可以随手画一个正多边体，(四，六，八，十二)，或是任意一个凸多边体，你甚至可以随意拿起一个足球来数一数它的顶点数($v$)，棱数($e$)，数目($f$)，在这中，我们用$v-e+f$，即它的顶点数减去棱数加数目，那么你可以得到，这些多边体，这些结果都是2。  

        我们以正六边体为例，它的顶点数是8，棱长是12，数目（原作成为数目，据我理解应该就是面数，但应该两者是有不同的）是6。此时$v-e+f=8-12+6=2$这很容易， 事实上，我们生活中常见的多边体都满足这个规律，哪怕是让我等众生异常头疼的凹多边体也是如此。就比如这一张图（图后要写的话直接看图上吧，拓扑开始还算简单，我这种菜还能接受）

          那么，作为一名优秀的学者，你应该为这个命题产生些许怀疑了，针对任意一个命题，我们都应严格的去证明它的真实性，科学性，普遍性，唯一性。                            为找出反例，马克发挥了他的聪明才智，他找到了如下两张图

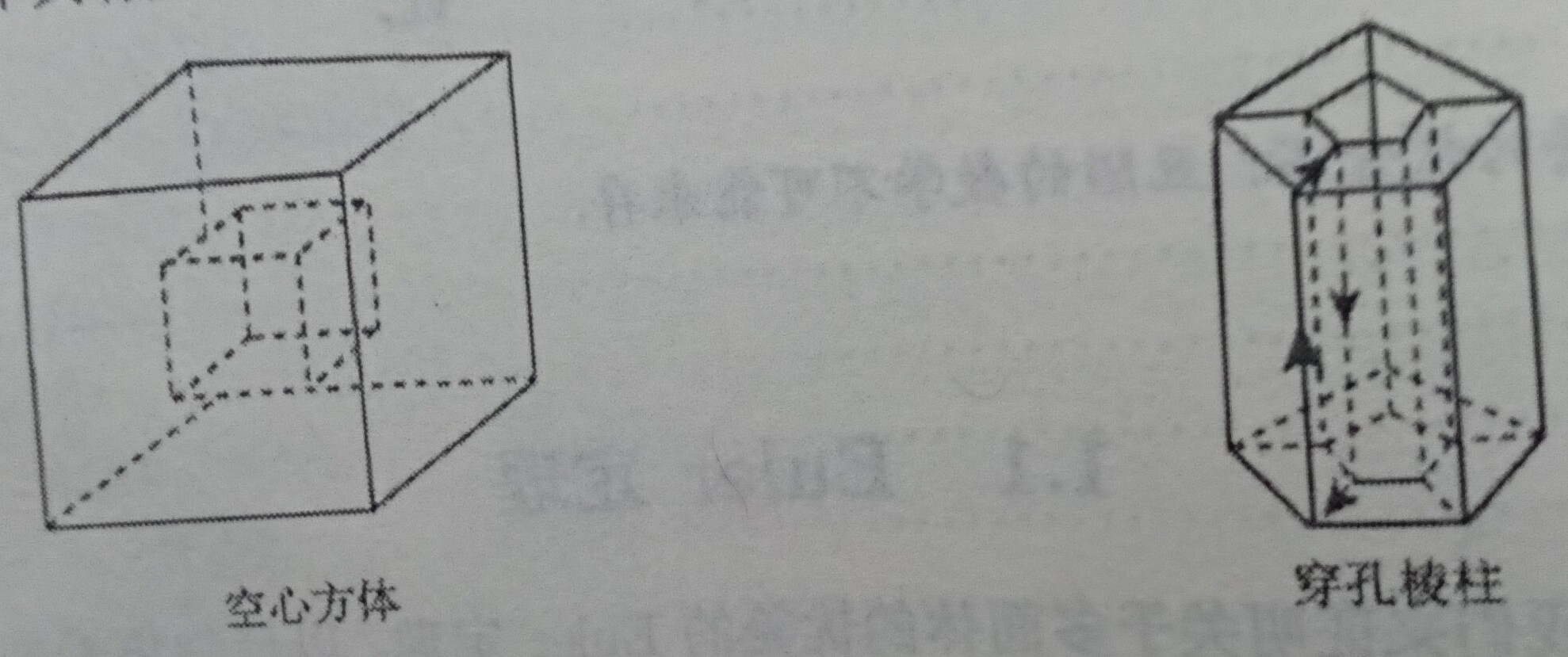分析一下左图(四维空间的常见图)的$vef$，可得$v=16$,$e=24$,$f=12$,so:$v-e+f=16-24=12=4$，此时的Euler为4而不是2，为什么会有这样的情况？事实上，这种情况可以看作两个正六边形的嵌套，那么他的v、e、f值都理应乘2，结果乘2也就合理了。分析右图我们得到的却又是另一个结果：$v-e+F=0$

是1什么1导致1了Euler的值发生了改变？我们可以观察一下，左图中的多面体的表面分开成两块，用专业术语来讲，这个表面不连通，有理由把这样的情况排除在外，因为这两块的每一块都将使$v-e+f=2$的值。但即使这样，也不能说明右图的情况，此时多面体的表面只有一整块。但它有一个重要方面与前面的例子不等同。我们可以在这个表面上找到一个圈，这个圈分割表面为两部分，有理由把这样的情况排除在外。（此为原著部分，毕竟涉及理论知识的部分不得不引用一下，但我不会完全照搬原文的。就比如说，我会把原作化简一下。来看刚才原文提到的右图，这个所谓的圈，我们把它用剪刀剪开，它会变成一个无圈的图形，这就不至于把它分成两块，事实上，剪开1后的特性就和一个普通的正方体一样）

       接下来我们就可以得到Euler定理的前提条件了。（此处引用属于国际公有知识版权）

       （1.1）Euler定理     设P为满足下列条件的正多面体：

1. $P的任何两个顶点可以用一串棱相连接$；
2. $P上任何由直线段（不一定是P的棱）构成的图，把P分割成两片$.

   (今日任务完成，明日更新Euler定理的证明，这同样是一个引用）

         前言：此证明中“对偶”一词可能存在理解错误，一切以人民电邮出版社的《基础拓扑学》为标准教材。此证明为von Staudt于1847年发表（上面对Euler定理的准确表述也是他的作品）

          证明提要：P的一组连通的顶点与棱叫一个图，连通的意思｛脚注:此内容会在原卷3里讲｝就是任意两个顶点都可以用图中的一串棱连接。不包括任何圈的图叫做树形（对于树形来说$v-e=1$因为树的英文是tree）所以我们以T来记树形，上面的性质则写作$v(T)-e(T)=1$

          ＃注释／思考：$如果P中存在任意两个顶点可以被一些连续的棱相连，它便被称为连通（注：此为完全充分条件），因而可以构成一个图，我们可以用图来表示三维空间内任何一组线接起来的有限多条线段。至于上文提及两次的圈你就可以理解成二维投影中的封闭图形，比如你把一个正六面体（事实上：只要是满足Euler定理条件的多面体都可以同胚成）放在纸面上，它就是一个点（或是一条线段）而你把上面那个穿孔棱柱放在二维平面上，它就是一个封闭的五边形，因此它是有圈的。对于这个圈的位置，我想应该可以通过在封闭的五边形上任意取一点，这一点断开后将破坏这个图形本身的封闭性，那么这个点在三维空间的还原位置就是那个圈（准确地讲应该是那个面的周边）。二维空间上，任意不封闭的线状图形，其节点数（即我们所说的顶点v）和线段数（即我们所说的棱数e）之差一定是1。而封闭图形这会存在公共点问题。$

        现在我们来继续证明：按Euler的条件1来看，P的全体顶点构成一个图。在P中可以找到含有全部顶点的树形（$毕竟P的任意两个顶点 都能够由一串棱相连接$).于是，我们选择一个树形T，它包含P的某些棱，但包含P的全体顶点。然后我们构造T的一种”对偶“对偶：是一个图，我们称之为Γ，它是按下述方式定义的一个图Γ。相应于P的每个面（f），我们给出Γ的一个顶点A‘（我忘了向量怎么打了，先用A’代替）。Γ的每两个顶点之间都有一条棱相连，，并且仅当他们相应的面在P内的公共棱不属于T。｝而我们在把Γ在P中表示出来时，它的棱必然也允许有一个曲折点。¹

        （依然是证明而非思考）通过此方式得到的Γ是联通从而是一个图。为什么？可以想象如果Γ的某两个顶点不能用棱相连，则它们必然被T内的一个圈分开。由于T是树形而不包括任何的圈，所以Γ是连通的。        通过此方式得到的Γ还是个树形。为什么？若Γ内有圈，按P的条件2，这个圈将把P分成两块，每一块将含有T的至少一个顶点 ，也就是说，这个圈使T不能连通，矛盾。因此Γ是树形。

           （你知道这是什么）由于任何树形的顶点数比棱数多1，于是我们得到关于T的$v(T)-e(T)=1$和关于Γ的$v(Γ)-e(Γ)=1$

                于是$v(T)-e(T)+v(Γ)F-e(Γ)=2$

               因为我们按对偶构造，那么就得到了$v(T)=V$,$e(T)+e(Γ)=e$,$v(Γ)=f$.

               所以$v-e+f=2$