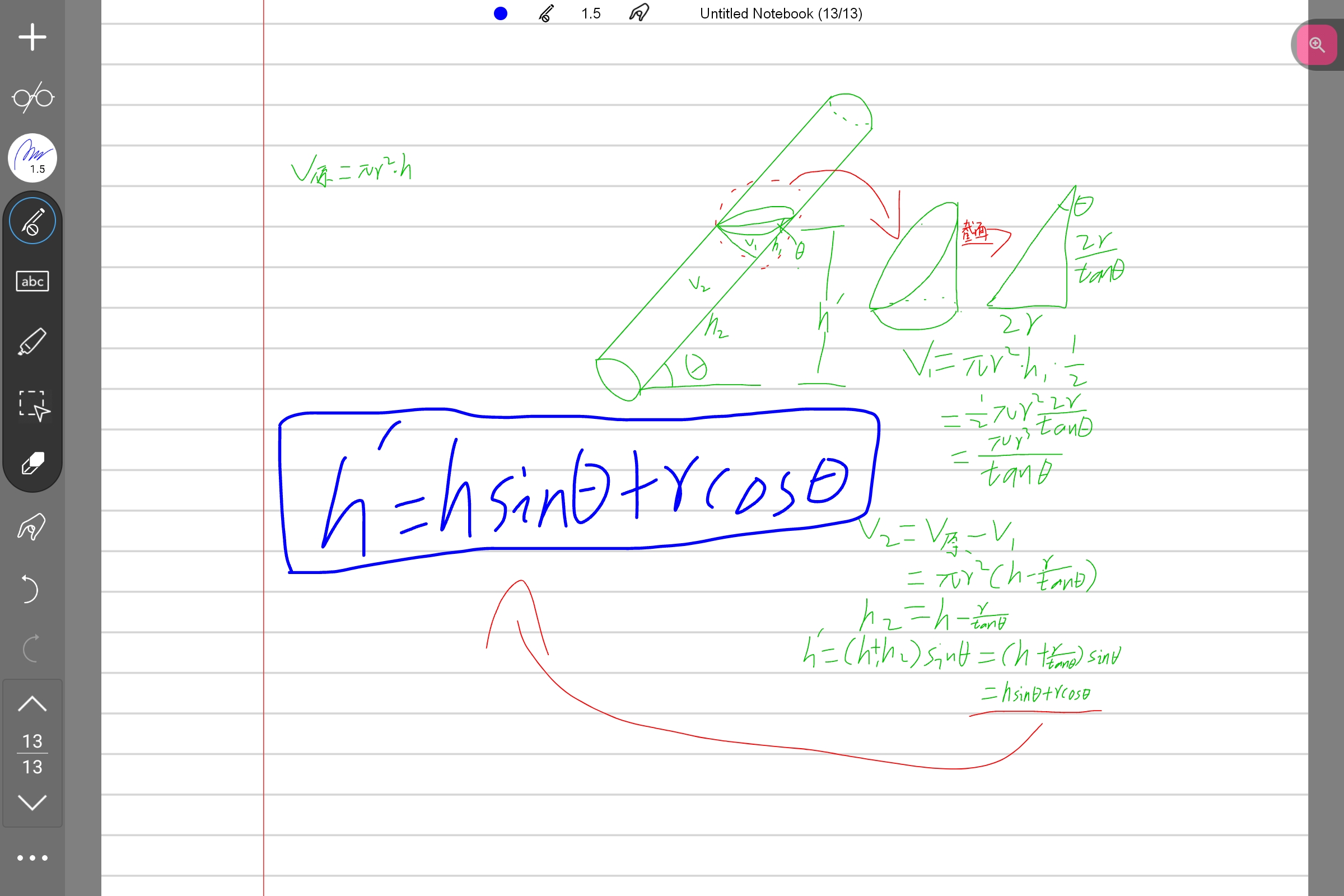
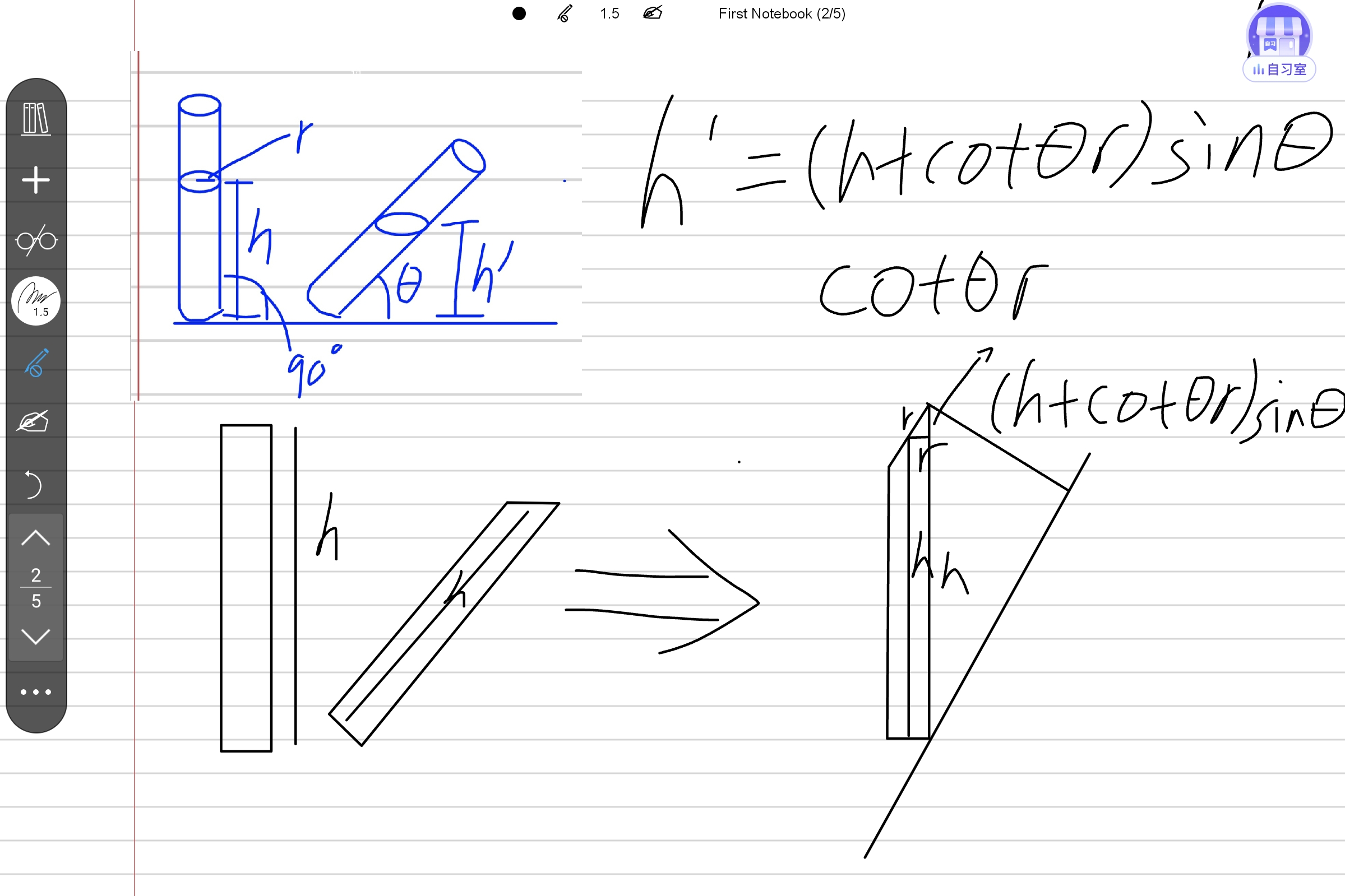
共44条回复
时间正序
- 时间正序
- 时间倒序
- 评论最多
1条评论 评论
- 1
4条评论 评论
7条评论 评论
Sorrowfulman.
3月前
4-4 23:31:02
其实你可以把上下限带进b和-b验算,如果是πab/2就没问题。
手积了一下,你第二项是不是少了个x...
2条评论 评论
3条评论 评论
世界是一个巨大的多醛基糖对吗(雾
2月前
5-4 12:49:29
你这个问题就和人为什么左胸腔有心脏而右胸腔没有一样…优美
当生物问题无法用科学解释时,我们往往会搬出万能的答案:because God…