物理

[论坛资料室]理论力学之欧拉-拉格朗日方程

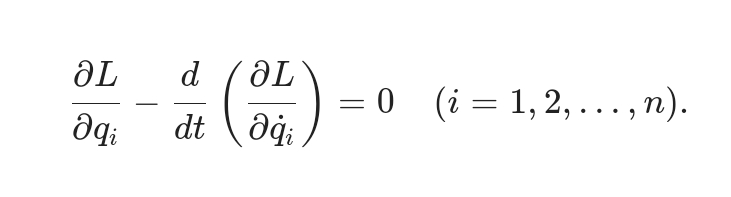
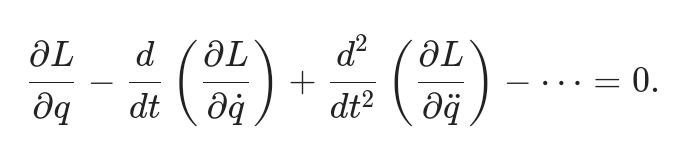
欧拉-拉格朗日方程（Euler-Lagrange Equation）是变分法中的核心方程，用于求解泛函的极值函数。它在物理学（如经典力学、场论）和工程学中具有广泛应用，尤其是从最小作用量原理推导系统的运动方程。以下从背景、推导、物理意义和应用进行详细介绍。

 一、问题背景：变分法与泛函极值泛函（Functional）是函数的函数，即输入为函数，输出为实数。例如，力学中的作用量S[q(t)]是路径 $ q(t) $ 的泛函。

目标：找到使泛函 $ J[q] = \int_{t_1}^{t_2} L(q, \dot{q}, t) \, dt $ 取极值的函数 $q(t)$，其中 $ L$ 为被积函数（拉格朗日量），$\dot{q} = dq/dt $。

二、欧拉-拉格朗日方程的推导

假设函数 $ q(t) $使泛函 $ J[q] $取得极值，考虑对其施加微小扰动 $ \delta q(t) $，并要求变分 $ \delta J = 0 $。

1. 变分的计算   引入扰动 $ q(t) \to q(t) + \epsilon \eta(t) $，其中 $ \eta(t) $ 是满足 $ \eta(t_1) = \eta(t_2) = 0 $的任意函数，$ \epsilon $为小参数。泛函的变分为：δ J = $ \frac{d}{d\epsilon} J[q + \epsilon \eta] |_{\epsilon=0} = \int_{t_1}^{t_2} \left( \frac{\partial L}{\partial q} \eta + \frac{\partial L}{\partial \dot{q}} \dot{\eta} \right) dt.$.

 2. 分部积分    对含 $ \dot{\eta} $的项分部积分，利用边界条件 $ \eta(t_1) = \eta(t_2) = 0 $：   $\int_{t_1}^{t_2} \frac{\partial L}{\partial \dot{q}} \dot{\eta} \, dt = \left. \frac{\partial L}{\partial \dot{q}} \eta \right|_{t_1}^{t_2} - \int_{t_1}^{t_2} \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) \eta \, dt. $  边界项消失后，变分简化为：    $\delta J = \int_{t_1}^{t_2} \left[ \frac{\partial L}{\partial q} - \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) \right] \eta(t) \, dt.$

3. 变分法基本引理    由于 $ \eta(t) $是任意的，极值条件 $\delta J = 0 $ 要求被积函数恒为零：      $\frac{\partial L}{\partial q} - \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) = 0.$  此即欧拉-拉格朗日方程。 

三、方程的推广形式

1. 多自由度系统    若系统有 $n$个广义坐标 $q_i(t)$，每个坐标对应一个方程：  $\frac{\partial L}{\partial q_i} - \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) = 0 \quad (i=1,2,\dots,n).$

2. 含高阶导数    若  $L$ 依赖 $q, \dot{q}, \ddot{q}, \dots$，方程为：   $\frac{\partial L}{\partial q} - \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}} \right) + \frac{d^2}{dt^2} \left( \frac{\partial L}{\partial \ddot{q}} \right) - \dots = 0.$

3. 显含时间变量     若 $L$ 显含时间 $t$，方程形式不变，但计算导数时需考虑 $t$ 的显式依赖。

 四、物理意义：最小作用量原理在经典力学中，系统的真实运动路径使作用量 $S = \int L \, dt$取极值。此时：拉格朗日量$L = T - V$，其中 $T$为动能，$V$ 为势能。- 欧拉-拉格朗日方程直接给出牛顿第二定律的广义坐标形式。

示例：自由粒子 拉格朗日量 $L = \frac{1}{2}m\dot{x}^2$，代入方程：$\frac{\partial L}{\partial x} - \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{x}} \right) = 0 - \frac{d}{dt}(m\dot{x}) = 0 \implies \ddot{x} = 0,$对应匀速直线运动。

五、应用领域

1. 经典力学：分析约束系统（如摆、刚体）。

2. 场论：导出麦克斯韦方程、爱因斯坦场方程等。

3. 最优控制：求解最优路径或资源配置问题。

4. 几何光学：通过费马原理推导光线传播路径。

六、历史背景

欧拉（1744年）首次提出该方程的一般形式。

拉格朗日（1755年）完善并推广至多自由度系统，奠定了分析力学的基础。

七、数学补充

必要条件：极值函数需满足二阶可微，且满足固定端点条件。

自然边界条件：若端点可变，需额外条件如 $\frac{\partial L}{\partial \dot{q}} \bigg|_{t_1, t_2} = 0$。

八、总结

欧拉-拉格朗日方程将物理系统的动力学问题转化为寻找泛函极值的数学问题，统一了力学与变分法，成为理论物理和工程建模的重要工具。其核心思想是通过局部微分条件刻画全局极值行为，体现了自然界的优化原理。

九、作者观点：嘿嘿嘿，力学题拉就完了！！！