物理

材料力学二进宫（2）

1. 让我们首先从猜想开始，为啥拉长橡皮泥，其直径变细了呢？实验结果证明，横向应变和轴向应变之比是一个常数，我们叫做泊松比，这里注意泊松比是个负数，和上次说的弹性模量E一样，这也是个固有的弹性常数。

2. 接下来不是知识点了，是个解法～叫做超静定问题！就是方程数量少于未知力的数量（什么居然又个名字hhhhh）为了解决这类问题，物竞里面咱们常说的”数学关系“，其实就叫做变形协调方程，给一题看看呢？

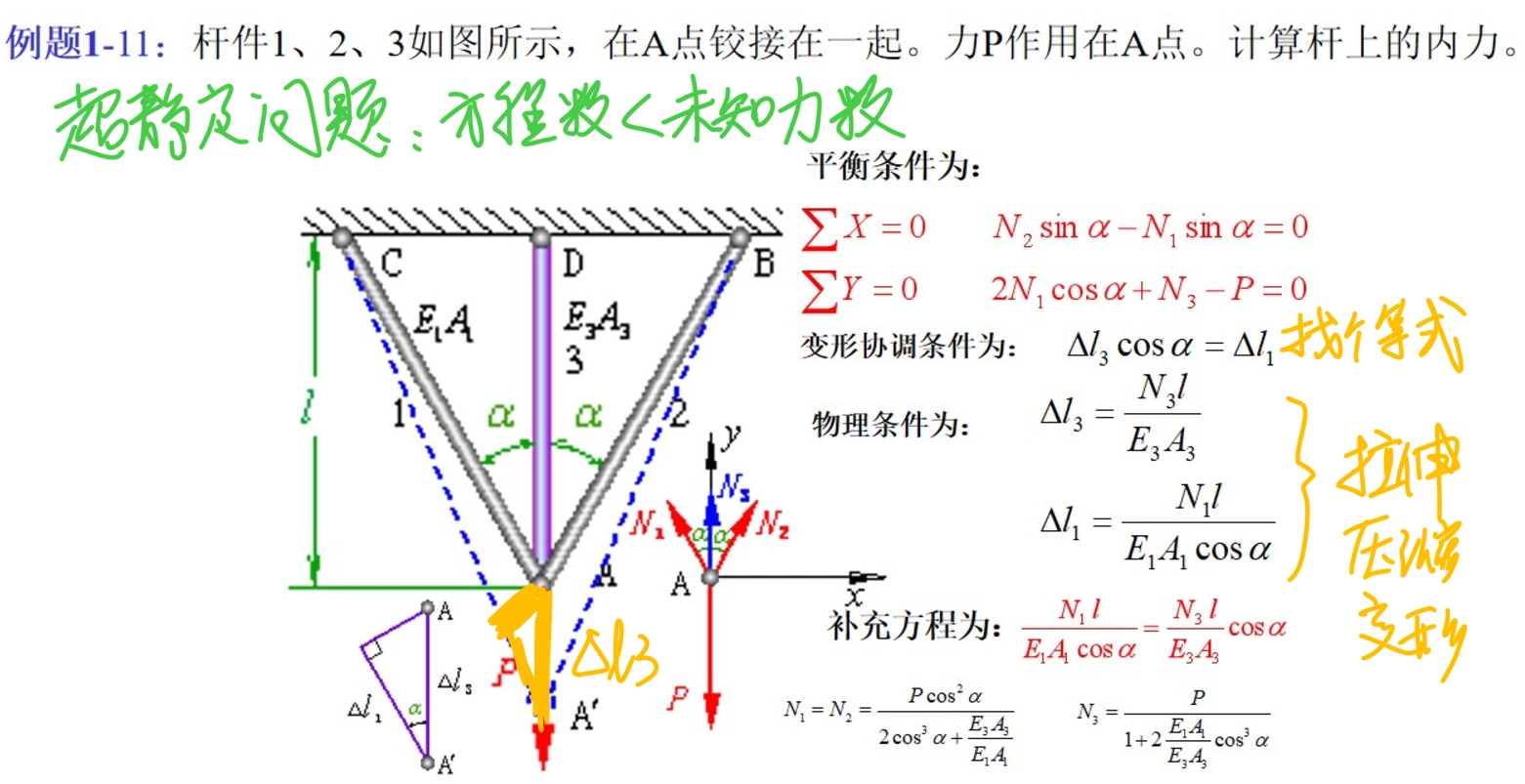
非常简单，记得上次有个同学提到虚功的问题https://forum.eduzhixin.com/discuss-detail/50786?tabSource&subjectType=2，其实就是找潜在的力的关系！差了个$pi $，当时想的是要沿着环积分来着？也不知道咋回事

3. 这章的$^{} $好玩之处在于扭转，这次不推导切应变的微分关系了，我们进行一波类比——应变和应力之间靠一个模量联系，这里也是，切应力=切应变*剪切弹性模量。可是在工程中，咱们往往好奇材料能坚持多少的扭矩，上回说到应力定义为$sigma $ = $rac{N（表面压力）}{A（表面面积）} $，力和面垂直才有力。，那么显然扭矩和应变之间，应该有一个面积项（聪明的你肯定能猜出这是ds）模仿转动惯量，这里定义极惯性矩（截面二次极矩）是$int $R$^{2} $ *ds，大家只要知道这是个常数，要算，和半径有关，会算转动惯量就会算极惯性矩（截面二次极矩）就ok

总结和预告——不妨想想你现在要弄断一支粉笔（大家下课可以顺三根粉笔试试）如果你拉断了他，就是上次说的拉伸；你扭断他，就是这次说的扭转；直接掰断，就是剪切（其实第一次也说了？），下一次，咱们说说弯曲时，其内力和变形～